
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Вариант №1
1) Построить эмпирическую функцию распределения
| Di | 3 - 6 | 6 - 9 | 9 - 12 | 12 - 15 | 15 - 18 | 18 - 21 |
| i |
2) Группа социологов исследовала влияние стажа работы по профессии на производительность труда рабочих механического цеха некоторого завода. Получены следующие результаты:
 |
| Источник изменчивости Результативный признак k | Стаж работы | ||
| до 10 лет | от 10 лет до 15 лет | от 15 лет до 20 лет | |
| Количество деталей, вырабатываемых за смену одним рабочим, шт. | – – | – |
Предполагая, что производительность труда рабочих, имеющих различный стаж работы, имеет нормальное распределение: Xi Î N (a i ;s i) (i= 1,2,3), причем  . Требуется проверить методом дисперсионного анализа нулевую гипотезу Н 0: а 1= а 2 = а 3 (средняя производительность труда не зависит от стажа работы). Уровень значимости a примем равным 0,05.
. Требуется проверить методом дисперсионного анализа нулевую гипотезу Н 0: а 1= а 2 = а 3 (средняя производительность труда не зависит от стажа работы). Уровень значимости a примем равным 0,05.
3)Найти  , S2, S1
, S2, S1
| xi | |||||
| mi |
4) В условиях примера 3 найти доверительный интервал для среднеквадратического отклонения при g = 0,95.
5) При проверке гипотезы о виде распределения  , число степеней свободы n = 9, уровень значимости a = 0,05. Можно ли считать гипотезу принятой?
, число степеней свободы n = 9, уровень значимости a = 0,05. Можно ли считать гипотезу принятой?
Решение.
1) Составим интервальный статистический ряд относительных частот (у нас n =60)

| 3-6 | 6-9 | 9-12 | 12-15 | 15-18 | 18-21 |

| 0,25 | 0,08 | 0,22 | 0,12 | 0,20 | 0,13 |
Для построения графика эмпирической функции распределения F*(x) найдем сначала ее аналитическое выражение. Для этого вместо интервального ряда будем рассматривать сгруппированный ряд и в качестве xi будем брать середины интервалов. Тогда по формуле (10) имеем:

Построим график функции F*(x). Здесь удобно взять разный масштаб на осях координат:
 F*(x)
F*(x)
 |

 1
1

 0,8
0,8

 0,6
0,6

 0,4
0,4








 0,2
0,2
 x
x
0 4,5 7,5 10,5 13,5 16,5 19,5
Рисунок 4
2) Согласно условию, нулевая и альтернативная гипотезы имеют вид:
Н 0: а 1= а 2 = а 3 – производительность труда не зависит от стажа работы;
На: производительность труда зависит от стажа работы.
Вычислим вспомогательные величины, необходимые для определения факторной и остаточной дисперсии: n =n 1 + n 2 + n 3 = 3 + 4 + 5 = 12.
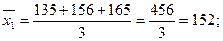


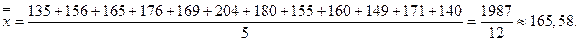
Таким образом, факторная дисперсия равна
 .
.
Остаточная дисперсия равна
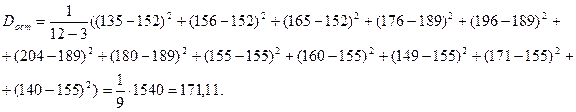
Вычислив F набл., получим

Найдем по таблицам квантилей F – распределения критическое значение F (a, v 1, v 2), соответствующее уровню значимости a = 0,05 и числам степеней свободы v 1= k – 1=2 и v 2 = n – k= 9. Это значение равно F (0,05; 2; 9) = 4,26. Так как Fнабл= 9,66 >4,26, то нулевая гипотеза отвергается, т.е. считается статистически доказанным, что производительность труда зависит от стажа работы.
3) Найдем числовые характеристики реализации выборки.  можно найти по формуле (1), однако здесь удобнее воспользоваться формулой:
можно найти по формуле (1), однако здесь удобнее воспользоваться формулой:

т.к.  =100, имеем,
=100, имеем,
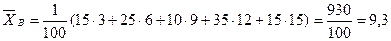
Для вычисления  можно воспользоваться формулой (2), но удобнее ее находить по формуле:
можно воспользоваться формулой (2), но удобнее ее находить по формуле:

имеем:
 Для определения
Для определения  необходимо сначала найти
необходимо сначала найти  - несмещенную выборочную дисперсию. Она отличается от дисперсии выборки
- несмещенную выборочную дисперсию. Она отличается от дисперсии выборки  (или иначе
(или иначе  ) только множителем
) только множителем 

Тогда:
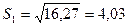
4) Доверительный интервал для среднеквадратического отклонения будем искать используя (8), найдем по таблице приложения 4 при γ = 0,95 и n = 100 значение q(γ,n), получим q(0,95; 100)=0,143. Тогда
S1(1 - q) = 4,03(1 - 0,143) = 3,46
S1(1 + q) = 4,03(1 + 0,143) = 4,61
Доверительным интервалом будет (3,46, 4,61).
5) Проверим гипотезу о виде распределения. По заданным уровню значимости α и числу степеней свободы ν найдем по таблице критических точек распределения χ2 значение χ20,05;9= 16,9. По условию χ2набл= 18,4. У нас χ2набл > χ2табл, следовательно, гипотеза о виде распределения отвергается.
Вариант № 2
1) Построить гистограмму относительных частот, выдвинуть гипотезу о виде распределения
| Δi | 0 - 2 | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 | 10 - 12 | 12 -14 |
| mi |
2) Найти  , DB, S1
, DB, S1
| xi | ||||||
| mi |
3) Получить уравнение линейной регрессии, сделать чертеж
| xi | ||||||
| yi |
4) В условиях примера 2 найти доверительный интервал для математического ожидания при неизвестном  ,
, 
5) При проверке гипотезы о показательном распределении  , число разрядов 9, уровень значимости
, число разрядов 9, уровень значимости  . Можно ли считать гипотезу принятой?
. Можно ли считать гипотезу принятой?
Решение.
1) Преобразуем статистический ряд частот в ряд относительных частот. У нас  , имеем
, имеем

| 0 - 2 | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 | 10 - 12 | 12-14 |

| 0,35 | 0,25 | 0,13 | 0,12 | 0, 10 | 0,02 | 0,03 |

| 0,175 | 0,125 | 0,065 | 0,06 | 0,05 | 0,01 | 0,015 |
Введем систему координат с разными масштабами на осях. Отложим 7 частичных интервалов с длинами  на оси OX и построим на них как на основаниях прямоугольники с высотами
на оси OX и построим на них как на основаниях прямоугольники с высотами  (см. рисунок 5).
(см. рисунок 5).





0,16

 0,12
0,12

 0,08
0,08
 |
0,04
 |
0 2 4 6 8 10 12 14 
Рисунок 5
По виду гистограммы выдвигаем гипотезу о том, что СВХ распределена по показательному закону (см. рисунок 2).
2) Найдем  (см. вариант 1)
(см. вариант 1)
 =
=  (
( =
=
=  (40 + 120 + 195 + 540 + 600 + 480)=19,75
(40 + 120 + 195 + 540 + 600 + 480)=19,75
 =
=  [8 (5 - 19,75)2 + 12 (10 - 19,75)2 + 13 (15-19,75)2 +
[8 (5 - 19,75)2 + 12 (10 - 19,75)2 + 13 (15-19,75)2 +
+ 27 (20 - 19,75)2 + 24 (25 - 19,75)2 + 16 (30 - 19,75)2]=
=  (1740,5 + 1140,75 + 293,31 + 1,69 + 661,5 + 1681,0) = 55,19
(1740,5 + 1140,75 + 293,31 + 1,69 + 661,5 + 1681,0) = 55,19
Для определения  сначала найдем несмещенную выборочную дисперсию
сначала найдем несмещенную выборочную дисперсию 

тогда 
4) Уравнение линейной регрессии имеет вид

Для определения коэффициентов  и
и  надо решить систему уравнений (15). Суммы, входящие в эту систему, удобно вычислять в специальной таблице:
надо решить систему уравнений (15). Суммы, входящие в эту систему, удобно вычислять в специальной таблице:
| xi | yi | xi2 | xiyi |
В последней строке стоят нужные нам суммы. Подставляя в систему, получим

Решим эту систему методом Крамера
 =330-225=105
=330-225=105  0,
0,
следовательно система уравнений имеет единственное решение.
 =495-135=360
=495-135=360
 =54-135=-81
=54-135=-81
 ,
, 
Следовательно, эмпирическое уравнение регрессии имеет вид

Построим корреляционное поле и график этого уравнения (рисунок 6)

Рисунок 6
Видим, что график уравнения достаточно хорошо описывает экспериментальные данные.
4) Предполагая, что СВ Х распределена по нормальному закону для определения доверительного интервала воспользуемся выражением (7)
У нас  ,
,  ,
,  ,
, 
Величину  найдем по таблице приложения 3 руководства /3/, имеем
найдем по таблице приложения 3 руководства /3/, имеем

Тогда доверительный интервал имеет вид

или, после вычислений (17,79; 21,71).
5) При проверке гипотезы о виде распределения надо сравнить полученное по формуле (11) значение  с табличным значением
с табличным значением  . Значение
. Значение  дано в условии задачи.
дано в условии задачи.
Для определения по таблице  надо знать уровень значимости
надо знать уровень значимости  и число степеней свободы ν.
и число степеней свободы ν.
Уровень значимости  по условию задачи равен 0,01. Число степеней свободы найдем по формуле
по условию задачи равен 0,01. Число степеней свободы найдем по формуле
ν = k–r-1
Число интервалов  по условию равно 9, у показательного распределения один параметр, значит
по условию равно 9, у показательного распределения один параметр, значит  .
.
Тогда ν =9 – 1 - 1 или ν = 7.
Найдем  по таблице критических точек распределения
по таблице критических точек распределения  , в руководстве /3/ это таблица ПРИЛОЖЕНИЕ 5, имеем
, в руководстве /3/ это таблица ПРИЛОЖЕНИЕ 5, имеем  . У нас
. У нас  , следовательно, гипотеза о показательном распределении принимается.
, следовательно, гипотеза о показательном распределении принимается.
Не нашли, что искали? Воспользуйтесь поиском: