
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Система с одним сервером
В первом столбце таблицы 4 показаны формулы для определения некоторых параметров системы с одним сервером, которая подчиняется модели M/G/1. В соответствии с этой моделью скорость поступления элементов данных подчиняется пуассоновскому закону, а время обслуживания - нормальному распределению. Использование масштабирующего коэффициента А в значительной мере упрощает формулы для вычисления основных выходных параметров. Следует учесть, что коэффициент масштабирования зависит только от отношения стандартного (среднеквадратичного) отклонения времени обслуживания к среднему времени обслуживания. При этом не требуется никакой другой информации о времени обслуживания.
Другие два случая, разобранные в таблице 4, это - модель с распределением времени ожидания по пуассоновскому закону, а времени обслуживания - по экспоненциальному закону (М/М/1, второй столбец) и модель, в которой время обслуживания всех элементов одинаково (а значит, отклонение времени обслуживания равно нулю), а время поступления элементов подчиняется пуассоновскому закону (M/D/1, третий столбец в таблице 14.1). Как уже отмечалось, вычисления при помощи этих формул носят приближенный характер, но для практического применения их точности вполне достаточно.
Таблица 14.1 - Используемые параметры
| Символ | Описание |
| l | Средняя скорость поступления элементов данных в систему (число элементов в секунду) |
| Ts | Среднее время обслуживания поступивших элементов (в секундах) |
| s Ts | Стандартное отклонение во времени обслуживания элемента (в секундах) |
| r | Утилизация сервера при обслуживании (доля времени, когда сервер занят) |
| U | Интенсивность графика |
| Q | Общее количество элементов данных в системе |
| Q | Среднее количество элементов данных в системе |
| ТQ | Время, которое элементы данных проводят в системе (в секундах) |
| Tq | Среднее время, которое элементы данных проводят в системе (в секундах) |
| sq | Стандартное отклонение q |
| sTq | Стандартное отклонение Tq (в секундах) |
| w | Среднее количество элементов данных, ожидающих обслуживания в очереди (размер очереди) |
| Тw | Среднее время, которое элементы данных ожидают обслуживания (в секундах) |
| Td | Среднее время ожидания обслуживания для элементов данных, находившихся в очереди (то есть, не включая элементы, для которых время ожидания равно 0) |
| sw | Стандартное отклонение w |
| N | Число серверов |
| m x(r) | х меньше или равно m x(r) в r процентах случаев |
Практика показывает, что наихудшую производительность демонстрирует система с экспоненциальным распределением времени обслуживания, а наилучшую производительность - система с постоянным временем обслуживания (что, впрочем, неудивительно). Поэтому обычно можно рассматривать систему с экспоненциальным распределением времени обслуживания как систему с худшими параметрами.
Эти же рассуждения применимы при рассмотрении различных распределений времени поступления элементов данных (то есть различного характера варьирования скорости прихода данных в систему). Для скорости поступления элементов, подчиняющейся пуассоновскому распределению, время между поступлениями элементов изменяется по формуле Пуассона и коэффициент стандартного отклонения от среднего равен единице.
Таблица 14.1 - Формулы для определения параметров системы с одним сервером
| Модель с нормальным распределением времени обслуживания (M/G/1) | Модель с экспоненциальным распределением времени обслуживания (М/М/1) | Модель с постоянным временем обслуживания (M/D/1) |

| 
| 
|

| 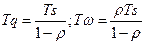
| 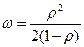
|

| 
| 
|
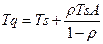
| 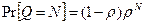
| 
|
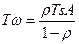
| 
| 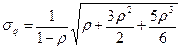
|

| 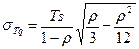
| |
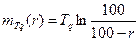
| ||

|
Если наблюдаемый коэффициент меньше единицы, то скорость поступления элементов постоянна. В этом случае применение предположения о пуассоновском распределении скорости поступления даст завышенную оценку размера очереди и задержек в ней. С другой стороны, если коэффициент больше единицы, то перегрузка системы в этом случае становится более вероятной.
Рассмотренная теория очередей достаточно эффективно может быть использована на практике в различных ситуациях. Приведем пример практического применения теории очередей. Рассмотрим локальную сеть, имеющую в своем составе 100 рабочих станций и один сервер (N = 1), который обслуживает общую базу данных. Среднее время ответа сервера на запрос – 0,6 с. Стандартное отклонение этого времени также равно 0,6 с. В пиковые периоды работы локальной сети скорость поступления запросов к серверу достигает значения 20 запросов в минуту.
При расчете нас будут интересовать следующие вопросы:
- Чему равно среднее время ответа сервера?
- Если время ответа, равное 1,5 с, рассматривается как максимально приемлемое, то насколько может вырасти процент загрузки до достижения насыщения сервера?
- Если ожидается, скажем, 20-процентное увеличение утилизации сервера, то насколько увеличится время ответа (на 20 %, больше чем 20 %, меньше чем 20 %)?
Предположим, что в рассматриваемой ситуации применима модель М/М/1. Будем игнорировать задержки, вносимые сетью, полагая, что распределение задержки в ней можно не принимать в расчет.
Вычислим некоторые параметры сети. Сначала найдем скорость поступления l:
l = 20 поступлений в минуту = 20/60 поступлений в секунду = 1/3 поступлений в секунду.
Утилизация сервера вычисляется по формуле
r = l Ts/N = (1/3 поступлений в секунду) (0,6 с на передачу)/1 = 0,2.
Вычислим среднее время ответа:

На второй вопрос однозначно ответить сложно, так как существует ненулевая вероятность того, что в некоторых случаях время ответа сервера будет превышать 1,5 с. Поэтому можно предположить, что в 90 % ответы сервера будут даны менее чем за 1,5 с. Если сделать такое допущение, то мы сможем воспользоваться формулой

Получаем:
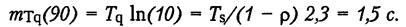
Учитывая, что Ts = 0,6 с, получаем утилизацию сервера r = 0,08, то есть 8 %. Итак, можно сказать, что при изменении загруженности сервера в диапазоне от 8 до 20 % (см. выше) время ответа сервера будет менее 1,5 с в 90 % случаев.
В заключение определим зависимость между возрастанием нагрузки и увеличением времени ответа. Время ответа будет увеличиваться несколько медленнее, чем утилизация. Действительно, в нашем случае, если утилизация сервера возросла с 20 до 40 % то значение Tq изменится от 0,75 с до 1,0 с (как нетрудно подсчитать), что означает увеличение на 33,3 %.
Задание на работу
1 Ознакомиться с теоретическим материалом.
2 Изучить методику расчета.
3 Выполнить расчет согласно индивидуальному заданию (табл. 14.3).
4 Проанализировать полученные результаты и сделать вывод.
5 Рассмотреть параметры, влияющие на окончательные результаты.
6 Оформить отчет и подготовиться к защите работы.
Не нашли, что искали? Воспользуйтесь поиском: