
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лекция 6. Анализ и синтез информационных систем. 9 страница
6. Для каждого символа ch' в алфавите выполняем сортировку элементов V, начинающихся с ch, за которым следует ch'. В процессе выполнения сортировки сравниваем элементы Y путем сопоставления суффиксов, которые они представляют при индексировании массива W. На каждом шаге рекурсии следует отслеживать число символов, которые оказались равными в группе, чтобы не сравнивать их снова. Все суффиксы, начинающиеся с ch, отсортированы в рамках V.
7. Для каждого элемента V[i], соответствующего суффиксу, начинающемуся с ch (то есть, для которого S[V[i]] = ch), установить W[V[i]] значение с ch в старших битах и i в младших битах. Новое значение W[V[i]] сортируется в те же позиции, что и старые значения.
Данный алгоритм может быть улучшен различными способами. Одним из самоочевидных методов является выбор символа ch на этапе 5, начиная с наименьшего общего символа в S и предшествующий наиболее общему.
Ссылки
1. M.Buirows and D.J.Wheeler. A block-sorting Lossless Data Compression Algorithm Digital Systems Research Center. SRC report 124. May 10, 1994.
2. J.L.Bently, D.D.Sleator, R.E.Tarjan, and V.K.Wei. A locally adaptive data compression algorithm. Communications of the ACM, Vol. 29, No. 4, April 1986, pp. 320- 330
3. E.M.McCreight. A space economical suffix tree construction algorithm. Journal of the ACM, Val. 32, No. 2, April 1976, pp. 262-272.
4. U.Manber and E.W.Mayers, Suffix arrays: Anew method for on-line string searches. SIAM Journal on Computing, Vol. 22, No. 5, October 1993, pp. 935-948.
12.3 Сжатие данных с использованием преобразования Барроуза-Вилера
Майкл Барроуз и Давид Вилер (Burrows-Wheeler) в 1994 году предложили свой алгоритм преобразования (BWT). Этот алгоритм работает с блоками данных и обеспечивает эффективное сжатие без потери информации. В результате преобразования блок данных имеет туже длину, но друтой порядок расположения символов. Алгоритм тем эффективнее, чем больший блок данных преобразуется (например, 256-512 Кбайт). Пояснение работы алгоритма будет выполнено на ограниченном объеме исходных данных (строка S длиной N, например, SEMENOV). Строка S рассматривается как последовательность, состоящая из N строк.
Сначала осуществляется циклический сдвиг строки S и формируется N-1 новая строка. На практике строки не размножаются, а создается массив указателей на циклический буфер, где лежит исходная строка S.
| Строка | |
| S EMENOY | SO |
| EMENOYS | SI |
| MENOYSE | S2 |
| ENOYSEM | S3 |
| NOYSEME | S4 |
| ОYSEMEN | S5 |
| YSEMENO | S 6 |
Далее выполняется лексикографическое упорядочение (сортировка) этих строк (указателей). Для упорядочения можно использовать С-функции типа strcmp() или memcmp() (учитывая особенности структуры буфера, это должны быть их функциональные аналоги).
| F | L | Строка | |||||
| E | M | E | N | О | Y | S | SI |
| E | N | О | Y | s | E | M | S3 |
| M | E | N | О | Y | S | E | S2 |
| N | О | Y | s | E | M | E | S4 |
| О | Y | S | E | M | E | N | S5 |
| s | E | M | E | N | О | Y | SO |
| Y | S | E | M | E | N | О | S 6 |
Первая колонка помечена буквой F, а последняя - L. Колонка F (EEMNOSV) содержит все символы исходной строки S, записанные в упорядоченной последовательности. Строка L представляет собой последовательность префиксных символов для строки S.
Результатом работы алгоритма BWT является строка L и первичный индекс, который представляет собой номер элемента строки L, где хранится первый символ исходной строки S. В приведенном примере индекс равен 1.
Лекция 13. Метод Шеннона-Фано
Данный метод выделяется своей простотой. Берутся исходные сообщения m(i) и их вероятности появления P(m(i)). Этот список делится на две группы с примерно равной интегральной вероятностью. Каждому сообщению из группы 1 присваивается 0 в качестве первой цифры кода. Сообщениям из второй группы ставятся в соответствие коды, начинающиеся с 1. Каждая из этих групп делится на две аналогичным образом и добавляется еще одна цифра кода. Процесс продолжается до тех пор, пока не будут получены группы, содержащие лишь одно сообщение. Каждому сообщению в результате будет присвоен код х с длиной -lg(P(x)). Это справедливо, если возможно деление на подгруппы с совершенно равной суммарной вероятностью. Если же это невозможно, некоторые коды будут иметь длину —lg(P(x))+l. Алгоритм Шеннона-Фано не гарантирует оптимального кодирования. Смотри http:/AvwwjcsAici.edu/^darL/pubs/DC-Sec3-html.
13.1 Статический алгоритм Хафмана
Статический алгоритм Хафмана можно считать классическим (см. также Р. Галлагер. Теория информации и надежная связь. "Советское радио", Москва, 1974.) Определение
статический в данном случае относится к используемым словарям. Смотри также www.ics.ics.uci.edu/~dan/pubs/DataCompression.html (Debra A. Lelewer и Daniel S. Hirschberg).
Пусть сообщения m(l),...,m(n) имеют вероятности P(m(l)),... P(m(n)) и пусть для определенности они упорядочены так, что P(m(l)) i Р(т(2)) i... i P(m(N)). Пусть xl,..., xn - совокупность двоичных кодов и пусть 11, 12,..., IN - длины этих кодов. Задачей алгоритма является установление соответствия между m(i) и xj. Можно показать, что для любого ансамбля сообщений с полным числом более 2 существует двоичный код, в котором два наименее вероятных кода xN и xN-1 имеют одну и ту же длину и отличаются лишь последним символом: xN имеет последний бит 1, a xN-1 - 0. Редуцированный ансамбль будет иметь свои два наименее вероятные сообщения сгруппированными вместе. После этого можно получить новый редуцированный ансамбль и так далее. Процедура может быть продолжена до тех пор, пока в очередном ансамбле не останется только два сообщения. Процедура реализации алгоритма сводится к следующему (см. рис. 2.6.5.1). Сначала группируются два наименее вероятные сообщения, предпоследнему сообщению ставится в соответствие код с младшим битом, равным нулю, а последнему - код с единичным младшим битом (на рисунке т(4) и т(5)). Вероятности этих двух сообщений складываются, после чего ищутся два наименее вероятные сообщения во вновь полученном ансамбле (т(3) и т(4); p(rrf (4)) = р(т(4)) + Р(т(5))).
| Код | С ообшвнив -«.■www —| w.... w | P(m(i)) |
| m(1) | 0.3 | |
| m(2) | 0,25 | |
| m(3) | 0,25 | |
| m(4) | 0.1 | |
| m(5) | 0.1 | |
| E = | 1.0 |
| 0.55 |
| А 1 |
| 0.45 |
Зис. 2.6.5.1 Пример реализации алгоритма Хафмана
На следующем шаге наименее вероятными сообщениями окажутся т(1) и т(2). Кодовые слова на полученном дереве считываются справа налево. Алгоритм выдает оптимальный код (минимальная избыточность).
При использовании кодирования по схеме Хафмана надо вместе с закодированным текстом передать соответствующий алфавит. При передаче больших фрагментов избыточность, сопряженная с этим не может быть значительной.
Возможно применение стандартных алфавитов (кодовых таблиц) для пересылки английского, русского, французского и т.д. текстов, программных текстов на С++, Паскале и т.д. Кодирование при этом не будет оптимальным, но исключается статистическая обработка пересылаемых фрагментов и отпадает необходимость пересылки кодовых таблиц
13.2 JPEG.
Формат файла JPEG (Joint Photographic Experts Group - Объединенная экспертная группа по фотографии, произносится "джейпег") был разработан компанией C-Cube Microsystems как эффективный метод хранения изображений с большой глубиной цвета, например, получаемых при сканировании фотографий с многочисленными едва уловимыми (а иногда и неуловимыми) оттенками цвета. Самое большое отличие формата JPEG от друтих рассмотренных здесь форматов состоит в том, что в JPEG используется алгоритм сжатия с потерями (а не алгоритм без потерь) информации. Алгоритм сжатия без потерь так сохраняет информацию об изображении, что распакованное изображение в точности соответствует оригиналу. При сжатии с потерями приносится в жертву часть информации об изображении, чтобы достичь большего коэффициента сжатия. Распакованное изображение JPEG редко
соответствует оригиналу абсолютно точно, но очень часто эти различия столь незначительны, что их едва можно (если вообще можно) обнаружить.
Процесс сжатия изображения JPEG достаточно сложен и часто для достижения приемлемой производительности требует специальной аппаратуры. Вначале изображение разбивается на квадратные блоки со стороной размером 8 пикселов. Затем производится сжатие каждого блока отдельно за три шага. На первом шаге с помощью формулы дискретного ко синусоидально го преобразования фуры (DCT) производится преобразование блока 8x8 с информацией о пикселах в матрицу 8x8 амплитудных значений, отражающих различные частоты (скорости изменения цвета) в изображении. На втором шаге значения матрицы амплитуд делятся на значения матрицы квантования, которая смещена так, чтобы отфильтровать амплитуды, незначительно влияющие на общий вид изображения. На третьем и последнем шаге квантованная матрица амплитуд сжимается с использованием алгоритма сжатия без потерь.
Оперирует алгоритм областями 8x8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого, при разложении матрицы такой области в двойной ряд по косинусам значимыми оказываются только первые коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет малой величины значений амплитуд высоких частот в реальных изображениях.
Поскольку в квантованной матрице отсутствует значительная доля высокочастотной информации, имеющейся в исходной матрице, первая часто сжимается до половины своего первоначального размера или даже еще больше. Реальные фотографические изображения часто совсем невозможно сжать с помощью методов сжатия без потерь, поэтому 50%-ное сжатие следует признать достаточно хорошим. С друтой стороны, применяя методы сжатия без потерь, можно сжимать некоторые изображения на 90%. Такие изображения плохо подходят для сжатия методом JPEG.
При сжатии методом JPEG потери информации происходят на втором шаге процесса. Чем больше значения в матрице квантования, тем больше отбрасывается информации из изображения и тем более плотно сжимается изображение. Компромисс состоит в том, что более высокие значения квантования приводят к худшему качеству изображения. При формировании изображения JPEG пользователь устанавливает показатель качества, величине которого "управляет" значениями матрицы квантования. Оптимальные показатели качества, обеспечивающие лучший баланс между коэффициентом сжатия и качеством изображения, различны для разных изображений и обычно могут быть найдены только методом проб и ошибок.
Коэффициент архивации в JPEG может изменяться в пределах от 2 до 200 раз. Как и у любого друтого алгоритма сжатия с потерями, у JPEG свои особенности. Наиболее известны "эффект Гиббса" и дробление изображения на квадраты 8x8. Первый проявляется около резких границ предметов, образуя своеобразный "ореол". Он хорошо заметен, если, допустим, поверх фотографии сделать надпись цветом, сильно отличающимся от фона. Разбиение на квадраты происходит, когда задается слишком большой коэффициент архивации для данной конкретной картинки.
Не очень приятным свойством JPEG является также то, что нередко горизонтальные и вертикальные полосы на дисплее абсолютно не видны, и могут проявиться только при печати в виде муарового узора. Он возникает при наложении наклонного растра печати на полосы изображения. Из-за этих сюрпризов JPEG не рекомендуется активно использовать в полиграфии, задавая высокие коэффициенты. Однако при архивации изображений, предназначенных для просмотра человеком, он на данный момент незаменим.
Широкое применение JPEG сдерживается, пожалуй, лишь тем, что он оперирует 24- битными изображениями. Поэтому для того, чтобы с приемлемым качеством посмотреть картинку на обычном мониторе в 256-цветной палитре, требуется применение соответствующих алгоритмов и, следовательно, определенное время. В приложениях, ориентированных на придирчивого пользователя, таких, например, как игры, подобные задержки неприемлемы. Кроме того, если имеющиеся у вас изображения, допустим, в 8- битном формате GIF перевести в 24-битный JPEG, а потом обратно в GIF для просмотра, то
 определяются
определяются
|
Последовательность нулей и кодовым вектором, Свойство линейного кода дает вектор, алгебраическую группу по они являются групповыми ко расстояние между кодовых.
его
вектора, полученного в результате образом:, для данного группового кода. Гру р аз м: е рн о сть к о то рых число столбцов равно +=: (71) Коды, коды, где _ а соответствующие
образующими. Порождающая матрица С может быть матрицы И равно: (72) Т
| с другой стороны, сумматоров по модулю 2 в П, тем: сложнее аппаратура.. Вес каждой: строки: вес соответствующей строки матрицы И. Если: |
| любую |
удобно брать единичную матрицу в При выборе матрицы П исходят из разрядах проверочной матрицы 11, тем ближе соответствующий
П определяет
диниц в матрице П должен быть не м:енее, где» И - единичная, то (удобство ^ t ^ жшшось бы как
| коду, будем (разность) кодовых векторов коду. Линейные коды образуют Свойство группового кода: минимальное кодовое группового кода равно минимальному весу |


| векторами равно весу по модулю 2. Таким коды удобно задавать матрицами, кода и:, Число строк матрицы: |

матрицу группового кода можно привести к следующему
Для кодов с =2
 Во
Для кодов с всех кодов с порождаемому коду
корректирующих.
Во
Для кодов с всех кодов с порождаемому коду
корректирующих.
|
разрядов, либо максимальная простота аппаратуры. Корректирующие коды с минимальным количеством: избыточных разрядов называют плотно упакованными или совершенным:» кодами. Для кодов с соотношения и и:, следующие: (3: 1), (7;4), (1.5; 11), (31; 26), (63; 57) и т. д. Плотно упакованные коды, оптимальные с точки зрения минимума избыточных символов, обнаруживающие максимально возможное количество вариантов ошибок кратностью г + 1; г 4- 2 и т, д. и имеющие и, были исследованы Д. Слепяном в работе [10]. Для получения этих кодов матрица П должна иметь комбинации с максимальным весом. Для этого при: построении: кодов с последовательно используются: векторы: длиной п, весом. Тем: же Слепяном в работе [11] были исследованы неплотно упакованные коды с малой плотностью проверок на четность, Эти коды экономны с точки зрения простоты аппаратуры и содержат минимальное число единиц в корректирующих разрядах порождающей матрицы- При построении: кодов с максимально простыми шифраторами и дешифраторами: последовательно выбираются векторы весом: 2, 3,, Если число комбинаций, представляющих собой корректирующие разряды кода и удовлетворяющих условию, больше, то в первом: случае не используют наборы с наименьшим весом, а во втором - с наибольшим. Строчки образующей матрицы С представляют собой комбинаций искомого кода. Остальные комбинации кода строятся при помощи образующей матрицы по следующему правилу: корректирующие символы, предназначенные для обнаружения: или исправления: ошибки в информационной части кода, находятся: путем суммирования по модулю 2 тех строк матрицы П, номера которых, совпадают с номерами разрядов, содержащих единицы: в кодовом векторе, представляющем информационную часть кода.. Полученную комбинацию приписывают справа к информационной части кода, и получают вектор полного корректирующего кода. Аналогичную процедуру проделывают со второй, третьей: и последующими информационными кодовыми комбинациями, пока не будет построен корректирующий код для передачи всех символов первичного алфавита. Алгоритм образования проверочных символов по известной информационной части: кода может быть записан следующим образом:
В процессе декодирования осуществляются проверки, идея, которых в общем виде может быть представлена следующим: образом::
Для каждой конкретной матрицы существует своя, од на-единствен пая: система проверок, Проверки производятся по следующему правилу: в первую проверку вместе с проверочным разрядом входят информационные разряды, которые соответствуют единицам первого столбца проверочной матрицы П; во вторую проверку входит второй проверочный разряд и информационные разряды, соответствующие единицам второго столбца проверочной матрицы, и т. д. Число проверок равно числу проверочных разрядов корректирующего кода, В результате осуществления проверок образуется: проверочный: вектор, который называют синдромом. Если вес синдрома равен нулю, то принятая комбинация считается безошибочной. Если хотя бы один разряд проверочного вектора содержит единицу, го принятая комбинация, содержит ошибку. Исправление ошибки производится по виду синдрома., так как каждому ошибочному разряду соответствует один-единственный проверочный вектор, Вид синдрома для каждой конкретной матрицы может быть определен при помощи: проверочной матрицы: Н, которая: представляет собой транспонированную матрицу П, дополненную единичной матрицей, число столбцов которой равно числу проверочных разрядов кода:, Столбцы такой матрицы представляют собой значение синдрома для разряда, соответствующего номеру столбца матрицы Н. Процедура исправления ошибок в процессе декодирования, групповых кодов сводится к следующему, Строится: кодовая: таблица. В первой строке таблицы: располагаются все кодовые векторы:, В первом столбце второй: строки размещается вектор, вес которого равен 1. Остальные позиции второй строки заполняются векторами, полученными в результате суммирования по модулю 2 вектора с вектором, расположенным: в соответствующем: столбце первой: строки. В первом столбце третьей: строки записывается: вектор, вес которого также равен 1, однако, если вектор содержит единицу в первом разряде, то - во втором. В остальные позиции: третьей строки: записывают суммы и. Аналогично поступают до тех пор, пока не будут просуммированы с векторами все векторы, весом 1, с единицами в каждом из п разрядов. Затем: суммируются по модулю 2 векторы, весом 2, с последовательным: перекрытием всех возможных разрядов. Вес вектора определяет число исправляемых ошибок. Число векторов, определяется возможным числом неповторяющихся синдромов и равно (нулевая комбинация говорит об отсутствии ошибки). Условие неповторяемости синдрома позволяет по его виду определять один-единственный соответствующий ему вектор, Векторы, есть векторы: ошибок, которые могу г быть исправлены данным групповым кодом, По виду синдрома принятая: комбинация может быть отнесена к тому или иному смежному классу, образованному сложением по модулю 2 кодовой комбинации с вектором ошибки, т, е. к определенной строке кодовой табл, 6.1, Таблица 6 Л
Принятая кодовая комбинация сравнивается с векторами, записанными в строке, соответствующей полученному в результате проверок синдрому. Истинный код будет расположен в первой строке той же колонки таблицы. Процесс исправления ошибки: заключается в замене на обратное значение разрядов, соответствующих единицам в векторе ошибок, Векторы не должны быть равны ни одному из векторов, в противном случае в таблице появились бы: нулевые векторы.
13.4 Тривиальные систематические коды. Код Хэмминга,
Систематические коды представляют собой такие коды, в которых информационные и: корректирующие разряды: расположены по строго определенной: системе и: всегда занимают строго определенные места, в кодовых комбинациях. Систематические коды: являются равномерными, т, е, все комбинации кода, с заданными корректирующими
способностями имеют одинаковую длину. Групповые коды: также являются систематическими, но не все систематические коды могут быть отнесены к групповым, Тривиальные систематические коды могут строиться, как и групповые, на основе производящей матрицы. Обычно производящая: матрица строится при помощи матриц единичной, ранг которой определяется числом информационных разрядов, и добавочной, 'число столбцов которой определяется числом контрольных разрядов кода, Каждая, строка добавочной матрицы должна содержать не менее единиц, а сумма, по модулю два любых строк не менее единиц (где - минимальное кодовое расстояние). Производящая матрица позволяет находить все остальные кодовые комбинации суммированием по модулю два строк производящей матрицы во всех возможных сочетаниях. Код Хэмминга является типичным примером систематического кода. Однако при: его построении: к матрицам: обычно не прибегают. Для вычисления основных параметров кода, задается либо количество информационных символов, либо количество информационных комбинаций. При помощи (59) и (60) вычисляются и. Соотношения между для кода..Хэмминга представлены в табл. 1 приложения 8. Зная основные параметры корректирующего кода, определяют, какие позиции сигналов будуг рабочими, а какие контрольными, Как показала, практика, номера контрольных символов удобно выбирать по закону, где и: т.д. - натуральный ряд чисел. Номера контрольных символов в этом случае будут соответственно: 1, 2.. 4, 8, 16, 32 и т, д. Затем определяют значения контрольных коэффициентов (0 или 1), руководствуясь следующим правилом: сумма единиц на контрольных позициях должна быть четной. Если эта сумма, четна, то значение контрольного коэффициента - 0, в противном случае - 1, Проверочные позиция: выбираются следующим: образом: составляется таблица для ряда натуральных чисел в двоичном коде. Число строк таблицы
Первой строке соответствует проверочный коэффициент, второй и т.д., как показано в табл, 2 приложения 8, Затем: выявляют проверочные позиции, выписывая: коэффициенты: по следующему принципу: в первую проверку входят коэффициенты, которые содержат в младшем разряде 1, т.е. и: т. д.: во вторую - коэффициенты, содержащие 1 во втором:
разряде, т.е. и т.д.; в третью проверку ™ коэффициенты, которые содержат 1 в третьем разряде, и т. д. Номера проверочных коэффициентов соответствуют номерам един, что позволяет составить общую таблицу проверок (табл. 3, 8). Старшинство разрядов считается слева направо, а при проверке сверху Порядок проверок показывает также порядок следования разрядов в полученном коде. Если в принятом коде есть ошибка, то результаты проверок по
та обратный:. Для: кроме проверок по следует проводить еще одну проверку на четность для каждого кода.. Чтобы осуществить такую проверку, следует к каждому коду в конце кодовой
| Лекция 14. Т«кодов. |
| средства кодирования и |
| одирования для групповых |

| поэтому |
полученной комбинации: всегда была четной. Тогда в случае одной ошибки проверки: по позициям укажут ном:ер ошибочной позиции, а проверка на четность укажет наличие ошибки. Если проверки: позиций укажутна наличие ошибки, а проверка на четность не фиксирует ошибки, значит в коде две ошибки
Относительная скорость кода RK показывает относительное число разрешенных кодовых комбинаций в коде и вычисляется по формуле:
Величина 1 - RK является коэффициентом избыточности кода.
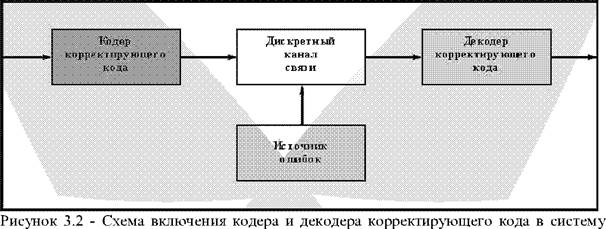
Схема включения кодера и декодера корректирующего кода в систему передачи дискретных сообщений двоичными кодами представлена на рисунке 3.2.
|
передачи дискретных сообщений двоичными кодами
На вход кодера поступает последовательность двоичных символов ai а2....а^, представляющих собой безызбыточные кодовые комбинации А;, соответствующие знакам сообщения. В процессе кодирования кодовые комбинации А; значности к преобразуются в п - разрядные кодовые комбинации В; с символами bi b2....bk bk+i....bn (n>k), т.е. кодер вводит в безызбыточные кодовые комбинации г = n - к проверочных символов.
Скорость такого кода можно вычислить с учетом, что Ма = 2к и Мп = 2": Rk = к/п.
Принятая кодовая комбинация В; (bi b2.....b„) может в любом символе отличаться от переданной в результате воздействия ошибок, возникающих на выходе дискретного канала связи, поэтому каждый из ее символов обозначается со штрихом.
В декодере при избыточном кодировании появляется возможность обнаружения и исправления этих ошибок, для реализации этой возможности все кодовые комбинации корректирующего кода разбиваются на разрешенные и запрещенные. На выходе кодера формируются и далее передаются по дискретному каналу только разрешенные Bip кодовые комбинации. Переход их в запрещенные под действием ошибок является необходимым условием для обнаружения и исправления ошибок.
Поэтому главная задача построения любого корректирующего кода - разбиение всех Мо кодовых комбинаций на Ма разрешенных и Mq - Ма запрещенных так, чтобы обеспечить заданную корректирующую способность кода.
Декодирование с обнаружением ошибок: методика проста - принятая кодовая комбинация поочередно сравнивается со всеми разрешенными, и если она не совпадает ни с одной из них, то выносится решение о наличии ошибок.
Для обнаружения ошибок кодовое расстояние между любыми двумя разрешенными кодовыми комбинациями должно быть достаточным для того, чтобы при изменении одного или нескольких символов в них под воздействием ошибок не возникла снова разрешенная кодовая комбинация, т.е. для обнаружения ошибок кратности glimiI кодовое расстояние dt1 должно быть хотя бы на единицу больше кратности обнаруживаемых ошибок gaffln, т.е.:
Исправление ошибок возможно только в случае, когда переданная разрешенная кодовая комбинация переходит в запрещенную. Это производится в декодере на основании сравнения принятой запрещенной комбинации со всеми разрешенными. Принятая кодовая комбинация отождествляется с той из разрешенных, на которую она больше похожа, т.е. с той, от которой она отличается меньшим числом элементов.
Согласно этому правилу: для исправления ошибок кратностью g и.ош необходимо, чтобы запрещенная кодовая комбинация, получаемая при g„.mij- кратных ошибках, оставалась ближе к истинной, чем к любой друтой разрешенной комбинации. Это выполняется при условии:
'^^'Йгаш!
Если соседние разрешенные кодовые комбинации находятся на кодовом расстоянии d„=5, то при ошибках кратности четыре и меньше любая разрешенная комбинация не может перейти в другую разрешенную и факт наличия ошибок не обнаруживается. Исправляться могут только одно- и двухкратные ошибки, так как уже при трех ошибках полученная запрещенная кодовая комбинация окажется ближе к друтой разрешенной.
На практике получили распространение такие методы кодирования и декодирования, которые имеют приемлемую сложность реализации. Одним из таких способов декодирования является синдромный способ, основанный на простом правиле: для исправления ошибки необходимо знать не только факт ее существования, но и местонахождение. Под синдромом кода понимают контрольное число, указывающее на наличие и расположение (конфигурации) ошибок в кодовой комбинации.
Не нашли, что искали? Воспользуйтесь поиском: