
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ТЕМА 3. ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХ.
Группировка - основной метод статистики.
Виды статистических группировок.
Принципы выбора группировочного признака. Образование групп и интервалов группировки.
Статистические ряды распределения.
Вопрос 1.
Группировка статистических данных является основой научной сводки и обработки данных. По своему содержанию статистическая сводка представляет собой совокупность приемов, позволяющих получить обобщенную характеристику изучаемого явления по ряду существенных для него признаков. Статистическая сводка включает следующие операции:
1. Группировку данных статистического наблюдения, т.е. составление рядов распределения
2. Суммирование (это сводка в узком понимании) показателей по отдельным группам и по всей совокупности, т.е. получение статистических показателей в абсолютной форме.
3. Расчет на основе абсолютный показателей статистических показателей в относительной форме.
4. Табличное или графическое оформление результатов сводки и их анализ.
Таким образом, первым этапом проведения статистической сводки является группировка статистических данных наблюдения, поэтому группировка является решающим звеном статистической сводки. Она позволяет выявить и отграничить разнокачественные единицы наблюдения, входящие в совокупность и одновременно объединить в группы одно-качественные единицы наблюдения.
Статистическая группировка представляет собой процесс образования однородных групп на основе расчленения статистической совокупности на части или объединение изучаемых единиц в частные совокупности по существенным для них признакам.
Признаки, по которым производится распределение единиц наблюдаемой совокупности на группы, называют группировочными признаками или основанием группировки (например, совокупность предприятий можно прогруппировать по следующим признакам - объем товарооборота, численность работников и т.д.).
Статистические группировки позволяют решить следующие задачи:
1. Выделить типы и существенно различные стороны, составляющие сложное общественное явление
2. Охарактеризовать выделенные типы и формы системой статистических показателей
3. Установить взаимосвязи между отдельными типическими группами
4. Определить характер взаимодействия между отдельными признаками совокупности в целом и по составляющим ее группам
3. Оценить влияние факторов на изменение результативного признака.
Вопрос 2.
Исходя из задач, решаемых с помощью статистических группировок, в теории статистики выделяют следующие виды группировок:
1. Типологические группировки. Содержанием является выделение из множества признаков, характеризующих изучаемое явление, основных типов в качественно однородные. Типологические группировки широко применяются в экономических, социальных и др. исследованиях. Необходимость проведения типологической группировки обусловлена потребностью теоретического обобщенная первичной статистической информации и получения на этой основе обобщающих статистических показателей. При использовании метода типологических группировок важное значение имеет правильный выбор группировочного признака.
2. Структурные группировки. Выделенные типы явлений с помощью типологической группировки могут изучаться с точки зрения их структуры и состава. При этом используются структурные группировки, т.е. группировки применяемые для изучения строения совокупности.
3. Аналитические группировки - наиболее распространенный вид. Они применяются для выявления взаимосвязи между двумя или несколькими признаками общественных явлений (например, группировка предприятий по численности рабочих).
Вопрос 3.
Важнейшим вопросом теории группировок является выбор группировочных признаков, т. к. от выбора группировочного признака зависят результаты группировки, которые получают в процессе ее разработки. Статистика выделяет следующие основные правила выбора группировочных признаков:
1) при выборе группировочных признаков необходимо руководствоваться знанием сущности данного явления, законов его развития;
2) в основание группировки должно быть положено необходимое число наиболее существенных признаков, отвечающих задачам исследования;
3) группировочные признаки должны отбираться с учетом конкретных особенностей изучаемых явлений;
4) для всесторонней характеристики сложных общественных явлений целесообразно брать несколько группировочных признаков (два или более).
Признаки, положенные в основу группировки, могут быть качественные (атрибутивные) или количественные (имеющие числовое выражение).
При проведении группировок важное значение имеют правильное решение о том, на какое число групп следует подразделять совокупность. Если признак атрибутивный, то число групп, на которое следует подразделять совокупность, определяется числом качественных градаций этого признака. В случае, если группировочный признак количественного порядка, непрерывный или дискретный, с большим размахом вариации, то число групп может быть определено:
1. расчетным путем по формуле Стерджесса:
n = 1+3,322 IgN,
где n - число групп, N - численность совокупности;
2. по нормативам, а именно:
если численность совокупности не превышает 25-30 единиц, то в расчет принимается 3-4 группы,
30-40 - 5-6 групп;
40-60 - 6-8 групп.
При определении числа группировок необходимо их выбор производить таким образом, чтобы каждая группа была представительной, т. е. содержала не менее 7-10 единиц наблюдения, причем центральная часть интервала должна содержать не менее 50%.
Для характеристики групп должны быть образованы интервалы, которые могут быть равные и неравные, открытые и закрытые. При равных интервалах их величина определяется по формуле:
h = (Xmax – Xmin) / n = R / n; где n - число групп, R - размах вариации.
При построении равных интервалов определяется нижняя и верхняя граница каждого из них, причем считается, что пределы наблюдения могут входить «включительно» или «исключительно». На практике применяются оба метода, но все же предпочтительнее принцип «исключительно».Например, группы работников магазина по производительности труда обозначены следующим образом: до 90 руб.; 90-120; 120-150; 150-180; свыше 180 руб. По принципу «включительно» к первой группе относится работник, производительность труда которого обозначается — до 90 руб.; по принципу «исключительно» этот работник включается во вторую группу—90—120 руб. Применение этих принципов зависит от формы написания интервалов, особенно первой и последней групп. В данном примере работника, производительность которого 180 руб., включают в предпоследнюю группу, поскольку ее интервал обозначен 150—180, а последний—свыше 180 руб. Соответственно работник, имеющий выработку 90 руб., Относится к первой группе. Если бы запись была «180 и более», то по принципу «исключительно» работник, имеющий выработку 180 руб., включался бы в последнюю группу.
Открытые интервалы не имеют для 1-го интервала нижней границы, а для последнего – верхней.
Неравные интервалы могут применяться при значительной вариации признака совокупности. Определяющим при этом является качественная однородность групп. Для характеристики установленных групп и их интервалов необходимо правильное определение показателей, которыми характеризуется каждая группа. При этом выбор показателей должен:
1) отразить общую картину развития экономического процесса;
2) проявить особенности каждого типа;
3) установить специфику проявления типа групп ли формы подгрупп применительно к различным регионам и зонам. Тщательный отбор показателей для анализа позволяет повысить результативность статистической группировки.
Серединное значение интервалов определяется:
Этот показатель можно рассчитать суммированием верхней и нижней границ интервала и делением суммы пополам. В нашем примере во втором интервале середина равна 105 руб. (90+120):2; в третьем - 135 руб.: (120+150): 2; в первом интервале - 75 руб. (60+90):2. Поскольку первый интервал является открытым (не имеет нижней границы), а имеющийся ряд распределения – интервальный, причем с равными интервалами (в 30 руб.), то предполагается, что нижней границей первого интервала будет является значение в 60руб. (90 – 30).
Вопрос 4.
Результаты сводки и группировки материалов статистического наблюдения оформляются в виде статистических рядов распределения и таблиц.
Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку. Они характеризуют состав (структуру) изучаемого явления, позволяют судить об однородности совокупности, границах ее изменения, закономерностях развития наблюдаемого объекта.
Ряды распределения, образованные по качественным признакам, называют атрибутивными. Например, распределение работников торговли по занимаемой должности, профессии, образованию; распределение товарооборота по формам торговли, товарным группам; распределение работников по возрасту, стажу работы, производительности труда, заработной плате и другим признакам. При группировке ряда по количественному признаку получаются вариационные ряды. При этом вариационные ряды по способу построения бывают дискретными (прерывными), основанными на прерывной вариации признака (например, число касс в магазине, комнат в квартире), и интервальными (непрерывными), базирующимися на непрерывно изменяющемся значении признака, имеющими любые (в том числе и дробные) количественные выражения (объем товарооборота, величина фонда оплаты труда, выработка продавца). В практике применяются также и интервальные ряды распределения. При их построении возникают вопросы о числе групп, величине интервала, его границе.
Вариационные ряды состоят из двух элементов: варианты и частоты. Варианта - это отдельное значение варьируемого признака, которое он принимает в ряду распределения. Частотами называются численности отдельных вариант или каждой группы вариационного ряда. Частоты, выраженные в долях единицы или в процентах к итогу, называются частостями. Сумма частот составляет объем ряда распределения.
Каждый ряд распределения может быть представлен графически. Графическое изображение рядов распределения облегчает их анализ и позволяет судить о форме распределения наглядно.
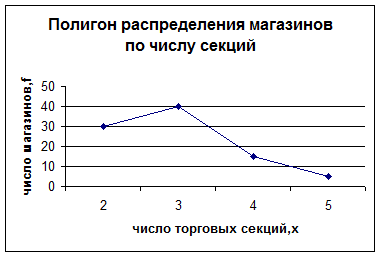
Для графического изображения дискретного ряда применяют полигон распределения. Для его построения на оси абсцисс откладывают значения признака, а на оси ординат - частоту.
Например, в таблице представлен ряд распределения магазинов по числу торговых секций
| Число секций (варианта - х) | Количество магазинов (частота – f) |
Данный ряд распределения является дискретным, так как варианта (число секций) представлена здесь целым числом (2,3,4,5), и полигон распределения данного ряда будет иметь следующий вид:
Для графического изображения интервального вариационного ряда применяется гистограмма. При ее построении на оси абсцисс откладываются интервалы ряда, высота которых равна частотам, отложенным на оси ординат. Над осью абсцисс строятся прямоугольники, площадь которых соответствует величинам произведений интервалов на их частоты.
| Группы магазинов по числу секций (варианта – х задана в виде интервала) | Количество магазинов (частота – f) |
| 2-4 4-6 6-8 |
Графическое изображение (гистограмма) данного ряда распределения будет иметь следующий вид:
Число магазинов, f



 40 -
40 -
 20 -
20 -



2 4 6 8 группы магазинов по числу секций, х
В практике экономической работы возникает потребность в преобра- зовании рядов распределения в кумулятивные ряды, строящиеся по накопленным частотам. (с их помощью можно определить структурные средние, прослеживать за процессом концентрации изучаемого явления). Используя накопленные частоты строят график в виде кумуляты (кривой сумм). При графическом изображении кумуляты накопленные частоты наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Длина этих линий равна величине накопленных частот в конкретном интервале. Соединяя затем эти перпендикуляры, получаем ломаную линию.
| Группы магазинов по числу секций (варианта – х заданная в виде неравных интервалов) | Количество магазинов (частота – f) | Накопленная частота - 
|
| 2-4 4-6 6-8 | 55 (20+35) 70 (15+55) |
Графическое изображение (кумулята) данного ряда распределения, построенного по накопленным частотам, будет иметь следующий вид:
накопленная частота, f ‘

100 -



 -
-
 50
50

2 4 6 8 х, группы магазинов по числу секций
Не нашли, что искали? Воспользуйтесь поиском: