
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ
ДИСКРЕТНЫЕ МОДЕЛИ
Дискретной моделью уравнений
 , (1)
, (1)
 (2)
(2)
называется [1, 2, 3, 4, 5] система разностных уравнений
 , (3)
, (3)
 , (4)
, (4)
реакция которых  совпадает в точках
совпадает в точках  с решениями системы (1), (2),
с решениями системы (1), (2),  .
.
 -
-  -мерный вектор состояний,
-мерный вектор состояний,  -
-  -мерный вектор выходных переменных,
-мерный вектор выходных переменных,  -
-  -мерный вектор входных переменных (управлений);
-мерный вектор входных переменных (управлений);  ,
, 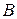 ,
,  ,
,  ,
,  ,
,  - матрицы чисел соответствующих размеров. Матрицы
- матрицы чисел соответствующих размеров. Матрицы  и
и  связаны с матрицами
связаны с матрицами  и
и 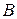 следующими соотношениями
следующими соотношениями
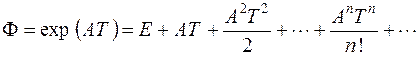 , (5)
, (5)
 . (6)
. (6)
В случае, если  - неособенная матрица (
- неособенная матрица ( ), то
), то  можно определить следующим образом
можно определить следующим образом
 . (7)
. (7)
Пример 1. Рассмотрим упрощенную модель задачи управления самолетом по углу курса в горизонтальном полете. Предположим, что порывы ветра разворачивают самолет относительно требуемого направления и нужно корректировать ошибки курса с помощью отклонений руля. Будем рассматривать только плоское движение, считая самолет твердым телом в виде отрезка прямой и полагая угловые отклонения малыми.

1 - осевая линия самолета,
2 - расчетное направление полета,
3 - ось курса,
4 - руль.
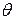 - ошибка курса;
- ошибка курса;  - отклонение руля;
- отклонение руля;  - момент инерции самолета относительно оси, перпендикулярной плоскости чертежа (то есть при его вращении по
- момент инерции самолета относительно оси, перпендикулярной плоскости чертежа (то есть при его вращении по 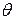 ).. Восстанавливающий момент считаем пропорциональным отклонению руля (вязким сопротивлением вращению со стороны воздуха и связью между углами курса и крена пренебрегаем).
).. Восстанавливающий момент считаем пропорциональным отклонению руля (вязким сопротивлением вращению со стороны воздуха и связью между углами курса и крена пренебрегаем).
Решение.
В силу второго закона Ньютона
 ,
,
где  - коэффициент пропорциональности между отклонением руля и восстанавливающим моментом (
- коэффициент пропорциональности между отклонением руля и восстанавливающим моментом ( );
);  - момент, вызываемый порывом ветра (возмущающий момент).
- момент, вызываемый порывом ветра (возмущающий момент).
Разделим на  и введем обозначения
и введем обозначения
 ,
,  ,
,  ,
,
тогда
 .
.
Полученное дифференциальное уравнение имеет второй порядок. Поэтому для его решения кроме знания 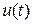 ,
,  , требуется задать два начальных условия:
, требуется задать два начальных условия:
 - начальная ошибка по углу курса;
- начальная ошибка по углу курса;
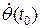 - начальная ошибка по скорости изменения угла курса.
- начальная ошибка по скорости изменения угла курса.
Вводя переменные
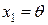 ,
,  ,
,
получим
 ,
,
или
 .
.
 - вектор состояния, состоящий из двух физических величин: ошибки по углу курса и ошибки по скорости изменения угла курса.
- вектор состояния, состоящий из двух физических величин: ошибки по углу курса и ошибки по скорости изменения угла курса.
Уравнения можно записать в виде (1)
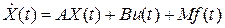 ,
,
где
 ,
, 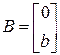 ,
,  .
.
Приведем данные уравнения к дискретному виду.
 .
.
Так как  ,
,  ,..., то
,..., то  .
.
Следовательно,
 .
.
Аналогично
 ,
,
или
 .
.
Матрица  определяется аналогично
определяется аналогично  (
( - матрица при возмущениях в дискретной модели).
- матрица при возмущениях в дискретной модели).
 .
.
Таким образом, система описывается следующей дискретной моделью:
 или
или
 .
.
Пример 2. Математическая модель линейной стационарной динамической системы в непрерывном случае имеет вид
 .
.
Записать дискретную модель системы.
Решение.
 ,
,
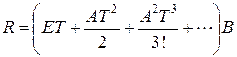 .
.
Так как
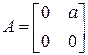 ,
, 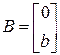 ,
,
то
 .
.
Поэтому
 ,
,
 .
.
Дискретная модель принимает вид
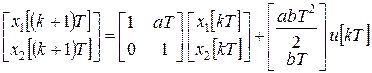
или
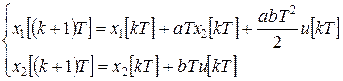 .
.
Пример 3 [2, с.246]. Математическая модель линейной стационарной системы в непрерывном случае имеет вид
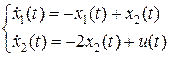 .
.
Записать дискретный вид математической модели.
Решение.
Легко показать, что
 .
.
Тогда
 ,
,
 .
.
Поэтому дискретная модель имеет вид:
 .
.
Пример 4 [4, с.127]. Математическая модель линейной стационарной системы в непрерывном случае имеет вид
 ;
;
 ,
,
где  ,
, 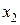 - переменные состояния;
- переменные состояния;  ,
, 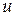 - скалярные выходная и входная переменные соответственно. Записать дискретный вид математической модели системы для
- скалярные выходная и входная переменные соответственно. Записать дискретный вид математической модели системы для  с.
с.
Решение.
Можно показать, что
 .
.
В силу этого
 ,
,
 .
.
Следовательно, дискретная математическая модель имеет вид

 .
.
Положим период дискретности  с, тогда
с, тогда
 ,
,
или
 .
.
2. АНАЛИЗ ДИСКРЕТНЫХ СТАЦИОНАРНЫХ СИСТЕМ
Для дискретных систем роль дифференциальных уравнений в переменных состояния играют разностные уравнения
 ,
,  . (8)
. (8)
Решение уравнений (8) может быть получено следующим образом. Придавая индексу  значения
значения  ,
,  ,
,  ,
,  ,
,  , запишем:
, запишем:

 ;
;

 =
= 
 =
=  =
=
 ;
;

 =
= 

 .
.
В общем случае, при произвольном  , имеем
, имеем
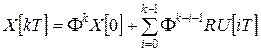 . (9)
. (9)
Это общее решение первого уравнения (8).
Первое слагаемое (9) зависит только от начальных условий и определяет реакцию системы, не зависящую от входного (управляющего) воздействия  . Это слагаемое называется свободной составляющей
. Это слагаемое называется свободной составляющей
 . (10)
. (10)
Второе слагаемое (9) зависит только от значений  ,
,  ,...,
,...,  и называется вынужденной составляющей
и называется вынужденной составляющей
 . (11)
. (11)
Замечание. Матрица  называется переходной матрицей состояния дискретной системы или фундаментальной матрицей.
называется переходной матрицей состояния дискретной системы или фундаментальной матрицей.
Пример 5 [5, с.201]. Определить взвешенную временную последовательность  .
.
По определению  - реакция системы при нулевых начальных условиях
- реакция системы при нулевых начальных условиях  и входе в виде дельта последовательности
и входе в виде дельта последовательности
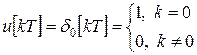 .
.
 называется дельта-последовательностью Кронеккера.
называется дельта-последовательностью Кронеккера.
Решение.
В данном случае из выражения (8) при  ,
,  ,
,  ,
,  имеем
имеем

 ,
,  ;
;

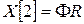 ,
,  ;
;

 ,
,  .
.
При произвольном  получим
получим
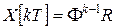 ,
,  .
.
Итак, искомая взвешенная временная последовательность определяется формулой
 . (12)
. (12)
Пример 6 [3, c.202]. Задана математическая модель дискретной системы
 ;
;
 .
.
Определить реакцию системы на входное воздействие в виде дельта-последовательности Кронеккера, то есть взвешенную временную последовательность  .
.
Воспользуемся выражением (12), в котором полагаем
 ,
,  ,
,  .
.
Тогда (12):
 ,
,  .
.
Для вычисления

применим формулу Сильвестра (Лагранжа-Сильвестра). Собственные значения матрицы определяются характеристическим уравнением
 , откуда
, откуда  ,
,  .
.
Получаем
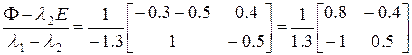 ;
;
 .
.
Подставляя в формулу (12)  , найдем
, найдем

 =
= 


Пример 7. Математическая модель линейной стационарной динамической системы в непрерывном случае имеет вид
 (13)
(13)
Записать дискретный вид математической модели системы для  с и построить графики изменения
с и построить графики изменения  ,
,  ,
,  ,
,  на интервале времени
на интервале времени  . Начальные условия
. Начальные условия 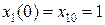 ,
,  ; входное воздействие:
; входное воздействие:  - для дискретной модели;
- для дискретной модели;  - для непрерывной модели.
- для непрерывной модели.
Решение
Дискретная модель системы получена в примере 4 и имеет вид
 . (14)
. (14)
Решение уравнений (13) можно получить по формуле Коши
 . (15)
. (15)
Подставляя в (15)  ,
,  ,
,  ,
,  ,
,  , получаем значения
, получаем значения  ,
,  , которые сводим в табл. 1.
, которые сводим в табл. 1.
Таблица 1
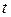
| ||||||

| 0.8002 | 0.6262 | 0.5485 | 0.5181 | 0.5067 | |

| -0.2325 | -0.1170 | -0.04731 | -0.018 | -0.00669 | |
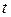
| ||||||

| 0.5025 | 0.5010 | 0.5003 | 0.5001 | 0.5 | |

| -0.0025 | -0.0009 | -0.000335 | -0.123×10-3 | -0.45×10-3 |
Для построения дискретного процесса полагаем в (14)  ,
,  ,
,  ,
,  ,
,  . Получаем значения
. Получаем значения  ,
,  , которые сводим в табл. 2.
, которые сводим в табл. 2.
Таблица 2

| ||||||

| 0.8 | 0.6257 | 0.5481 | 0.5179 | 0.507 | |

| -0.233 | -0.1172 | -0.0472 | -0.0178 | -0.007 | |

| ||||||

| 0.502 | 0.5009 | 0.5003 | 0.5001 | 0.5 | |

| -0.002 | -0.88×10-3 | -0.32×10-3 | -0.0001 | -0.0004 |
Примечание. Полученные расхождения между  ,
,  и
и  ,
,  в точках
в точках  ,
,  ,
,  ,
,  ,
,  оси времени объясняются погрешностями вычисления
оси времени объясняются погрешностями вычисления  ,
,  и
и  ,
, 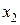 .
.
Строим графики:




Пример 8. Ссуда под недвижимость в сумме 50 тысяч долларов должна быть возвращена через 30 лет равными ежемесячными взносами размером p долларов. Выплачиваемый процент установлен 15% в год от невозвращенной (оставшейся) суммы.
Определим модель процесса.
Пусть x[kT] –неоплаченная часть ссуды, оставшейся после выплаты k -го ежемесячного взноса. Тогда
 (16)
(16)
где  - ежемесячная норма процента. Таким образом, модель – разностное уравнение первого порядка.
- ежемесячная норма процента. Таким образом, модель – разностное уравнение первого порядка.
Зная модель, можно исследовать процесс. Например, поставить следующие задачи:
· определить Р (сколько нужно выплачивать ежемесячно);
· определить общую сумму выплат за 30 лет.
Решим эти задачи.
Полагаем в (3) 
Тогда (9) принимает вид
 . (17)
. (17)
Откуда
 . (18)
. (18)
 (19)
(19)
Воспользуемся формулой для частичной суммы геометрической прогрессии
 (20)
(20)
Полагаем в (20)  и m=k-1, получим из (19)
и m=k-1, получим из (19)
 (21)
(21)
Подставим (21) в (18)
 (22)
(22)
Окончательно сумма взноса P, которую требуется выплачивать ежемесячно в течение 30 лет (360 месяцев)
|
 . (23)
. (23)
При r=0,0125 (15% в год) и x[0]=50000, находим P=632,22 доллара.
Полная сумма возврата в банк за ссуду в 50000 долларов составляет 360 p=227599,2 доллара, которая убедительно иллюстрирует, почему банки охотно дают займы.
ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ
Задана непрерывная модель линейной стационарной системы (табл. 3).
1. Построить дискретную математическую модель системы. Период дискретности  задается преподавателем.
задается преподавателем.
2. Определить взвешенную временную последовательность.
3. Построить графики изменения  ,
,  ,
,  ,
,  на заданном преподавателем отрезке времени.
на заданном преподавателем отрезке времени.
 или
или  .
.
Таблица 3
| Вариант | Математическая модель системы | 
| ||||

| 
| |||||

| 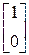
| |||||

| 
| |||||

| 
| |||||

| 
| |||||

| 
| |||||

| 
| |||||

| 
| |||||

| 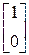
| |||||

| 
| |||||

| 
| |||||

| 
| |||||

| 
| |||||
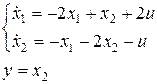
| 
| |||||

| 
| |||||

| 
| |||||

| 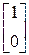
| |||||

| 
| |||||

| 
| |||||
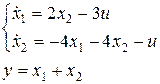
| 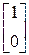
| |||||

| 
| |||||
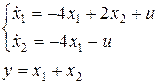
| 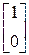
| |||||
ЛИТЕРАТУРА
Основная
1. Деруссо П., Рой Р., Клоуз Ч. Пространство состояний в теории управления. - М.: Наука,1970.
2. Директор Р., Рорер С. Введение в теорию систем. - М.: Высшая школа, 1971.
3. Иванов В.А., Ющенко А.С. Теория дискретных систем автоматического управления. - М.: Наука, 1983.
4. Куо Б. Теория и проектирование цифровых систем управления. - М.: Машиностроение, 1986.
5. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. - М.: Машиностроение, 1985.
Дополнительная
6. Автоматизированное проектирование систем автоматического управления /Под ред. В.В. Солодовникова. - М.: Машиностроение, 1990.
7. Сигорский В.П. Математический аппарат инженера. - Киев: Техника, 1977.
8. Ту Ю. Современная теория управления. - М.: Машиностроение, 1971.
ОСНОВЫ АНАЛИТИЧЕСКОГО АНАЛИЗА
ЛИНЕЙНЫХ МНОГОМЕРНЫХ ДИСКРЕТНЫХ СИСТЕМ
Методические указания и контрольные задания
по дисциплине "Основы аналитической теории анализа и синтеза САУ"
для студентов специальности 210100 и направления 550200
Составили: ЛЬВОВ АЛЕКСЕЙ АРЛЕНОВИЧ
ТИМОФЕЕВ ЮРИЙ КОНСТАНТИНОВИЧ
Рецензент С.А. Моисеенко
Редектор Р.А. Козина
| <== предыдущая лекция | | | следующая лекция ==> |
| egrave; ФГД 2, 50% ФГД 3-4 | | | R Первая тормозная позиция |
Не нашли, что искали? Воспользуйтесь поиском:
