СЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ЛИС-ЦЕПИ

Задача 4.1. Стационарная случайная последовательность генерируется в соответствии с выражением
,

где 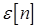– белый шум с нулевым математическим ожиданием и дисперсией . Найдите следующие вероятностные характеристики последовательности : математическое ожидание 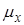, дисперсию 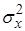, корреляционную последовательность , спектральную плотность мощности .

Задача 4.2. Оптимальный одношаговый линейный предсказатель для последовательности , определенной в предыдущей задаче, описывается уравнением 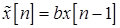. Найдите параметр 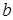и дисперсию ошибки предсказания оптимального предсказателя. Найдите спектральную плотность мощности ошибки предсказания. Как будет изменяться ошибка предсказания при увеличении порядка линейного предсказателя?

Задача 4.3. Цифровая цепь описывается разностным уравнением 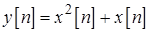. Как изменится математическое ожидание стационарного случайного процесса при прохождении через эту цепь?

Задача 4.4. Цифровая цепь описывается разностным уравнением . Найдите автокорреляционную функцию случайной последовательности на выходе цепи, при условии, что на ее вход воздействует стационарный белый шум.

Задача 4.5. Цифровая цепь описывается разностным уравнением 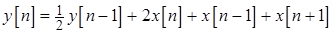. Найдите автокорреляционную функцию случайной последовательности на выходе цепи, при условии, что на ее вход воздействует стационарный белый шум.

Задача 4.6. Цифровая цепь описывается разностным уравнением 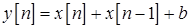. Найдите математическое ожидание, дисперсию и корреляционную функцию случайной последовательности на выходе цепи при условии, что на ее вход воздействует последовательность независимых случайных величин с нулевым математическим ожиданием и дисперсией .

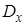Задача 4.7. Может ли для оценивания текущей дисперсии стационарной случайной последовательности с нулевым средним использоваться выражение .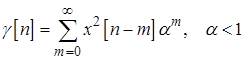

Если да, то как?

Задача 4.8. Сигнал, передаваемый по каналу связи, подвергается воздействию помехи в соответствии с моделью

,

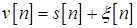где 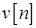– наблюдаемая последовательность, 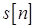– полезный сигнал (стационарная в широком смысле случайная последовательность с нулевым средним и известной АКП), – стационарный белый шум с нулевым средним. Для подавления шума используется цифровой трансверсальный фильтр первого порядка, процесс на выходе которого обозначен 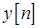. Определите параметры фильтра так, чтобы обеспечить минимум среднего квадрата ошибки между передаваемым 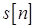и принимаемым 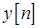сигналами.

Задача 4.9. Найдите математическое ожидание, дисперсию и корреляционную функцию случайной последовательности, определенной выражением

,

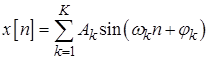где – независимые случайные величины, распределенные равномерно в интервале .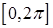

Задача 4.10. Найдите математическое ожидание, дисперсию и корреляционную функцию случайной последовательности, определенной выражением

,

где 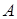, 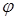– независимые случайные величины, 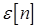– белый шум с нулевым математическим ожиданием и дисперсией . Случайная величина 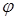распределена равномерно в интервале .

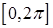Задача 4.11. Найдите математическое ожидание, дисперсию и корреляционную функцию случайной последовательности, определенной выражением

,

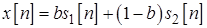где 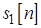, – некоррелированные стационарные случайные последовательности с известными АКП, 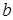– дискретная случайная величина, принимающая значение с вероятностью 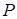и значение 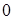– с вероятностью .

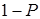Задача 4.12. Дана случайная последовательность , описываемая следующим некаузальным разностным уравнением

,

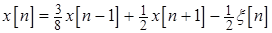где – последовательность независимых гауссовских случайных величин с нулевым математическим ожиданием и единичной дисперсией. Найдите эквивалентное каузальное представление последовательности .

Задача 4.13. Выполните методом минимизации ошибки линейного предсказания приближенную спектральную факторизацию случайной последовательности имеющей корреляционную функцию

.

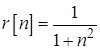Для аппроксимации заданной характеристики используйте линейный предсказатель первого порядка. Найдите корреляционную последовательность приближенного представления и сравните ее с исходной последовательностью.

Задача 4.14. Выполните методом минимизации ошибки линейного предсказания приближенную спектральную факторизацию случайной последовательности, определяемой выражением

,

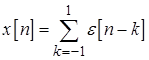где 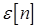– белый шум с дисперсией . Для аппроксимации используйте линейный предсказатель первого порядка. Найдите корреляционную последовательность приближенного представления и сравните ее с исходной последовательностью.

Не нашли, что искали? Воспользуйтесь поиском: