Спектральное представление случайных сигналов

В п.3.1 была показана эффективность представления детерминированных сигналов совокупностью элементар­ных базисных сигналов для облегчения анализа про­хождения их через линейные системы. Аналогичный подход может быть использован и в случае сигналов, описываемых случайными процессами.

Рассмотрим случайный процесс U(t), имеющий мате­матическое ожидание . Соответствующий центриро­ванный случайный процесс 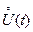характеризуется в любой момент времени 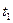центрированной случайной величиной :

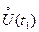. (3.49)

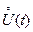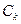Центрированный случайный процесс можно, как и ранее [см. (3.1)], выразить в виде конечной или бесконечной суммы ортогональных составляющих, каж­дая из которых представляет собой неслучайную базис­ную функцию с коэффициентом , являющимся случайной величиной. В результате имеем разложение центрированного случайного процесса :

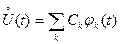(3.50)

Случайные величины 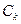называются коэффициентами разложения. В общем случае они статистически зави­симы и эта связь задается матрицей коэффициентов корреляции . Математические ожидания коэффи­циентов разложения равны нулю. Неслучайные базисные функции принято называть координатными функциями.

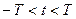Предположив, что , детерминированную функцию в (3.49) на интервале также можно разложить по функциям , представив в виде

, (3.50 а)

(3.50 б)

Подставляя (3.50 а) и (3.50 б) в (3.49) для случайно­го процесса U(t) с отличным от нуля средним, получим

(3.50 в)

Выражение случайного процесса в виде (3.50 в) позволяет существенно упростить его линейные преобра­зования, поскольку они сводятся к преобразованиям детерминированных функций , а коэффи­циенты разложения, являющиеся случайными величина­ми, остаются неизменными.

Чтобы определить требования к координатным функ­циям, рассмотрим корреляционную функцию процесса 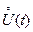, заданную разложением

.

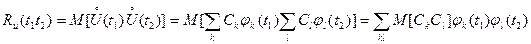Так как

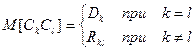
то

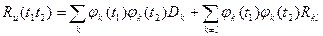(3.51)

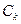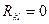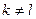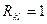Соотношение (3.51) становится значительно проще, если коэффициенты { } некоррелированы ( при , при ):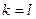

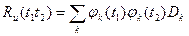(3.52)

В частности, при 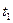= = 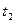t получим дисперсию случайного процесса U{t):

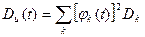(3.53)

Поэтому целесообразно выбирать такие координатные функции, которые обеспечивают некоррелированность случайных величин { 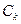}. Разложение (3.50), удовлет­воряющее этому условию, называют каноническим раз­ложением.

По известному каноническому разложению корреляционной функции случайного про­цесса можно записать каноническое разложение самого случайного процесса с теми же координатными функция­ми, причем дисперсии коэффициентов этого разложения будут равны дисперсиям коэффициентов разложения кор­реляционной функции.

Таким образом, при выбранном наборе координатных функций центрированный случайный процесс характери­зуется совокупностью дисперсий коэффициентов разло­жения, которую можно рассматривать как обобщенный спектр случайного процесса.

В каноническом разложении (3.50) этот спектр явля­ется дискретным (линейчатым) и может содержать как конечное, так и бесконечное число членов (линий).

Основным препятствием к широкому практическому использованию канонических разложений случайных процессов является сложность процедуры нахождения координатных функций. Однако для ряда стационарных случайных процессов эта процедура вполне приемлема.

Не нашли, что искали? Воспользуйтесь поиском: