ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Виды степенных средних и их свойства
| Вид степенной средней величины | Форма степенной средней величины | Описание | Формула для расчета | Пример | ||||
| Средняя арифметическая | простая (невзвешенная) | используется когда расчет осуществляется по несгруппированным данным. |  = (Х1+Х2+…+Хn): n = (Х1+Х2+…+Хn): n 
| Дано: Товарооборот (Хi) пяти торговый центров следующий (Х1, Х2, Х3, Х4, Х5): 130, 142, 125, 164 и 127 млн. руб. Рассчитаем среднюю арифметическую простую: (130+142+125+164+127): 5 = 136,7 млн.руб. | ||||
| взвешенная | используется когда отдельные значения осредняемого признака повторяются несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам (дискретным или интервальным). При расчете средней по интервальному вариационному ряду необходимые вычисления осуществляют по середине интервального ряда | 
| Дискретный ряд: рассчитать средний курс акций какого-то акционерного общества на торгах фондовой биржи. Известно, что сделки осуществлялись в течение 5 дней (5 сделок), количество проданных акций по курсу продаж распределилось следующим образом: 1день - 800 ак. по 1010 руб.; 2день - 650 ак. по 990 руб.; 3день -700 ак. по 1015 руб.; 4 день - 550 ак. по 900 руб.; 5 день - 850 ак. по 1150 руб.
Исходным соотношением для определения среднего курса стоимости акций является отношение общей суммы сделок (ОСС) к количеству проданных акций (КПА): ОСС = 1010×800 + 990×650+1015×700+900 × 550+1150×850 = 3634500; КПА = 800+650+700+550+ 850 = 3550. В этом случае средний курс стоимости акций был равен

| |||||
| Интервальный ряд:Определить среднюю прибыль организаций отрасли. | ||||||||
| Прибыль, млн. руб. | Середина интервала | Число фирм | ||||||
| до 20 20-30 30-40 40-60 60-80 80 и более | ||||||||
| Итого | - | |||||||
| Расчет средней арифметической взвешенной: (15×7+25×13+35×38+50×42+70×16+90×5): 121= 44,9 млн. руб. | ||||||||
| Средняя гармоническая | взвешенная | используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель, т.е. известны индивидуальные значения признака Х и произведение Х×f, а частоты f – неизвестны. | 
| Области ЦЧЭР | Валовой сбор, тыс. т | Урожайность, ц/га | ||
| Белгородская Воронежская Курская Липецкая Тамбовская | 0,5 | 16,1 9,5 4,8 10,9 7,0 | ||||||
Средняя урожайность могла бы быть рассчитана: Валовой сбор /Общая посевная площадь. Но показатель знаменателя (посевная площадь) неизвестен. Тогда используем формулу средней гармонической взвешенной, переведя тонны в центнеры
  = 9,9 ц/га = 9,9 ц/га
| ||||||||
| простая (невзвешенная) | Применяется в тех случаях, когда вес каждого варианта Х×f =1, то есть индивидуальные значения X встречаются по 1 разу |
 
| Вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической простой, мы вычисляем среднюю скорость:

| |||||
| Средняя геометрическая | простая (невзвешенная) | Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000) |
 = =  где Х1 , Х2, Х3…- цепные темпы роста
где Х1 , Х2, Х3…- цепные темпы роста
| Количество зарегистрированных преступлений за 4 года возросло в 1,57 раза, в т. ч. за 1-й – в 1,08 раза, за 2-й – в 1,1 раза, за 3-й – в 1,18 и за 4-й – в 1,12 раза. Тогда среднегодовой темп роста количества преступлений составляет:  , т.е. число зарегистрированных преступлений ежегодно росло в среднем на 12%. , т.е. число зарегистрированных преступлений ежегодно росло в среднем на 12%.
| ||||
| взвешенная | используется, когда временные интервалы неодинаковы | 
| ||||||
| Средняя квадратическая | простая (невзвешенная) | Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:
 Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.
Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.
| 
| |||||
| взвешенная | 
| |||||||
| В статистике могут применяться также степенные средние 3-го и более высоких порядков. | ||||||||
Б. Структурные средние: мода, медиана.
Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей.
Определение моды:
1) по несгруппированным данным.
Девять торговых фирм реализуют товар А по следующим ценам (тыс. руб.): 4,4; 4,3; 4,4; 4,5; 4,3; 4,3; 4,6; 4,2; 4,6. Наиболее часто встречается цена 4,3 тыс. руб. – она и является модальной (модой).
2) по сгруппированным данным:
- по дискретным рядам:
 Представим распределение торговых организаций города по уровню розничных цена на товар А. Представим распределение торговых организаций города по уровню розничных цена на товар А.
И таблицы видно, что наиболее распространенной является цена 55 руб., т.к. она наиболее часто встречается (в 60 организациях), поэтому цена 55 руб. является модальной (модой). - по интервальным рядам мода определяется по формуле:
где Мо – мода, x0 – значение начала модального интервала, h – размер модального интервала, fМо – частота модального интервала, fМо-1 – частота интервала, находящего перед модальным, fМо1 – частота интервала, находящего после модального.
Пример:
среднедушевых денежных доходов в 1998 г.
Интервал 400-600 в данном распределении будет модальным, т.к. имеет наибольшую частоту. Далее по формуле рассчитываем моду:
| Медиана – это значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Основное свойство медианы: сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Определение медианы: 1) по несгруппированным данным. Для начала выстоим ранжированный ряд: 4,2; 4,3; 4,3; 4,3; 4,4; 4,4; 4,5; 4,6; 4,6. Центральной в ряду является цена 4,4 тыс. руб. Причем, если ранжированный ряд имеет четное число единиц, то медиана определяется как средняя из двух центральных значений. 2) по сгруппированным данным: - по дискретным рядам: Сначала находим номер медианной единицы ряда по формуле:
В нашем случае Nme = (190 - 1): 2 = 95,5. Это означает, что точная середина находится между 95-ой и 96-ой организацией. Чтобы определить группу, к которой относятся организации с этими порядковыми номерами. Рассчитаем накопленные частоты 12+48=40; 12+48+56 =116. А значит организации с порядковыми номерами 95 и 96 относятся к группе организаций продающих товар А по цене 54 руб. – это цена и есть медиана. - по интервальным рядам медиана определяется по формуле:
где xMe — нижняя граница медианного интервала; iMe — ширина медианного интервала; ∑f/2 — количество всех значений, деленное на 2 (два); S(Me-1) — накопленная частота интервала, предшествующая медианному; fMe — частота медианного интервала.
Пример: Для определения медианного интервала рассчитываем накопленную частоту каждого последующего интервала до тех пор пока она не превысит ½ суммы накопленных частот (в нашем случае 73,35 = 146,7: 2): 22,1+27,8=49,9; 22,1+27,8+25,2 = 75,1. А значит, интеравал 600-800 является медианным.
Рассчитываем медиану по формуле:
|
Занятие № 15
Не нашли, что искали? Воспользуйтесь поиском:
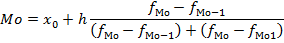
 Распределение населения РФ по уровню
Распределение населения РФ по уровню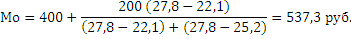
 где n – объем совокупности
где n – объем совокупности