
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Тема 5 Дифференциал функции
Студенту нужно разобраться с определением дифференциала функции и четко уяснить, что дифференциал функции (1,с.244) – главная линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной.
dy=f¢(x)Dx
Необходимо уяснить геометрический смысл дифференциала (1, с.245).
Дифференциал функции – есть приращение ординаты касательной, проведенной к графику функции y=f(x) в данной точке, когда х – получает приращение Dх.
Операция нахождения дифференциала сводится к нахождению производной и также называется дифференцированием функции.
Студенту необходимо уяснить сущность инвариантности формы дифференциала. Для этого нужно понять, что dy=f¢(x)dx и dy=f¢(u)du (1, с.246), если y=f(u), а u=j(x). Тогда по правилу дифференцирования сложной функции y¢=f¢(u)u¢, а u¢dx=du(1, с.244, формула 9.2) и dу=f¢(x)dx=f¢(u)u¢dx=f¢(u)du.
Вид формы (инвариантность формы – это независимость формы от дифференцируемой функции) дифференциала не меняется от характера дифференцируемой функции.
Весьма важным является практическое приложение дифференциала для приближенных вычислений. Необходимо уяснить из геометрического смысла дифференциала, что чем «круче» график функции, тем меньше нужно брать приращение аргумента Dх для вычисления функции с заданной точностью.
Необходимо разобрать задачи N9.1–9.3, 9.5–9.12 (1, с. 244–250) и аналогичные задачи по практикуму (2). При этом нужно понять, что последующее значение функции (1, с.247, пример 9.3) можно вычислять через предыдущее. Если предыдущее значение f(x)=  , а последующее f(x+Dx)=
, а последующее f(x+Dx)=  , то
, то  »
»  +
+ 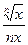 × Dx.
× Dx. 
Это так, ибо Dy=  –
– 

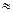
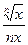 =f¢(x). Поэтому цепочка вычислений такова. Вычисляется предыдущее значение функции, а затем последующее. Чем меньше шаг по приращению аргумента х, тем больше точность вычисления функции.
=f¢(x). Поэтому цепочка вычислений такова. Вычисляется предыдущее значение функции, а затем последующее. Чем меньше шаг по приращению аргумента х, тем больше точность вычисления функции.
На вычислении дифференциала основаны многие численные методы в математике.
Студенту необходимо разобраться в вычислении относительной погрешности через дифференциал (1, с.247, 248) и эластичность функции (1, с.196) Ex(y)=x(y¢)/y.
Не нашли, что искали? Воспользуйтесь поиском: