
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Центры тяжести площадей простых геометрических фигур.
Задание №2
для расчетно-графической работы
«определение координат центра тяжести плоских сечений»
(примеры расчета)
Преподаватель: Фофанова В.В.
К выполнению задания рекомендуется приступить после изучения тем:
· Центр тяжести твердого тела;
· Центры тяжести площадей простых геометрических фигур, профилей проката.

Пример 1. Определить координаты центра тяжести сложного сечения. Показать положение центра тяжести на сечении.
1). Вычерчиваем сложное сечение в масштабе.
2). Делим сечение на простые геометрические фигуры и указываем их центры тяжести:
1 – прямоугольник 70х55 – т.С1
2 – треугольник (вырез) – т.С2
3 – полукруг – т.С3 (вырез)
3). Выбираем оси координат. (см.рис.)
4). Определяем координаты центров тяжести и площади простых фигур.
т. С1:
х1 = 
y1= 
А1 = 70*55 = 3850(мм2) 
т.С2:
х2 = 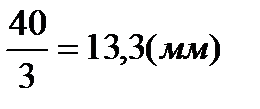
y1= 55 - 
А2 =  (мм2)
(мм2)
т.С3:
х3 = 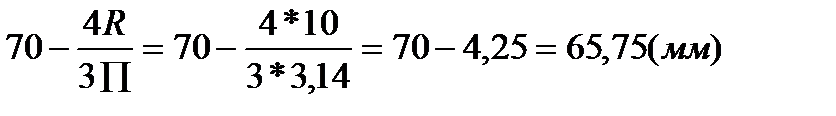
y3= 20(мм)
А3 = 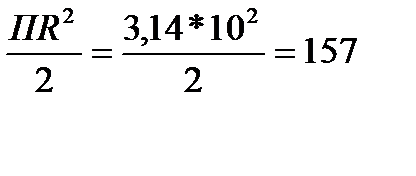 (мм2)
(мм2)
5). Определяем координаты ц.т сложного сечения:

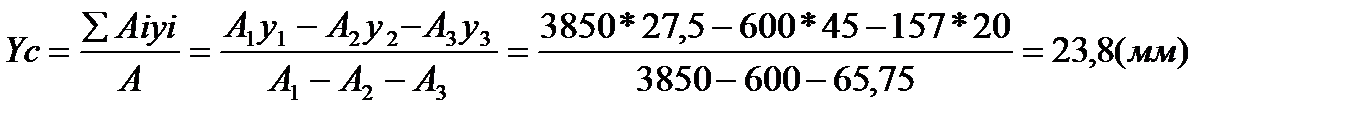
(Площади вырезов А2 и А3 – вычитаем)
6). Т.С(36,6мм; 23,8мм) – показываем на сечении.
Пример 2. Определить координаты центра тяжести сложного сечения. Показать положение центра тяжести на сечении.

1). Вычерчиваем сечение в масштабе. Делим сложное сечение на простые фигуры, указываем их центры тяжести.
1 – прямоугольник 80х30 – т.С1
2 – прямоугольник 50х40 – т.С2
3,4 – прямоугольные треугольники – т.С3, С4 (вырезы)
5,6 – прямоугольные треугольники – т.С5, С6 (вырезы)
7 – круг R = 7мм (отверстие) – т.С7 (совпадает с т.С1)
2). Выбираем оси координат: ось ОY совместим с осью симметрии сечения, ОХ – проведем по нижней грани сечения.
3). Определяем координаты точек С1, С2, С3, С4,С5, С6, С7 и площади простых фигур.
т.С1:
х1 = 0
y1 = 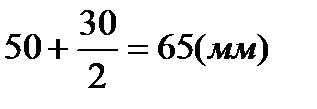
A1 = 80*30 = 2400(мм2)
т.С2:
х2 = 0
y2 = 
A2 = 50*40=2000(мм2)
т.С3,С4:
х3 = 
х3 = 33,3(мм)
y3 = y4 = 
A2 = A3 =  (мм2)
(мм2)
т.С5,С6:
х5 = 
х6 = 16,7(мм)
y5 = y6 = 
A5 = A6 =  (мм2)
(мм2)
т.С7:
x7= 0
y7 = 65(мм)
А7 = ПR2 = 3,14*72 = 153,9(мм2)
4). Определяем координаты центров тяжести сечения:
хс = 0 (т. С лежит на оси симметрии ОY)
yс= 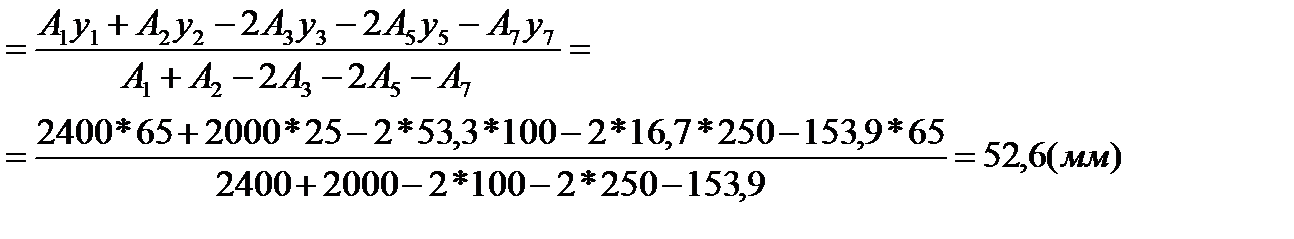
5). т.С (0;52,6(мм))-на сечении.
Пример 3. Определить координаты центра тяжести составного сечения. Показать положение центра тяжести на сечении.
 I№20
I№20
2L50х4
1). Выписываем из таблиц сортамента:
I№20
h = 200мм = 20см
в = 100мм = 10см
d = 5,2мм
t = 8,4мм
А = 26,8см2
L50х4
в = 50мм
d = 4мм
Ζ0 = 1,38 см
А = 3,89 см2
2). Вычерчиваем сечение в масштабе. Указываем центры тяжести профилей:
I №20 – т.С1
L 50,4 – т.С2, С3.
3). Выбираем оси координат. Ось OY совместим с осью симметрии сечения, ОХ проведем через т.С1.
4). Определяем координаты точек С1, С2, С3.
т.С1:
х1 = 0
y1 = 0
A1 = 26,8(см2)
т. С2:
х2 = 
y2 = 
A2 = 3,89(см2)
т.С3:
х3 = 3,62(см)
y3 = y2= 11,38(см)
А3 = А2 = 3,89(см2)
5). Определяем координаты центра тяжести сечения:
хс= 0 (центр тяжести лежит на оси симметрии ОУ)
yс= 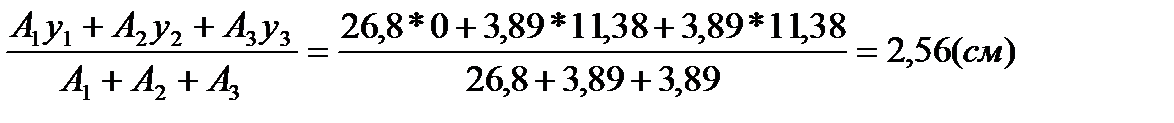
т.С(0; 2,56см) – показываем на сечении.
Пример 4. Определить координаты центра тяжести составного сечения. Показать положение центра тяжести на сечении.

[№22
h = 220мм
в = 82мм
d = 5,4мм
t = 9,5мм
Zo= 2,21см
А = 26,7см2
L110х70х8
В = 110мм = 11см
в = 70мм
d = 8мм
хо = 1,64см
уо = 3,61см
А = 13,9см2
2). Вычерчиваем сечение в масштабе 1:4. Указываем центры тяжести профилей: I №22 – т.С1 и L 110х70х8 – т.С2, С3.
3). Выбираем оси координат. Ось ОХ совместим с осью симметрии через т.С1.
4). Определяем координаты точек С1, С2, С3.
т.С1:
х1 = 0
у1 = 0.
А1 = 26,7см2
т.С2:
х2 = 250мм – Zo– хо = 25см – 2,21см – 1,64см = 21,15(см)
у2 = В – уо = 11см – 3,61см = 7,39(см)
А2 = 13,9см2
т.С3:
х2 = х3 = 21,15(см)
у3 = -у2 = -7,39(см)
А3 =А2 = 13,9(см2)
5). Определяем координаты центра тяжести всего составного сечения:
хс = 
Ус = 0. (т.С лежит на оси симметрии ОХ).
т.С(10,79см; 0) – показываем на сечении.
Центры тяжести площадей простых геометрических фигур.
1). Прямоугольник в х h

2). Прямоугольный треугольник


в – основание
h–высота
в – основание
h–высота
3). Круг. R – радиус
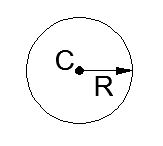
4). Полукруг. R – радиус.


хс = 
ус = 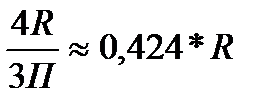 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Муфты компенсирующие упругие | | | Для специальности «Строительство и эксплуатация зданий и сооружений» |
Не нашли, что искали? Воспользуйтесь поиском: