Фиктивные опорные реакции балок.

Задание № 6

для расчётно – графической работы

«Расчёт неразрезных балок»

Для специальности «Строительство и эксплуатация зданий и сооружений»

Примеры расчёта

Преподаватель: Фофанова В.В.

К выполнению задания рекомендуется приступить после изучения тем:

- многопролётные статически неопределимые(неразрезные) балки

- расчёт неразрезных балок с помощью уравнения 3^х моментов.

1. Степень статистической неопределимости, т.е. число «лишних» связей =балки составит:

Л = С_on – 3 = 5 – 3 = 2

2. Выбираем основную систему. Крайнюю левую жесткую опору, представим в виде 3^х опорных стержней с фиктивным пролётом между ними ₁=0.

Нумеруем опоры балки: 0,1,2,3 и пролёты: ₁, ₂, ₃ – слева направо.

Отбросим консоль, заменив её действие моментом от нагрузки на консоли:

М₃ = - q * 2 * 1 = - 4 * 2 * 1 = - 8 (кН * м)

На промежуточные опоры 1 и 2 вводим промежуточные шарниры, разрезав ими балку. Взамен этого слева и справа от опор 1 и 2 прикладываем опорные моменты М₁ и М₂.

Опорные моменты на опорах:

М₀ = 0.

М₁, М₂ – неизвестны.

М₃ = - 8(кН*м).

3. Рассматриваем, пролёты неразрезной балки в основной системе как отдельные однопролётные балки на 2^х шарнирных опорах и определяем для каждого пролёта действительные опорные реакции, фиктивные опорные реакции, строим эпюры Q и M.

Пролет 1 – фиктивный - ₁ = 0. А₁^ф = 0 В₁^ф = 0.

Пролет 2

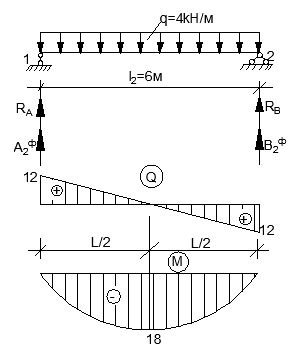
Пользуясь формулой для эпюр Q и M простых балок (см. приложение), получим: R_A = R_B = = = 12 (кН) M_max = 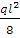= = 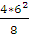18 (кН*м).

Фиктивные опорные реакции (см. приложение): А₂^ф =В₂^ф = = =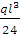

=36(кН* м)

Пролет 3.

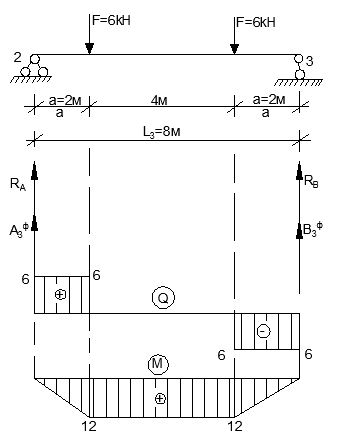
R_A = R_B = F = 6 (кН)

M_max = F * a = 6*2 = 12 (кН*м)

А₃^ф = В₃^ф = 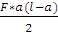= = 36(кН*м)

4. Строим эпюры Q_F⁰ и M_F⁰ – поперечных

сил и изгибающих моментов от действия

нагрузки в основной системе.

5. Чтобы определить неизвестные опорные

моменты М₁ и М₂ для 1 –й и 2-й

промежуточных опор балки

составим уравнение 3^х моментов:

для опоры n:

M_n-1ln + 2M_n( _n + _n+1) + M_{n+1 n+1} = - 6(B_n^ф + А_n+1^ф)

n=1: М_{0 1} + 2М_{1( 1}+ ₂) + М_{2 2} = -6 (B₁^ф + А₂^ф)

0*0 + 2М₁(0+6)+М₂*6 = - 6(0+36)

12М₁+6М₂ = - 216(1)

n=2: М_{1 2} + 2М₂( ₂+ ₃) + M₃l₃ = -6(B₂^ф + А₃^ф)

M₁*6+2M₂(6+8) – 8*8 = - 6(36+36)

6M₁+28M₂ = - 368(2)

Решаем систему: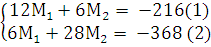

Из (1): М₂ = 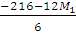= -36 – 2М₁ 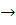во (2)

6М₁ + 28(- 36 – 2М₁) = - 368

6М₁ – 1008 – 56 М₁ = - 368

- 50 М₁ =640

М_{1 =} -12,8 (кН*м)

М₂ = -36 – 2*(-12,8) = - 10,4(кН* м).

Строим эпюру опорных моментов М_оn. Откладываем значения на опорах 0,1,2,3 с учетом знака, в масштабе, соединяем прямыми. Определяем значение в промежуточных точках С,Д,К.

М_с = 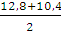= 11,6(кН*м) (-11,6) – середина пролёта 2(средняя линия трапеции.

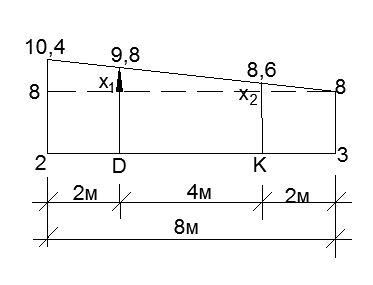Пролёт 3:

Из подобия ∆ - ков:

= ;

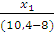X₁ = = 1,8

1,8 + 8 = 9,8 = М_д.

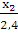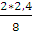= ; x₂ = = 0,6

0,6 + 8 = 8,6 = М_к

Определяем поперечные силы в пролётах по формуле:

Q_n =

Пролёт 2: Q₂ = 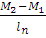= = 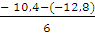0,4 (кН)

Пролёт 3: Q₃ = 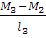= = 0,3 (кН)

Строим эпюру поперечных сил от действия опорных моментов Q_on.

6. Строим окончательные эпюры для всей балки, складывая значения в соответствующих точках с учётом знака на эпюрах:

Q_ок = Q_F⁰ + Q_on

M_ок = M_F⁰ + M_on

Q₁ = 12 + 0,4 = 12,4(кН)

Q_c = 0 +0,4 = 0,4 (кН)

Q₂^лев = - 12 + 0,4 = - 11,6 (кН)

Q₂^прав = 6 + 0,3 = 6,3 (кН)

Q_д^лев = 6+0,3 = 6,3 (кН)

Q_д^прав = 0+0,3 = 0,3(кН)

Q_к^лев = 0 + 0,3 = 0,3 (кН)

Q_к^прав = - 6 + 0,3 = - 5, 7 (кН)

Q_з^лев = - 5,7(кН)

Консоль:

Q_з^прав = q * z = = 0

наклонная прямая = 4 * 2 = 8(кН)

М₁ = 0+(- 12,8) = - 12,8 (кН*м)

М_с = 18 – 11,6 = 6,4 (кН*м)

М₂ = 0 – 10,4 = - 10,4 (кН*м)

М_д = 12 – 9,8 = 2,2 (кН*м)

М_к = 12 – 8,6 = 3,4 (кН* м)

М_з = 0 – 8 = - 8 (кН*м)

Консоль:

М_з^прав = -q *z * = = 0

парабола = - 4*2*1 = -8 (кН*м)

7. Пользуясь эпюрой Q_ок, определяем опорные реакции неразрезной балки по формуле:

R_n = - Q_лев +Q_прав

R₁ = 12,4 (кН)

R₂ = - (- 11,6) +6,3 = 17,9(кН)

R₃ = - (- 5,7) + 8 = 13,7 (кН).

Выполним проверку: ∑F_iy =0?

R₁ + R₂ + R₃ – 2F – q(6+2) = 12,4 + 17, 9 +13, 7 – 2*6 – 4* 8 = 44 – 12 – 32 = 0. (верно).

Определим вершину параболы во 2 –м пролете.

Расстояние слева до вершины – Z₀.

Z₀ -?

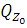^лев = 0. R₁ – q*Z₀ = 0. Z₀ = 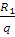= = 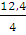3,1 (м)

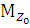^лев= R₁*Z₀ – q*Z₀* 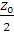+M₁ = 12,4 * 3, 1 – 4*3,1* 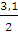– 12,8 = 38,44 – 19, 22 – 12, 8 = 6, 42 (кН*м).

Пример 2. Для неразрезной балки построить эпюры Q и M.

1. Степень статической неопределимости, т.е. число «лишних» связей балки:

Л = С_on - 3 = 5 – 3 = 2

2. Нумеруем опоры балки слева направо: 0,1,2,3. Пролёты: l₁, l₂, l₃. Отбросим консоль, заменив её действие моментом от действия силы F₁ на консоли: (в т. 0):

М₀ = -F₁ * 1,5 = - 2*1,5 = - 3 (кН*м)

Выбираем основную систему, введя промежуточные шарниры на промежуточные опоры балки 1 и 2. Взамен этого слева и справа от опор 1 и 2 прикладываем опорные моменты М₁ и М₂.

Моменты на опорах:

М₀ = - 3кН*м

М₁,М₂ – неизвестны

М₃ = 0

3. Рассматриваем пролёты неразрезной балки как простые однопролётные балки на 2^х шарнирных опорах. Пользуясь формулами для эпюр Q и М простых балок находим действительные опорные реакции фиктивные опорные реакции (см. приложение). Строим эпюры Q и M.

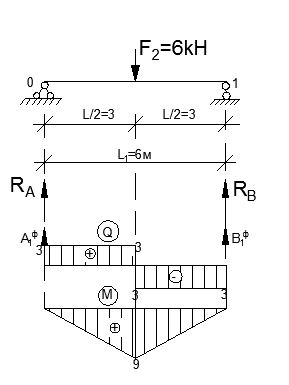Пролёт 1.

R_A = R_B = = = 3(кН)

М_max = = = 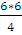9(кН*м)

A₁^ф = В₁^ф = = = 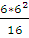13,5 (кН*м)

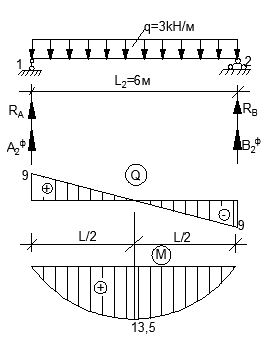Пролет 2.

R_A =R_B = = = 9 (кН)

М_max = 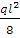= = 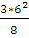13,5 (кН*м)

А₂^ф = В₂^ф = 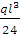= = 27 (кН*м²)

Пролёт 3

R_A=R_B = = = 7,5(кН)

M_max= 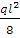= = 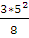9,38 (кН*м)

A₃^ф = В₃^ф = 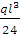= = 15, 625 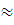15,63(кН* м²)

4. Строим эпюры Q_F⁰ и M_F⁰ – от действия нагрузки в основной системе.

5. Чтобы найти неизвестные опорные моменты М₁ и М₂, составим уравнение 3^х моментов для 1 –й и 2 –й опор:

n = 1

M₀l₁ + 2M₁(l₁+l₂) + M₂l₂ = -6(B₁^ф + А₂^ф)

-3,6 + 2М₁(6+6) + М₂*6 = -6 (13,5 + 27)

-18 +24М₁+6М₂ = -243

24М₁+6М₂ = - 225(1)

n = 2

М₁l₂ + 2M₂(l₂+l₃) +M₃l₃ = - 6(B₂^ф+ А₃^ф)

М₁*6 + 2М₂(6+5) +0*5 = - 6(27+ 15,63)

6М₁ + 22М₂ = - 255,75 (2)

Решаем систему:s w:space="720"/></w:sectPr></w:body></w:wordDocument>">

Из (1): М₂= 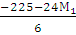= -37, 5 – 4М₁ 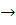во (2)

6М₁+22(-37,5 – 4М₁) = - 255,75

6М₁ – 825 – 88М₁ = - 255,75

- 82М₁ = 569,25 М₁ = - 6,94 (кН*м)

М₂ = - 37, 5 – 4* (- 6,94) = - 9, 74 (кН*м)

Строим эпюру опорных моментов М_on. Откладываем значения на опорах с учётом знака, в масштабе, соединяем прямыми. Определяем значения в промежуточных точках.

М_с = 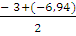= - 4, 97 (кН*м)

М_д = 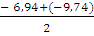= - 8,34 (кН*м)

М_к = 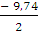= - 4, 87 (кН*м)

Определяем поперечные силы в пролётах по формуле:

Q_n=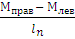

Пролёт 1: Q₁ = 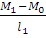= = 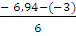- 0, 657 (кН)

Пролёт 2: Q₂ = = = 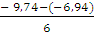- 0, 47 (кН).

Пролёт 3: Q₃ = 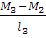= = 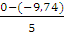1,948 (кН)

Строим эпюру Q_on – поперечных сил от действия опорных моментов, в масштабе, с учётом знака.

6. Строим окончательные эпюры для всей балки, складывая значения в соответствующих точках, с учётом знака, на эпюрах:

Q_OK = Q_F⁰ + Q_on

M_OK = M_F⁰ + M_on

Q_o = 3 – 0, 657 = 2, 343 (кН)

Q_c^лев = 3 – 0,657 = 2, 343 (кН)

Q_c^прав = - 3 – 0,657 = - 3,657 (кН)

Q₁^лев = - 3 – 0,657 = - 3,657 (кН)

Q₁^прав= 9 – 0,47 = 8,53 (кН)

Q_Д = 0 – 0,47 = - 0,47 (кН)

Q₂^лев = - 9 – 0, 47 = - 9, 47 (кН)

Q₂^прав = 7,5 + 1, 948 = 9,448 (кН)

Q_K = 0+ 1,948 = 1,948 (кН)

Q₃ = - 7,5 + 1,948 = - 5, 552(кН)

Консоль: Q₀^лев = -F₁ = - 2 (кН)

M₀ =0 – 3 = - 3 (кН*м)

М_с = 9 – 4, 97 = 4,03 (кН*м)

М₁ = 0 – 6,94 = - 6,94 (кН*м)

М_Д= 13,5 – 8,34 = 5,16(кН*м)

М₂ = 0 – 9,74 = - 9,74 (кН*м)

М_К= 9,38 – 4,87 = 4,51 (кН*м)

М₃ = 0+0=0

Консоль: М₀^лев = - F₁*z= =0

наклонная прямая = - 2*1,5 = - 3(кН*м)

7. Пользуясь эпюрой Q_OK, определяем опорные реакции по формуле:

R_n = - Q_лев + Q_прав

R₀ = -(-2) +2, 343 = 4,343 (кН)

R₁ = - (- 3,657) + 8,53 = 12, 187 (кН)

R₂ = - (- 9,47) + 9,448 = 18, 918 (кН)

R₃ = - (- 5,552) = 5,552 (кН)

Выполняем проверку:

∑F_iy = 0? R₀+R₁+R₂+R₃-F₁-F₂-q*(6+5) = 4,343+12,187+18,918+5,552-2-6-3*11=41-8-33 = 0.(верно)

Определим вершины параболы во 2 – м и 3 – м пролетах.

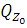^прав = 0. q*Z₀ – R₃ = 0.

Z₀ = 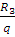= = 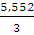1,85 (м)

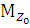^прав = R₃ * Z₀ – q * Z₀ * 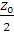= 5, 552 * 1,85 – 3 * 1,85 * = 10, 27 – 5,13 = 5,14 (кН*м)

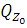-? ^прав = 0. q * Z₀ – R₃ – R₂ = 0.

Z₀ = 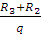= = 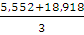8,157 (м)

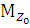^прав = R₃ * Z₀ + R₂(Z₀ – 5) – q * Z₀ * 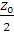= 5,552 * 8, 157 + 18, 918 * 3, 157 – 3 * 8,157 * = 45,288 + 59, 724 – 99, 8 = 5, 212 (кН*м)

Фиктивные опорные реакции балок.

A^ф = В^ф =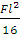

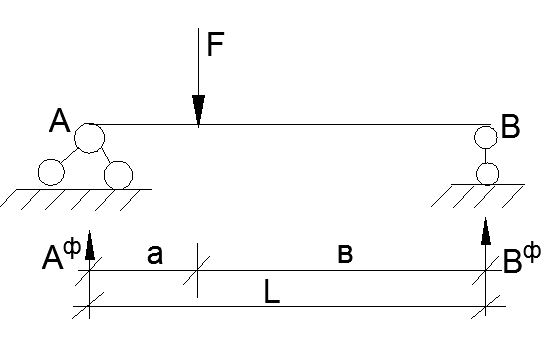
А^ф =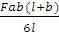

B^{ф =}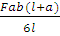

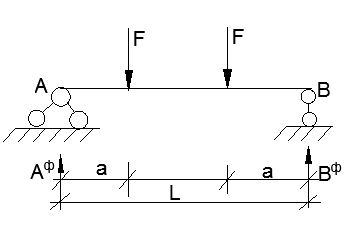
A^ф = В^ф =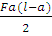

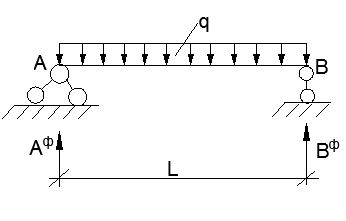
А^ф = В^ф =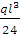

Приложение

Не нашли, что искали? Воспользуйтесь поиском: