Абсолютная и относительная погрешности

На практике обычно числа, над которыми производятся вычисления, являются приближенными значениями тех или иных величин. Для краткости речи приближенное значение величины называют приближенным числом. Истинное значение величины называют точным числом. Приближенное число имеет практическую ценность лишь тогда, когда мы можем определить, с какой степенью точности оно дано, т.е. оценить его погрешность. Напомним основные понятия из общего курса математики.

Обозначим: x - точное число (истинное значение величины), а -приближенное число (приближенное значение величины).

Определение 1. Погрешностью (или истинной погрешностью) приближенного числа называется разность между числом x и его приближенным значением а. Погрешность приближенного числа а будем обозначать . Итак,

.

(1.1)

Погрешность может быть числом положительным, отрицательным или равным нулю.

Определение 2. Абсолютной погрешностью приближенного числа а называется модуль разности между числом х и его приближенным значением а.

Абсолютную погрешность приближенного числа а будем обозначать , т.е.

.

(1.2)

Точное число x чаще всего бывает неизвестно, поэтому найти истинную и абсолютную погрешности не представляет возможным. С другой стороны, бывает необходимо оценить абсолютную погрешность, т.е. указать число, которого не может превысить абсолютная погрешность. Например, измеряя длину предмета данным инструментом, мы должны быть уверены в том, что погрешность полученного числового значения не превысит некоторого числа, например 0,1 мм. Другими словами, мы должны знать границу абсолютной погрешности. Эту границу будем называть предельной абсолютной погрешностью.

Определение 3. Предельной абсолютной погрешностью приближенного числа а называется положительное число такое, что , т.е.

.

(1.3)

Из формулы (1.3) получаем:

(1.4)

Значит, есть приближенное значение числа х по недостатку, - по избытку. Применяют также такую запись:

.

(1.5)

Ясно, что предельная абсолютная погрешность определяется неоднозначно: если некоторое число есть предельная абсолютная погрешность, то любое большее число тоже есть предельная абсолютная погрешность. На практике стараются выбирать возможно меньшее и простое по записи (с 1-2 значащими цифрами) число , удовлетворяющее неравенству (1.3).

Пример. Определить истинную, абсолютную и предельную абсолютную погрешности числа а = 0,17, взятого в качестве приближенного значения числа .

Истинная погрешность:

Абсолютная погрешность:

За предельную абсолютную погрешность можно принять число и любое большее число. В десятичной записи будем иметь: Заменяя это число большим и возможно более простым по записи, примем:

Замечание. Если а есть приближенное значение числа х, причем предельная абсолютная погрешность равна h, то говорят, что а есть приближенное значение числа х с точностью до h.

Знания абсолютной погрешности недостаточно для характеристики качества измерения или вычисления. Пусть, например, получены такие результаты при измерении длины. Расстояние между двумя городами S₁ =500 1 км и расстояние между двумя зданиями в городе S₂ =10 1 км. Хотя абсолютные погрешности обоих результатов одинаковы, однако существенное значение имеет то, что в первом случае абсолютная погрешность в 1 км приходится на 500 км, во втором - на 10 км. Качество измерения в первом случае лучше, чем во втором. Качество результата измерения или вычисления характеризуется относительной погрешностью.

Определение 4. Относительной погрешностью приближенного значения а числа х называется отношение абсолютной погрешности числа а к абсолютному значению числа х:

.

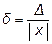(1.6)

Так, как точное число обычно бывает неизвестно, его заменяют приближенным числом:

.

(1.7)

Определение 5. Предельной относительной погрешностью приближенного числа а называется положительное число такое, что _.

Так как 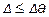, то из формулы (1.7) следует, что можно вычислить по формуле

.

(1.8)

Для краткости речи в тех случаях, когда это не вызывает недоразумений, вместо “предельная относительная погрешность” говорят просто “относительная погрешность”.

Предельную относительную погрешность часто выражают в процентах.

Пример 1. . Полагая , можем принять = . Производя деление и округляя (обязательно в сторону увеличения), получим =0,0008=0,08%.

Пример 2. При взвешивании тела получен результат: p=23,4 0,2 г. Имеем =0,2. . Производя деление и округляя, получим =0,9%.

Формула (1.8) определяет зависимость между абсолютной и относительной погрешностями. Из формулы (1.8) следует:

.

(1.9)

Пользуясь формулами (1.8) и (1.9), мы можем, если известно число а, по данной абсолютной погрешности находить относительную погрешность и наоборот.

Заметим, что формулы (1.8) и (1.9) часто приходится применять и тогда, когда мы еще не знаем приближенного числа а с требуемой точностью, а знаем грубое приближенное значение а. Например, требуется измерить длину предмета с относительной погрешностью не выше 0,1%. Спрашивается: возможно ли измерить длину с нужной точностью при помощи штангенциркуля, позволяющего измерить длину с абсолютной погрешностью до 0,1 мм? Пусть мы еще не измеряли предмет точным инструментом, но знаем, что грубое приближенное значение длины - около 12 см. По формуле (1.9) находим абсолютную погрешность:

мм

Отсюда видно, что при помощи штангенциркуля возможно выполнить измерение с требуемой точностью.

В процессе вычислительной работы часто приходится переходить от абсолютной погрешности к относительной, и наоборот, что делается с помощью формул (1.8) и (1.9).

Не нашли, что искали? Воспользуйтесь поиском: