
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Ошибки, содержащиеся в исходной информации
Эти ошибки возникают в результате неточности измерений или из-за невозможности представить необходимую величину (например, число  ) конечной дробью.
) конечной дробью.
Никакое физическое измерение невозможно выполнить абсолютно точно. Если, например, указано, что величина напряжения в электрической цепи составляет 125.4873596 В, то можно с уверенностью сказать, что по меньшей мере 5 младших значащих цифр недостоверны, т.к. не существует вольтметров, способных проводить измерения одновременно в столь широких пределах и с такой высокой точностью.
С другой стороны, если экспериментальный результат содержат небольшое количество значащих цифр (например, длительность импульса в 1.3 сек), то можно быть абсолютно уверенным, что эта величина дана с некоторой ошибкой. В таких случаях подразумеваются некоторые границы, внутри которых эта величина может находиться, например, 2,3  0,1 сек.
0,1 сек.
Обычно подразумевается, что если для результата измерения не указаны возможные границы, то результат имеет точность, равную половине единицы младшего разряда. Например, если результат измерения равен 6.63 мм, то следует понимать, что эта длина не меньше 6.625 мм и не больше 6.635 мм.
Многие числа, фигурирующие в качестве исходной информации в каких-либо вычислительных формулах, нельзя представить точно ограниченным количеством значащих цифр. Например, число  можно представить в виде 3.14, или 3.141592, или 3,141592653589793 в зависимости от того, какая точность требуется в данном конкретном вычислении. Но в любом случае это представление будет неточным, т.к
можно представить в виде 3.14, или 3.141592, или 3,141592653589793 в зависимости от того, какая точность требуется в данном конкретном вычислении. Но в любом случае это представление будет неточным, т.к  - число иррациональное. То же самое относится и к многим рациональным числам, т.к. большая их часть выражается хоть и периодической, но все-таки бесконечной десятичной дробью, например,
- число иррациональное. То же самое относится и к многим рациональным числам, т.к. большая их часть выражается хоть и периодической, но все-таки бесконечной десятичной дробью, например, 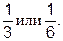 Т.к. в настоящее время большинство расчетов ведется на ЭВМ, то здесь следует отметить, что дроби, являющиеся конечными в одной системе счисления, например, в десятичной, оказываются бесконечными в другой, например, в двоичной: дробь
Т.к. в настоящее время большинство расчетов ведется на ЭВМ, то здесь следует отметить, что дроби, являющиеся конечными в одной системе счисления, например, в десятичной, оказываются бесконечными в другой, например, в двоичной: дробь 
 явно имеет конечное десятичное представление - 0.1, но при переводе в двоичную систему представляется бесконечной периодической дробью 0.0001100110011001100... Если на ЭВМ вычислить сумму тысячи таких чисел, то результат окажется не равным 100.
явно имеет конечное десятичное представление - 0.1, но при переводе в двоичную систему представляется бесконечной периодической дробью 0.0001100110011001100... Если на ЭВМ вычислить сумму тысячи таких чисел, то результат окажется не равным 100.
Начинающих такие “чудеса” иногда приводят в замешательство.
Следует отметить еще один источник ошибок, содержащихся в исходной информации. Это грубые ошибки, возникающие из-за опечаток, описок, неверного съема показаний. Обязательно надо иметь в виду, что, если для какой-либо обработки представлен числовой массив достаточно большого объема (100-1000), то очень велика вероятность того, что в этом массиве по крайней мере одно-два числа будут неверными, ошибочными.
Ошибки, содержащиеся в исходной информации, определяют точность результата независимо от того, каким методом эти вычисления производятся. Два других типа ошибок - ошибки ограничения и ошибки округления - определяются теми методами, которые были использованы для решения задачи.
Ошибки ограничения
Для демонстрации «ошибки ограничения» рассмотрим вычисление функции 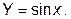 Вычисление этой функции производится с помощью следующего ряда Тейлора
Вычисление этой функции производится с помощью следующего ряда Тейлора

Как видно, ряд - бесконечный. Естественно, что невозможно в практических вычислениях вести счет бесконечно. Вычисления ограничиваются конечным числом членов ряда, например, до x 7 или x 9. Отброшенные члены ряда, а их количество бесконечно, вносят некоторую ошибку в результат вычислений. Эта ошибка и называется ошибкой ограничения, т.к. она возникает в результате ограничения бесконечного вычислительного процесса.
Надо отметить, что очень многие вычислительные методы приводят к бесконечным математическим процессам, поэтому анализ ошибок ограничения очень важен.
Ошибки округления
Даже, если предположить, что исходная информация не содержит никаких ошибок, а все вычислительные процессы конечны, то все равно и в этом случае присутствует третий тип ошибок - ошибки округления.
Предположим, что вычисления производятся на машине, в которой каждое число может представляться не более, чем пятью значащими цифрами (отличать от термина «пять знаков после запятой»), например, 15735, 23.749, 0.16783, 0.000093436. Пусть необходимо сложить два числа 9.2654 и 7.1625, причем эти два числа являются точными. Точное значение этой суммы равно 16.4279, но оно содержит 6 значащих цифр и потому не помещается в разрядной сетке нашей гипотетической машины. Поэтому результат будет округлен до 16.428 и при этом возникнет ошибка округления.
Так как ЭВМ всегда работает с конечным количеством значащих цифр, то округление результатов арифметических операций производится очень часто. Для изучения округления действительных чисел необходимо рассмотреть форму представления таких чисел в памяти ЭВМ.
Для представления вещественных чисел используется так называемая форма «с плавающей точкой», в которой число записывается через мантиссу и порядок 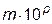 . Например, число 5.673 в виде с плавающей точкой можно записать так:
. Например, число 5.673 в виде с плавающей точкой можно записать так:
56.73.10-1, или 5.673.101, или 0.5673.102, или 0.05673.103 и т.д.,
т.е. для одного и того же числа можно записать много форм его представления с плавающей точкой. Среди всех этих представлений есть одно, особенное, называемое нормализованным. Для нормализованного представления выполняется:
0,1  <1,
<1,
т.е. целая часть мантиссы равна нулю, а дробная часть в старшем разряде содержит любую цифру кроме нуля.
Рассмотрим процесс сложения двух чисел А=162.45 и В=1.7698 в нашей гипотетической 5-разрядной ЭВМ. В нормализованном представлении с плавающей точкой
А=0.16245.103, В=0,17698.101.
Сначала происходит выравнивание порядков:
А = 0.1624500.103,
В = 0.0017698.103,
затем сложение мантисс:
А+В = 0.1642198.103.
В этой записи дробная часть мантиссы содержит не 5, а 7 значащих цифр, следовательно, последние две должны быть отброшены. Отбрасываемая часть суммы равна 0.98.10-2. Такое отбрасывание должно производиться, естественно, с округлением старшей части результата.
Существуют и практически реализуются несколько правил округления.
Простейший способ - отбрасывание младшей части результата
А+В = 0.16421.103 = 164.21.
Этот метод так и называется: отбрасывание младших разрядов.
Более общепринятый способ - симметричное округление.
Обозначим результат сложения так:
 ,
,
где  - старшая часть результата;
- старшая часть результата;  - младшая часть результата;
- младшая часть результата;
p - порядок результата; q - количество значащих цифр в представлении числа.
(В нашем случае F=0.16421.103, G=0.98.103-5=0.98.10-2, p=3, q=5)
Тогда симметричное округление выполняется по правилу: результат  с округлением равен
с округлением равен
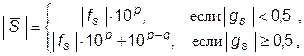
 .
.
(В нашем случае gs =0.98≥0.5, поэтому  =0.16421.103+10-2=0.16422.103=164.22.)
=0.16421.103+10-2=0.16422.103=164.22.)
Иногда применяется более точное правило округления, учитывающее  .
.
Относительная ошибка округления, выполненного способом отбрасывания, выражается формулой  . Это, естественно, самая грубая ошибка из всех способов округления.
. Это, естественно, самая грубая ошибка из всех способов округления.
Относительная ошибка симметричного округления:  , т.е. ошибка симметричного округления в среднем в два раза меньше ошибки отбрасывания.
, т.е. ошибка симметричного округления в среднем в два раза меньше ошибки отбрасывания.
В старших поколениях ЭВМ, характеризуемых сравнительно низким быстродействием, применялся в основном алгоритм отбрасывания. В современных ЭВМ, особенно если они оснащаются сопроцессорами вещественной арифметики, применяется симметричное округление. Округление, учитывающее случай  , в ЭВМ практически не применяется, так как оно требует большего времени без существенного увеличения точности.
, в ЭВМ практически не применяется, так как оно требует большего времени без существенного увеличения точности.
Следует учесть, что современные ЭВМ работают в двоичной системе счисления. Поэтому нормализованное представление чисел с плавающей точкой выглядит так:
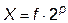 ,
, 
Поэтому ошибка отбрасывания:  ; ошибка симметричного округления:
; ошибка симметричного округления: 
Анализ ошибок и их распространения при выполнении «длинных» вычислений позволил сформулировать следующие рекомендации по снижению ошибок вычислений:
1. Если необходимо произвести сложение - вычитание длинной последовательности чисел, то надо работать сначала с наименьшими по модулю числами.
2. Если возможно, необходимо избегать вычитания почти равных чисел, т.к. это приводит к большим относительным ошибкам.


Не нашли, что искали? Воспользуйтесь поиском: