Задания контрольной работы

1. В партии из изделий изделий имеют скрытый дефект (табл. 1). Какова вероятность того, что из взятых наугад изделий изделий являются дефектными?
2. На сборочное предприятие поступили однотипные комплектующие с трех заводов в количестве: с первого завода, со второго, с третьего (табл. 2). Вероятность качественного изготовления изделий на первом заводе , на втором , на третьем . Какова вероятность того, что взятое случайным образом изделие будет качественным?
3. Дано распределение дискретной случайной величины (табл. 3). Найти математическое ожидание и среднее квадратичное отклонение.
4. В городе имеется оптовых баз (табл. 4). Вероятность того, что товар требуемого сорта отсутствует на этих базах одинакова и равна . Составить закон распределения числа баз, на которых искомый товар отсутствует в данный момент.
5. Непрерывная случайная величина имеет нормальное распределение. Ее математическое ожидание равно , среднее квадратичное отклонение равно (табл. 5). Найти вероятность того, что в результате испытания случайная величина примет значение в интервале .
6. Найти линейную среднеквадратичную регрессию случайной величины на случайную величину на основе заданного закона распределения двумерной случайной величины (табл. 6).
7. По выборке (табл. 7) построить вариационный ряд. Определить размах выборки, выборочную среднюю, моду и медиану.
8. Рассчитать и построить гистограмму относительных частот по сгруппированным данным (табл. 8), где - частота попадания вариант в промежуток .
9. Найти несмещенную выборочную дисперсию на основании данного распределения выборки (табл. 9).
10. При уровне значимости проверить гипотезу о равенстве дисперсии двух нормально распределенных случайных величин и на основе выборочных данных (табл. 10) при альтернативной гипотезе .

Таблица 1.

Вариант

Таблица 2.

Вариант
		0,9		0,8		0,7
		0,8		0,7		0,7
		0,9		0,7		0,9
		0,7		0,9		0,8
		0,9		0,8		0,6
		0,8		0,8		0,9
		0,8		0,9		0,8
		0,7		0,8		0,9
		0,9		0,8		0,9
		0,8		0,7		0,8
		0,9		0,9		0,8

Таблица 3.

Вариант	Числовые данные
		-5
	0,4	0,3	0,1	0,2
		0,2	0,5	0,6	0,8
	0,1	0,5	0,2	0,2
		-6	-2
	0,1	0,3	0,4	0,2
		0,2	0,5	0,6
	0,5	0,4	0,1
		-8	-2
	0,1	0,3	0,4	0,2
		-2
	0,1	0,3	0,4	0,2
		-3
	0,3	0,4	0,1	0,2
	0,1	0,4	0,5
		-4	-1
	0,3	0,1	0,4	0,2
		-3
	0,3	0,4	0,1	0,2
		-6	-2
	0,2	0,4	0,1	0,3

Таблица 4.

Вариант
		0,2
		0,25
		0,1
		0,2
		0,1
		0,2
		0,3
		0,1
		0,12
		0,3
		0,15

Таблица 5.

Вариант

Таблица 6.

Вариант	Числовые данные
	0,16	0,10	0,28
	0,14	0,20	0,12
	0,06	0,18	0,24
	0,12	0,13	0,27
	0,12	0,24	0,22
	0,20	0,15	0,07
	0,16	0,10	0,28
	0,14	0,20	0,12
	0,06	0,18	0,24
	0,12	0,13	0,27
	0,16	0,10	0,28
	0,14	0,20	0,12
	0,12	0,13	0,24
	0,18	0,06	0,27
	0,06	0,18	0,24
	0,12	0,13	0,27
	0,12	0,13	0,24
	0,18	0,06	0,27
	0,13	0,24	0,12
	0,18	0,06	0,27
	0,13	0,24	0,12
	0,18	0,06	0,27

Таблица 7.

Таблица 8.

Вариант
		2-4
	4-6
	6-8
	8-10
	10-12
		3-7
	7-11
	11-15
	15-19
	19-23
		4-8
	8-12
	12-16
	16-20
	20-24
		4-6
	6-8
	8-10
	10-12
	12-14
		1-5
	5-9
	9-13
	13-17
	17-21
		10-14
	14-18
	18-22
	22-26
	26-30
		3-5
	5-7
	7-9
	9-11
	11-13
		4-9
	9-14
	14-19
	19-24
	24-29
		4-10
	10-16
	16-22
	22-28
	28-34
		5-7
	7-9
	9-11
	11-13
	13-15
		11-14
	14-17
	17-20
	20-23
	23-26

Таблица 9.

Вариант	Распределение
		-6	-2
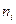
		-10	-5	-1
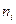
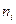
		-3
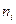
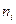
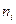
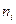
		-4	-1
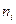
		-6	-2

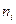
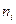
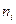
Таблица 10.

Вариант
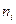
	0,2		0,4
0,4		0,5
0,8		0,9
1,0		1,2
1,2		1,4
	3,5		3,6
3,7		3,7
3,9		3,8
4,0		4,4
4,1		4,2

Не нашли, что искали? Воспользуйтесь поиском: