
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
По выполнению контрольной работы № 2
В данной контрольной работе две задачи №№1-20 относятся к разделу «Сопротивление материалов» и 3 задачи №№21-50 к разделу «Детали машин»
Раздел «Сопротивление материалов»
Основная задача науки "Сопротивление материалов" - оценка прочности, жесткости и устойчивости элементов конструкций. Элемент считается достаточно прочным, если максимальные расчетные напряжения в опасном сечении меньше предельных напряжений в определенное число раз.
Число, показывающее, во сколько раз максимальные расчетные напряжения меньше предельных для материала рассчитываемой детали, называется коэффициентом запаса прочности детали или просто запасом прочности и обозначается n. Деталь прочная в том случае, если запас прочности не меньше требуемого (нормативного) запаса, который обозначается [n]. Он зависит от ответственности детали, срока службы, точности расчета и других факторов. Таким образом, условие прочности записывается в таком виде: n 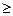 [n]. Часто условие прочности записывают через допускаемые напряжения [σ]. Допускаемыми напряжениями называются максимальные значения напряжений, которые можно допустить при работе конструкции. При этом будет гарантироваться прочность детали:
[n]. Часто условие прочности записывают через допускаемые напряжения [σ]. Допускаемыми напряжениями называются максимальные значения напряжений, которые можно допустить при работе конструкции. При этом будет гарантироваться прочность детали:
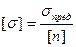
Условие прочности через допускаемые напряжения имеет вид
σпред  [σ]. Незначительное превышение расчетных напряжений - в пределах 5% считается неопасным.
[σ]. Незначительное превышение расчетных напряжений - в пределах 5% считается неопасным.
В расчетах на жесткость определяют максимальные перемещения, соответствующие данному виду нагружения, и сравнивают с допускаемым значением перемещения. Жесткость элемента считается обеспеченной, если максимальное перемещение не превышает допускаемого.
Под устойчивостью детали понимается способность детали сохранять первоначальную форму равновесия при действии заданных нагрузок.
В зависимости от постановки задачи, ее исходных данных существуют три вида расчетов на прочность, жесткость и устойчивость: проверочный, проектный и определение допускаемой нагрузки.
Определяя из условия прочности и жесткости необходимые размеры рассчитываемой детали, можно получить два значения размера. В качестве окончательного следует выбрать больший. Независимо от вида деформации расчет на прочность можно схематично представить в виде следующих этапов:
1 Отыскивается опасное сечение рассчитываемого элемента. Для чего с помощью метода сечений строят эпюры внутренних силовых факторов, соответствующих данному виду нагружения.
2 Зная закон распределения напряжений по площади поперечного сечения при данном виде нагружения, определяют напряжения в опасной точке.
3 Для опасной точки записывают условие прочности, а затем в зависимости от исходных данных задачи производят один из указанных выше расчетов на прочность.
Приступая к выполнению контрольной работы № 2, необходимо понимать, что внутри любого материала имеются внутренние межатомные силы, наличие которых определяет способность тела воспринимать действующие на него внешние силы, сопротивляться разрушению, изменению формы и размеров.
Приложение к телу внешней нагрузки вызывает изменение внутренних сил, т.е. появление дополнительных внутренних сил. В сопротивлении материалов изучают дополнительные внутренние силы, поэтому под внутренними силами понимают силы взаимодействия между отдельными элементами, возникающие под действием внешних сил.
Это понятие равносильно допущению об отсутствии в теле внутренних сил до приложения к нему внешних нагрузок.
Следует напомнить, что в число внешних сил входят как заданные активные силы, так и реакции связей.
Внутренние силы определяют при помощи метода сечений.
Легко запомнить все пункты метода сечений, если записать их словом "РОЗУ" (рисунок 24).
Каждая буква этого слова означает содержание определенной операции этого метода:
- Р - разрезаем тело плоскостью на две части;
- О - отбрасываем одну часть;
- 3 - заменяем действие отброшенной части внутренними силами;
-У- уравновешиваем оставшуюся часть и из уравнений равновесия определяем внутренние силы.
В общем случае нагружения тела внутренние силы, возникающие в поперечном сечении нагруженного бруса, могут быть заменены их статическими эквивалентами - главным вектором и главным моментом. Если последние разложить по осям координат, то получим шесть составляющих с общим названием "внутренние силовые факторы":
N – продольная сила
Q – поперечная сила
Ми – изгибающий момент
Т – крутящий момент
Каждому из внутренних усилии соответствует определенный вид деформации бруса.
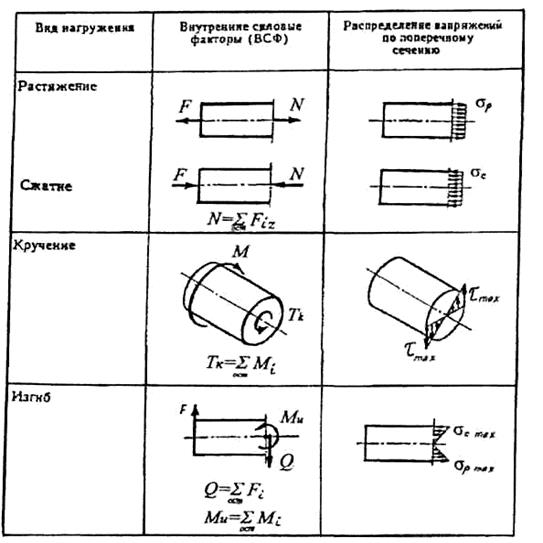
Продольной силе N - соответствует растяжение или сжатие, поперечной силе Q - сдвиг, моменту Тк - кручение, моменту Ми - изгиб. Различные их сочетания представляют собой случаи сложного сопротивления.

|
Ось Z – продольная ось,
Оси X,Y – поперечные оси
|
Рисунок 24

|
Внутренние силы, распределенные по поверхности, характеризуются их интенсивностью.
Интенсивность поперечных сил в рассматриваемой точке сечения называется касательными напряжениями и обозначается τ (тау), а интенсивность нормальных сил - нормальными напряжениями и обозначается σ (сигма).
Нормальные и касательные напряжения являются составляющими полных напряжений

Нормальные напряжения в данной точке по определенному сечению характеризует интенсивность сил отрыва или сжатия, расположенных по обе стороны этого сечения.
Касательные напряжения - интенсивность сил, сдвигающих эти частицы в плоскости рассматриваемого сечения.
При практических расчетах, связанных с определением напряжений в сечениях бруса вместо единицы напряжений 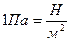 напряжения имеют размерность
напряжения имеют размерность 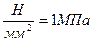 .
.
Задачи №№ 1-10
К решению этих задач следует приступить после изучения темы 2.2 "Растяжение, сжатие" и внимательного изучения примера 15.
В конструкциях подвижного состава имеются элементы, работающие на растяжение или сжатие (иногда попеременно растяжение-сжатие). К ним относятся автосцепка, поводок буксы, элементы подвески экипажной части локомотивов, поршень и шток в цилиндре дизеля локомотива и автомобиля и др.
Формы и размеры этих элементов конструкций определяются необходимостью обеспечить их прочность при действии растягивающих или сжимающих усилий, возникающих в процессе работы подвижного состава.
Растяжением (сжатием) называют такое нагружение бруса, при котором в поперечных сечениях возникает только один внутренний силовой фактор - продольная сила N.
Продольную силу определяем при помощи метода сечений.
Продольная сила N в любом поперечном сечении бруса численно равна алгебраической сумме проекций на продольную ось z всех внешних сил, действующих на оставшуюся часть бруса.
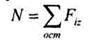
Правило знаков: условимся внешние силы, растягивающие брус, считать положительными, а сжимающими его - отрицательными.
По известной продольной силе N и площади поперечного сечения А можно определить напряжения в этом сечении:
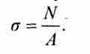
Условие прочности при растяжении и сжатии имеет вид
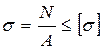 р
р
где: σ – наибольшие по абсолютной величине расчётные нормальные напряжения при растяжении, сжатии;
[σ]р – допускаемые напряжения при растяжении, сжатии;
А – площадь поперечного сечения;
N – продольная сила в опасном сечении.
Изменение длины бруса равно алгебраической сумме удлинений (укорочений) его отдельных участков и вычисляется по формуле Гука:
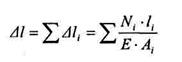
Пример 15
Для заданного на рисунке 25 бруса построить эпюры продольных сил и нормальных напряжений, проверить прочность на II и V участках, приняв [σ]р =160 МПа, [σ]с = 120 МПа, а также определить перемещение свободного конца, если модуль продольной упругости Е = 2 . 105 МПа. Вес бруса не учитывать.

Рисунок 25
Решение
1 Разделим брус на участки, границы которых определяются
местами изменения поперечных размеров бруса и точками приложения внешних нагрузок.
Рассматриваемый брус имеет пять участков.
Для закрепленного одним концом бруса расчет целесообразно вести со свободного конца, чтобы не определять опорной реакции.
2 Применяя метод сечений, определяем значение продольной силы N на каждом участке, выражая ее через внешние силы F1, F2 и F3.
N1 =0
N2 = F1 = 30 кН
N3 = F1 = 30 кН
N4 = F1 – F2 = 30 – 54 = - 24 кН
N5 = F1 – F2 – F3 = 30 – 54 – 5 – 29 кН
Знак плюс показывает, что брус на II и III участках растянут. Отрицательное значение N4 и N5 показывает, что на участках IV и V брус сжат.
По полученным из расчета данным строим эпюру N, показанную на рисунке 25а.
Для этого параллельно оси бруса проведем базовую (нулевую) линию эпюры, откладываем перпендикулярно ей в произвольном масштабе полученные значения N. В пределах каждого участка нагружения продольная сила постоянная, а потому на эпюре изображается прямой, параллельной базовой. Положительные значения будем откладывать вверх от базовой линии, а отрицательные - вниз. Эпюра штрихуется линиями, перпендикулярными оси эпюры.
Эпюра продольных сил представляет собой график, выражающий закон изменения продольной силы во всей длине бруса.
Любая ордината эпюры продольных сил, измеренная в соответствующем масштабе, выражает величину продольной силы в данном поперечном сечении.
3 Вычисляем значения нормальных напряжений:

|
В соответствии с полученными значениями напряжений строим эпюру
нормальных напряжений, она изображена на рисунке 25 б.
При построении эпюр и проверке их правильности следует руководствоваться следующими правилами:
- скачки на эпюрах N имеют место в точках приложения сосредоточенных сил. Величина скачка равна величине внешней силы, приложенной в этом сечении.
- на эпюре σ скачки имеют место не только в точках приложения сосредоточенных сил, но и в местах изменения площади поперечного сечения.
- знаки на участках эпюры σ должны совпадать со знаками на соответствующих участках эпюры N.

|
4 Выполняем проверку прочности бруса, т.е. расчетное напряжение (для каждого участка в отдельности) сравниваем с допускаемыми:
На втором участке имеет место перегрузка. Определим процент перегрузки:
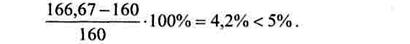
Величины превышений от допускаемых напряжений в пределах 5% в реальном проектировании считаются возможными. Перегрузка не превышает 5%, ГОСТом это допускается.
V участок:

На V участке имеет место недогрузка. Определим процент недогрузки:
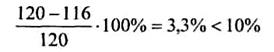
Недогрузка меньше 10%, что допустимо по ГОСТу. Если на каком либо участке недогрузка составляет больше 10%, то сечение выбрано не экономично, имеет место большой перерасход материала.
5 Определяем перемещение свободного конца. Полное удлинение (укорочение) можно найти, воспользовавшись эпюрой N, представленной на рисунке 25а, т.е. полное удлинение бруса равно алгебраической сумме удлинений его участков:
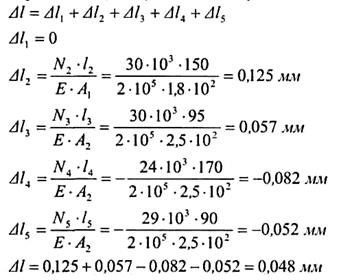
Полученный в ответе знак плюс говорит о том, что в целом брус удлинился, т.е. свободный конец переместился в нашем случае вправо.
Задачи №№11-20
Задачи 11-20 следует решать после изучения темы 2.6 "Изгиб" и внимательного разбора примеров 18, 19.
На изгиб работают большинство элементов кузова, рамы, валы в передачах и др. Прочность элементов, работающих на изгиб обеспечивается правильным подбором формы и размеров сечения.
Прямым поперечным изгибом называется такой вид нагружения, при котором в поперечном сечении бруса возникают два внутренних силовых фактора: поперечная сила Q; изгибающий момент Ми.
Поперечная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций внешних сил, действующих на оставшуюся часть:
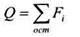 Изгибающий момент Ми в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на оставшуюся часть, относительно центра тяжести сечения:
Изгибающий момент Ми в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внешних сил, действующих на оставшуюся часть, относительно центра тяжести сечения:

Здесь имеется в виду, что все внешние силы и моменты действуют в главной продольной плоскости бруса, причем силы расположены перпендикулярно продольной оси.
Для определения опасного сечения строят эпюры Q и Ми, используя метод сечений.
Правило знаков для поперечной силы
Внешние силы, поворачивающие оставшуюся часть балки относительно рассматриваемого сечения по ходу часовой стрелки, считаем положительными, а силы, поворачивающие оставшуюся часть балки относительно рассматриваемого сечения против часовой стрелки, считаем отрицательными (рисунок 28а).
Правило знаков для изгибающих моментов.
Внешние моменты, изгибающие мысленно закрепленную в рассматриваемом сечении отсеченную часть бруса выпуклостью вниз, считаем положительными, а моменты, изгибающие отсеченную часть бруса выпуклостью вверх (рисунок 28 б) - отрицательными.
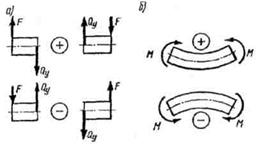
|
Рисунок 28
Условие прочности для балок, работающих на изгиб, имеет вид:
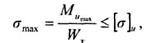
где σmax - максимальные нормальные напряжения;
Wx - осевой момент сопротивления сечения изгибу относительно оси, перпендикулярной плоскости действия Ми;
Ми - абсолютное значение наибольшего изгибающего момента;
[σ]и - допускаемые напряжения.
Пример 18
Для заданной консольной балки, изображенной на рисунке 29, построить эпюры поперечных сил и изгибающих моментов. Подобрать сечение балки в виде двутавра, если [σ]и = 160 МПа.
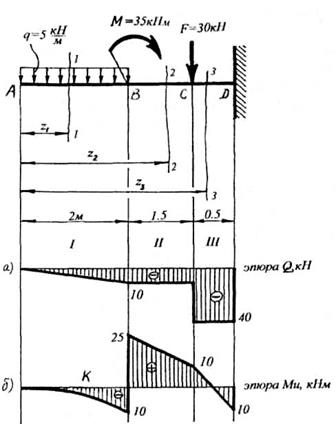
Рисунок 29
Решение
Разбиваем балку на участки. Границы участков целесообразно проводить через точки приложения сосредоточенных сил, моментов, начала и конца равномерно распределенной нагрузки.
Построение эпюр Q и Ми будем вести от свободного конца, чтобы не определять реакции опор.
Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо мысленно рассечь плоскостью в этом месте балку и правую часть балки отбросить.
Затем по действующим на оставленную часть балки внешним нагрузкам надо найти искомые значения Qy и Мх, причем знак их надо определить по тому действию, какое оказывают внешние силы на оставленную часть балки в соответствии с принятым ранее правилом знаков.
1 Построение эпюры поперечных сил (рисунок 29а).
Проводим сечение 1 -1
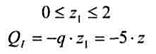
Так как Q1 = f(z1) является уравнением прямой линии, для построения которой нужны 2 точки:
при z1 = 0 QA =0
при z1 = 2 QВ = -q . 2 = - 5 . 2 = - 10 кН
Проводим базовую линию эпюры Q. Перпендикулярно к ней в выбранном масштабе откладываем ординаты, соответствующие значениям
z1 = 0 и z2 = 2 м.
Через 2 полученные точки проводим прямую линию, которая представляет эпюру Q на первом участке.
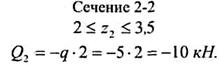
Так как поперечная сила в пределах второго участка является величиной постоянной, поэтому эпюра Q на втором участке представляется прямой, параллельной базовой линии.
Сечение 3-3
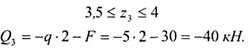
Эпюра на участке III представляется также прямой параллельной базовой линии.
2 Построение эпюры изгибающих моментов (рисунок 29 б).
Сечение 1-1
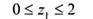
|
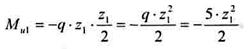
В это уравнение переменная величина z1 входит в квадрате, поэтому зависимость Mu(z1) графически изображается квадратичной параболой.
Для построения параболы нужно как минимум три точки.

Проводим базовую линию эпюры Ми и в выбранном масштабе откладываем ее ординаты соответствующие, значениям z1 = 0; z1 = 1 м;
z1 = 2 м. Соединяем точки, получаем квадратичную параболу, направленную выпуклостью навстречу нагрузке с вершиной в т. А.
В дальнейшем при построении эпюр изгибающих моментов полезно помнить, что квадратичная парабола своей выпуклостью всегда обращена навстречу распределенной нагрузке.
Сечение 2-2
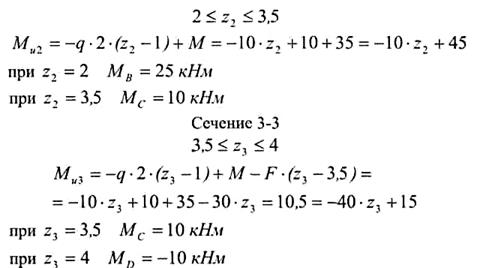
Эпюра изгибающих моментов на участках 2 и 3 представлена наклонными прямыми.
Для построения эпюр необходимо запомнить следующие правила:
- На участке балки, где отсутствует распределенная нагрузка, эпюра Q - прямая, параллельная базовой линии, а эпюра Ми - наклонная прямая (участки 2 и 3).
- В точках, где приложена сосредоточенная сила на эпюре Q наблюдается скачок, численно равный приложенной внешней силе, а на эпюре Ми - излом (точка С).
- В точке приложения сосредоточенного момента на эпюре моментов происходит скачок на величину момента, приложенного в этой точке, а эпюра Q не претерпевает изменения (точка В).
- На участке действия равномерно распределенной нагрузки эпюра Q выражается наклонной прямой, а эпюра Ми - параболой, обращенной выпуклостью навстречу действию распределенной нагрузки (участок 1).
- Если на участке действия распределенной нагрузки эпюра пересекает базовую линию, то в этом сечении изгибающий момент принимает экстремальное значение.
- Если на границе распределенной нагрузки не приложено сосредоточенных сил, то на эпюре Q участок, параллельный оси абсцисс, переходит в наклонный без скачка, а параболическая и наклонная части эпюры Ми сопрягаются плавно без изгиба.
-Изгибающий момент в концевых сечениях балки всегда равен нулю
(точка А), за исключением случая, когда в концевом сечении действует сосредоточенная пара сил. В этом случае изгибающий момент в концевом сечении балки равен моменту действующей пары сил.
- В сечении, соответствующем заделке, Q и Ми численно равны опорной реакции и реактивному моменту (точка D).
3 Подбираем номер профиля двутавра из условия прочности при изгибе, если [σ]и = 160 МПа.
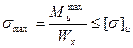
Отсюда
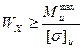
где Wx - осевой момент сопротивления сечения;
М - максимально изгибающий момент, т.е. наибольший по абсолютной величине, определяем непосредственно из эпюры Ми.
Тогда
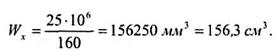
По значению Wx = 156,3 см3 (приложение Б сортамента) подходит двутавровый профиль № 20, для которого Wx = 184 см3.
Для балок, имеющих много участков нагружения, т.е. нагруженных комбинацией нагрузок, целесообразно строить эпюры по характерным сечениям, а именно: вычислять поперечные силы и изгибающие моменты только для сечений, в которых эпюры претерпевают изменения, а затем, зная закон изменения эпюры между найденными сечениями, соединить их соответствующими линиями. К характерным относятся сечения, в которых приложены сосредоточенные силы или моменты, а также сечения, где начинается или кончается распределенная нагрузка.
Для того чтобы вычислить поперечную силу и изгибающий момент в произвольном сечении, необходимо рассечь плоскостью в этом месте балку и часть балки (любую), лежащую по одну сторону от рассматриваемого сечения, отбросить. Затем по действующим на оставленную часть балки внешним силам надо найти искомые значения Qy и Мх, причем знак их надо определить по тому действию, какое оказывают внешние силы на оставленную часть балки в соответствии с принятым ранее правилом знаков.
При построении эпюры слева направо отбрасывается правая часть балки, a Qy и Мх находятся по силам, действующим на левую часть. При построении эпюры справа налево, наоборот, отбрасывается левая часть, a Qy и Мх определяются по силам, действующим на правую часть балки.
Пример 19
Для балки, показанной на рисунке 30 построить эпюры поперечных сил и изгибающих моментов. Подобрать сечение в виде сдвоенного швеллера, если [σ]и =130 МПа.
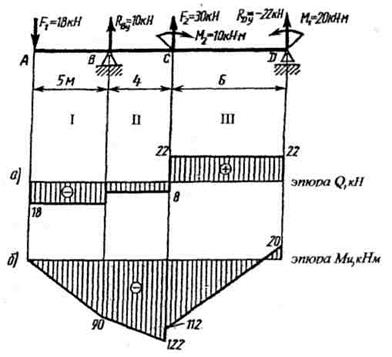
Рисунок 30
Решение
1 Прежде, чем приступить к построению эпюр Q и Ми необходимо определить реакции опор:
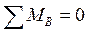
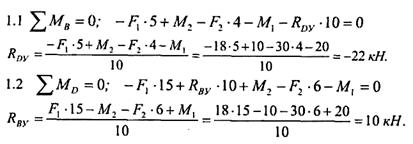
|
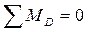
Для проверки составляем алгебраическую сумму проекций всех сил на ось У:
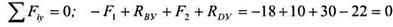
2 Определяем поперечную силу на каждом участке и строим эпюру (рисунок 30а).

В выбранном масштабе на рисунке 30а откладываем найденные значения поперечной силы. Эпюра построена.
Определяем значения изгибающих моментов в сечениях А, В, С, D:

т.к. в концевом сечении приложен внешний сосредоточенный момент.
В сечении А момент равен нулю, т.к. в концевом сечении не приложен внешний сосредоточенный момент.
В выбранном масштабе на рисунке 30 б строим эпюру изгибающих моментов.
В сечении С на эпюре наблюдается скачок, равный М2 = 10 кНм.
3 Определяем номер швеллера из условия прочности. Опасным будет сечение С, где возникает максимальный изгибающий момент
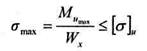
для 2-х швеллеров:

|
для 1-го швеллера: 
По таблице сортамента (приложение В) подбираем швеллер №33,
для которого WX = 484,0 см3.
Пример 20
|
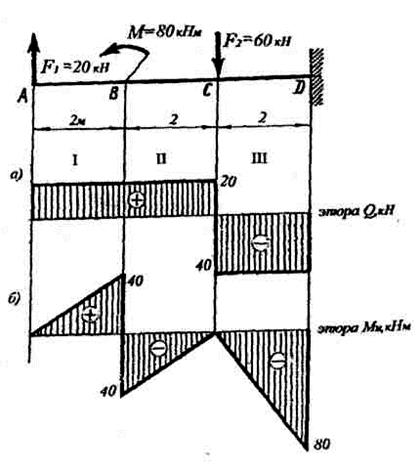
Для консольной балки, изображенной на рисунке 31, построить эпюры поперечных сил и изгибающих моментов. Подобрать номер двутавра, если [σ]и = 160 МПа.
Рисунок 31
Решение
С левой стороны на балку не наложено никаких связей и поэтому эпюры строим со свободного левого конца балки.
1 Определяем поперечную силу Q на каждом участке:
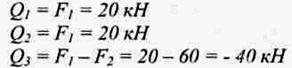
Выбираем масштаб и строим эпюру на рисунке 31а.
2 Определяем изгибающий момент в каждом сечении:
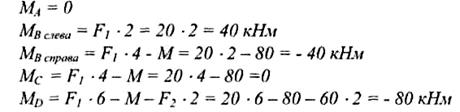
Выбираем масштаб и строим эпюру по найденным значениям изгибающих моментов на рисунке 31 б.
3 Определяем номер двутавра из условия прочности:

Тогда
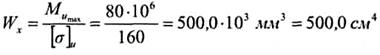
По таблице сортамента (приложение Б) подбираем двутавр № 36, для которого Wx = 516,0 см3.
Раздел «Детали машин»
Раздел "Детали машин" является не только завершающим в изучении предмета "Техническая механика", но, синтезируя в себе достижения дисциплин физики, математики, материаловедения, черчения и первых двух разделов технической механики, является связующим звеном между общетехническими и специальными дисциплинами. При изучении раздела "Детали машин" студенты приобретают навыки основ расчета, проектирования и конструирования деталей машин общего назначения. При изучении раздела и особенно в процессе выполнения контрольной работы студенты должны научиться делать обобщения и анализ получаемых результатов, приобрести умение оценивать их физическую правдоподобность, получить навыки самостоятельной работы с технической и справочной литературой. Принятые конструктивные решения по проектируемым изделиям нужно оценивать не только по прочности, но и по технологическим, а также экономическим критериям.
Изучение каждой детали или сборочной единицы целесообразно вести в такой последовательности:
назначение, устройство, принцип работы; достоинства, недостатки, область применения; краткие сведения о материалах и конструктивных формах;
основы расчета (геометрический расчет, действующие силы, расчеты на прочность, долговечность, износостойкость и др.);
основные сведения о конструкции. Усвоив основные определения, классификацию машин и тенденции развития отечественного машиностроения, следует особое внимание уделить изучению вопросов стандартизации и системы документации: конструкторской (ЕСКД), технологической (ЕСТД) и допусков (ЕСДП), их роли в общем процессе ма-шино- и приборостроения, а также в процессе их ремонта и обслуживания.
Изучая вопросы критериев работоспособности и расчета деталей машин, следует уяснить, что эти расчеты имеют ряд особенностей. В частности, широко используются эмпирические зависимости и формулы, являющиеся результатом обобщения опыта проектирования и расчета деталей машин.
Проектирование требует всестороннего анализа поставленной задачи, учета ряда специфических факторов и условий работы детали, узла, машины. Рационально спроектированная машина должна быть прочной, долговечной, возможно дешевой и экономичной в работе, должна быть безопасной при обслуживании. Окончательные размеры деталей машины определяются не только расчетами, но и требованиями стандартов, принятой технологией производства, условиями эксплуатации и технической безопасности.
Задачи №№ 21-30
К решению этих задач следует приступить после изучения темы 3.2 "Соединение деталей", "Разъемные и неразъемные соединения" и внимательного изучения примера 21.
При изучении неразъемных соединений, среди которых наибольшее распространение получили сварные, необходимо восстановить в памяти физическую суть сварки и ее разновидности. Ознакомиться с типами сварных швов и способами подготовки кромок соединяемых деталей в зависимости от их толщины. Уяснить достоинства и недостатки сварных соединений, и их преимущества по сравнению с заклепочными. Повторить методику расчетов на смятие и срез, ознакомиться с выбором допускаемых напряжений и методикой практических расчетов основных типов сварных соединений.
Одним из наиболее распространенных видов разъемных соединений, применяемых во всех областях машиностроения, являются резьбовые соединения. При изучении их нужно внимательно рассмотреть типы и назначение резьб и крепежных деталей, средства стопорения (гаечные замки). Изучая резьбовые соединения, необходимо уяснить, что в большинстве случаев расчет болтов (винтов) сводится к расчету на растяжение с учетом соответствующих поправочных коэффициентов.
Разъемные соединения могут осуществляться штифтами.
Цилиндрические штифты применяют как установочные или для передачи небольших нагрузок.
При передаче поперечной нагрузки штифт работает на срез и смятие.
Пример 21
Соединение деталей 1 и 2, изображенное на рисунке 34, нагружено силой F = 70 кН и осуществлено через накладку 2. Накладка приварена к детали 1 фланговыми швами, а к детали 3 -шарнирным соединением с помощью штифта. Определить длину ℓф каждого сварного шва и диаметр штифта d. Для материала штифта принять [τ]ср = 80 Н/мм2, для материала сварного шва [τ]ср ' = 100 H/ мм2. Расчет шарнирного соединения на смятие производить не требуется, так как принято пониженное значение [τ]ср.
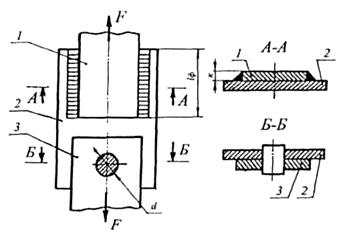
Рисунок 34
Решение
1 Из условия прочности сварных швов при срезе определяем длину ℓф
каждого шва, учтя, что суммарная длина швов ℓ = 2.ℓф, и приняв катет шва
к = 5 мм (рисунок 34):
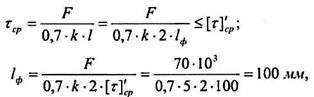
2. Из условия прочности пальца при срезе определяем его диаметр d:
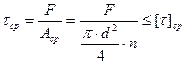 ,
,
где n - число плоскостей среза. По рисунку 34 n = 1

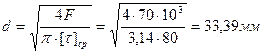
Принимаем по ряду Rа40 диаметр d = 34 мм (приложение А)
Задачи №№ 31-40
К решению этих задач следует приступить после повторения относящегося к вращательному движению материала разделов "Кинематика" и "Динамика", изучения темы 3.3 "Передачи вращательного движения", уяснения приведенных ниже методических указаний и разбора примера 22.
Вращательное движение наиболее распространено в технике. Поэтому для передачи от машин-двигателей к исполнительным механизмам применяют механические передачи, главным образом вращательного движения.
Механические передачи классифицируют по принципу действия (передачи трением и зацеплением) и взаимному расположению звеньев (передачи непосредственного контакта и передачи гибкой связью). Независимо от типа передачи общим для всех является наличие ведущих и ведомых звеньев, единство кинематических и силовых соотношений.
В предлагаемых задачах требуется определить кинематические (ω) и силовые (Р, М) параметры для всех валов многоступенчатой передачи привода. Приступая к решению задачи, следует ознакомиться с ГОСТами на условные обозначения элементов и с правилами выполнения кинематических схем. Валы и звенья нумеруются по направлению силового потока (направлению передачи движения) - от ведущего вала (вал двигателя) к ведомому валу. Индекс в обозначениях параметров валов ω, Р и М соответствует номеру вала, а в обозначениях d и z - номеру насаженного на вал звена (колеса, шкива, звездочки и т.п.). Параметры любого последующего вала определяют через заданные параметры ведущего вала при условии, что известны КПД и передаточные отношения отдельных передач привода. Напоминаем, что при последовательном соединении общее передаточное отношение равно произведению передаточных отношений отдельных передач, то же - для КПД.
Следует помнить, что для зубчатых, червячных и цепных передач передаточное число равно:
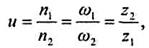
|
для ременных и фрикционных:
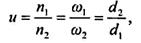
где индекс 1 относится к ведущему, а индекс 2 - к ведомому звену передачи.
Приводим таблицу 16 средних значений КПД некоторых передач
(с учетом потерь в подшипниках):
Таблица 16
| Тип передачи | Закрытая | Открытая |
| Зубчатая цилиндрическая | 0,98 | 0,96 |
| Зубчатая коническая | 0,97 | 0,95 |
| Червячная | 0,8 | - |
| Цепная | - | 0,92 |
| Клиноременная | - | 0,95 |
Пример 22
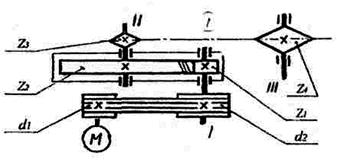
Привод состоит из электродвигателя мощностью Рдв= 11 кВт с частотой вращения вала пдв= 1460 об/мин и многоступенчатой передачи. Требуется определить: общие КПД и передаточное число привода; мощности, вращающие моменты и угловые скорости для всех валов, если иред = 4, d1 = 80 мм, d2 =200 мм, z3 = 25, z4 = 75 (рисунок 35).
|
Рисунок 35
Решение
1 Кинематическая и конструктивная характеристики привода: передача трехступенчатая, понижающая (т.е. уменьшающая угловую скорость, так как в каждой ступени диаметр выходного звена больше, чем входного). Первая ступень - передача клиноременная, вторая - редуктор цилиндрический косозубый, т.е. передача понижающая в герметичном корпусе, третья ступень - передача цепная.
2 КПД передач:
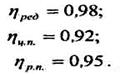
|
косозубого редуктора:
цепной передачи:
клиноремённой передачи:
Общий КПД передачи равен:
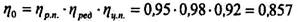
|
3 Мощности валов:
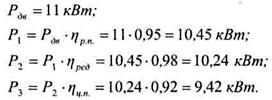
Мощность на третьем валу можно определить и иначе:

4 Передаточные числа отдельных передач:
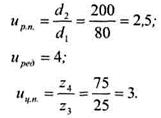
Общее передаточное число равно:
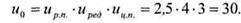
5 Угловые скорости всех валов:
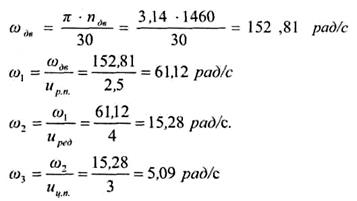
Угловую скорость третьего вала (выходного) можно было определить иначе:

Отсюда
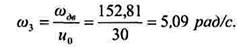
6 Вращающие моменты на валах:

В понижающих передачах понижение угловых скоростей валов сопровождается соответствующим повышением вращающих моментов.
Мощности на валах снижаются незначительно вследствие потерь на трение в подшипниках и при взаимодействии звеньев.
Задачи №№41-50
К этим задачам следует приступить после изучения темы 3.3 "Передачи вращательного движения", уяснения методических указаний к теме и разбора примеров 23, 24.
Необходимо усвоить классификацию зубчатых передач по расположению геометрических осей в пространстве, по окружной скорости и по конструктивным признакам (закрытие и открытие передачи). Следует достичь полного понимания основной теоремы зацепления, поскольку она определяет профилирование зубьев. Из множества профилей, удовлетворяющих требованиям основной теоремы зацепления, практическое применение получил эвольвентный.
Изучая зацепление пары эвольвентных зубчатых колес, необходимо запомнить определение основных элементов и характеристик зацепления по ГОТу (делительные окружности, полюс зацепления, головка и ножка зуба, окружности выступов и впадин, шаг зацепления, линия зацепления, угол зацепления, основная окружность, основной шаг, длина зацепления (рисунок 36)). Рассматривая зацепление эвольвентного зубчатого колеса с рейкой, отметьте на последней начальную прямую, которая перекатывается без скольжения по начальной окружности колеса. На примере зацепления колеса с рейкой уясните принципиальные основы нарезания зубчатых колес методом обкатки и запомните определение делительной окружности зубчатого колеса. Рассматривая исходный контур зубчатой рейки по СТ СЭВ 308-76 для цилиндрических и по СТ СЭВ 309-76 для конических колес, обратите внимание на стандартные параметры нормального зубчатого зацепления. Изучите виды повреждения зубьев и уясните основные критерии их работоспособности и расчета.
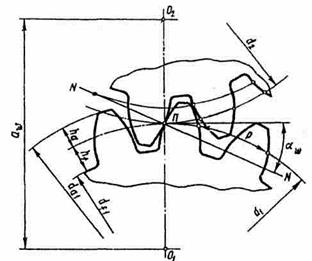
Рисунок 36
Расчет закрытых зубчатых передач на контактную усталость ведется по нормальным контактным напряжениям. Контактная усталость зубьев определяется межосевым расстоянием или диаметрами колес. При расчете на изгиб обратите внимание на коэффициент формы зуба, его зависимость от числа зубьев и в связи с этим на различную прочность зубьев шестерни и колеса.
При изучении косозубых и шевронных цилиндрических передач сопоставьте их расчеты на прочность с расчетами прямозубых цилиндрических передач и выявите особенности соответствующего расчета. Можно заметить, что непрямозубые колеса имеют большую несущую способность, чем прямозубые, как по контактной усталости, так и по изгибу. Все расчеты непрямозубых цилиндрических и прямозубых конических передач следует связать с эквивалентными колесами: для цилиндрических передач - в сечении, перпендикулярном оси зуба, для конических - на развертке так называемых дополнительных конусов.
Все расчеты следует выполнять с точностью до сотых долей миллиметра, значение косинуса и синуса угла наклона линии зуба следует вычислять с точностью до шести знаков.
При изучении темы 3.3 необходимо разобраться в устройстве червячной передачи, ее достоинствах, выяснить ее недостатки и области применения. Следует обратить внимание на конструкцию червяков и червячных колес. Размеры червячного колеса определяются в среднем сечении. Необходимо усвоить методику выбора числа витков червяка zt и числа зубьев колеса z 2, связав их с передаточным числом червячной передачи. Следует уяснить, что с увеличением числа витков червяка одновременно увеличивается и износ рабочих элементов передачи, поэтому не рекомендуется применять червяки с числом витков более четырех. Работоспособность червячной передачи зависит не только от прочности зубьев червячного колеса, но и от прочности и жесткости червяка, а также от качества смазки, которая по праву рассматривается как составная часть конструкции. С целью обеспечения работоспособности передачи следует выполнять тепловой расчет.
В предлагаемых задачах требуется выполнить геометрический расчет (определить основные геометрические размеры) зубчатой цилиндрической или червячной передачи. Этот расчет, кaк известно, базируется на заданном межосевом расстоянии аw. При расчете студенты должны применять наименования и обозначения расчетных параметров только в соответствии с действующими ГОСТами.
Методика геометрического расчета зубчатых цилиндрических передач. Исходные данные: передаточное число иред, межосевое расстояние аw коэффициент ширины венца колеса ψва, вращающий момент на ведомом валу Т2.
1 Выбираем нормальный модуль по эмпирическому соотношению:
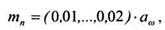
принимая стандартное значение модуля по ряду Ra40: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20.
2 Определяем b2 ширину венца колеса
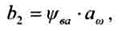
ψва - коэффициент ширины венца колеса. При симметричном расположении шестерни относительно опор принимаем
ψва=0,4.
3 Предварительно определяем минимальный угол наклона зубьев:

Точность вычислений - до шестого знака после запятой.
Должно выполняться условие: βmjn > 80.
Для прямозубых передач β = 0.
4 Определяем суммарное число зубьев
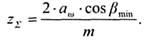
Округляем полученное значение до ближайшего целого числа.
5 Уточняем угол наклона зубьев:
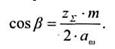
6 Определяем число зубьев шестерни и колеса:
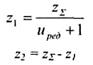
7 Уточняем передаточное число

8 Определяем основные геометрические параметры:
8.1 Шаг зацепления р = π . т;
8.2 Высота головки зуба ha = m;
8.3 Высота ножки зуба hf = 1,25 . т
9 Определяем фактические основные геометрические размеры передачи:
9.1 Делительные диаметры шестерни и колеса:

9.2 Диаметры вершин шестерни и колеса:

9.3 Диаметры впадин шестерни и колеса

9.4 Межосевое расстояние

10 Определяем силы в зацеплении, рисунок 37.
10.1 Окружная сила
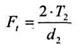
10.2 Радиальная сила

где αw = 20° - угол зацепления.
10.3 Осевая сила
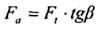
Пример 23
Выполнить геометрический расчет цилиндрической косозубой передачи редуктора, аw= 100 мм, иред = 4, Т2 = 200 Нм.
Решение
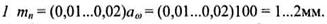
Выбираем стандартное значение m = 2 мм.
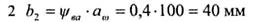
ψеа - коэффициент ширины венца колеса. При симметричном расположении шестерни относительно опор принимаем \|/ва = 0,4.

Полученное значение zΣ округляют в меньшую сторону.
Принимаем zΣ= 97.
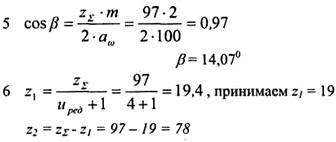
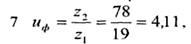
Что больше заданного на 2,6% (допускается отличие до 5%).
8 Определяем основные геометрические параметры зацепления

9 Фактические основные геометрические параметры 
10 Определяем силы в зацеплении, рисунок 37:


Рисунок 37
Пример 24
Выполнить геометрический расчет цилиндрической прямозубой передачи редуктора, аw = 140 мм, иред = 5, Т2 = 292 Нм.
Решение
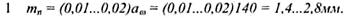
Выбираем стандартное значение m = 2 мм.

6 Определяем фактические основные геометрические парaметры передачи:
6.1 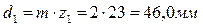

6.2 
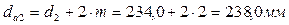
6.3 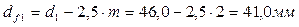
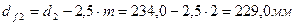
6.4 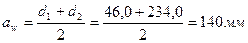

|
7 Определяем силы в зацеплении, рисунок 38:
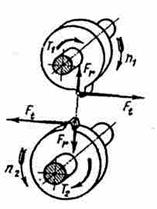
Рисунок 38
Методика геометрического расчета червячных передач.
Исходные данные: передаточное число иред, межосевое расстояние аw,
вращающий момент Т2.
1 Выбираем число заходов червяка z1 из таблицы 17 в зависимости от иред.
Таблица 17
| upeд | 8...14 | св. 14...30 | св.30 |
z1 
|
2 Определяем число зубьев червячного колеса:
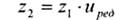
|
3 Определяем модуль зацепления:

Выбираем стандартное значение модуля 2,0; 2,5; 3,15; 4; 5; 6,3; 8; 10,0; 12,5; 16; 20; 25
4 Определяем коэффициент диаметра червяка:
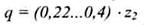
Выбираем стандартное значение коэффициента диаметра червяка: 6,3; 8,0; 10; 12,5; 16; 20; 25.
5 Определяем основные геометрические параметры зацепления:
5.1 осевой шаг червяка и окружной шаг колеса;
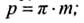
5.2 высота головки витка червяка и зуба колеса;
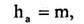
5.3 высота ножки витка червяка и зуба колеса;
hf = 1,2. m
6 Определим основные геометрические размеры червяка:
6.1 делительный диаметр d1 = m . q;
6.2 диаметр вершин витков da1= d1+ 2 . ha;
6.3 диаметр впадин df1 = d1 – 2. hf;
6.4 делительный угол подъема линии витка tg ψ = 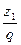 ;
;
6.5 длина нарезанной части червяка b1
b1 = m . (11+ 0,06 . z2)
7 Определяем основные геометрические размеры венца червячного колеса
7.1 делительный диаметр d2 = m . z2
7.2 диаметр вершин зубьев da2 = d2 + 2 . ha
7.3 диаметр впадин зубьев df2 = d2 – 2 . hf
7.4 наружный диаметр колеса 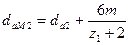 ;
;
7.5 ширину венца червячного колеса определяем по формуле в зависимости от числа витков червяка по таблице 18
Таблица 18
| Число заходов червяка | Ширина венца червячного колеса |
| При z1 = 1 | b2 = 0,355 . aw |
| z1 = 4 | b2 = 0,315 . aw |
8 Определяем силы в червячном зацеплении (рисунок 39).
8.1 Окружная сила на колесе и осевая сила на червяке:
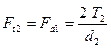
8.2 Окружная сила на червяке и осевая сила на колесе:
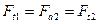
8.3 Радиальная сила на червяке и на колесе:
 ,
,
где α = tg200 – угол профиля витка
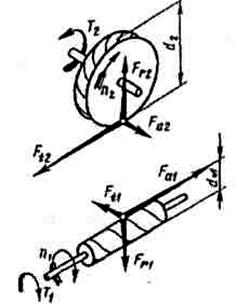
Рисунок 39
Пример 25
Выполнить геометрический расчет червячной передачи редуктора. Исходные данные: межосевое расстояние аw = 250 мм; передаточное число редуктора иред = 30; вращающий момент на валу червячного колеса Т2 = 380 Нм, коэффициент полезного действия ηред = 0,8.
Решение
1 Из таблицы 17 выбираем z1 = 2
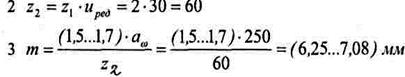
Принимаем стандартное значение т = 6,3 мм.
Принимаем стандартное значение q = 16.
5 Определяем основные геометрические параметры зацепления:
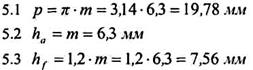
6 Определяем основные геометрические параметры червяка:
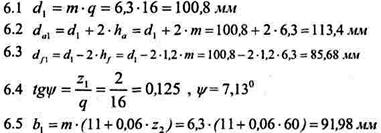
Принимаем по ряду Ra40 b1 = 95 мм.
7 Определяем основные геометрические размеры венца червячного колеса:
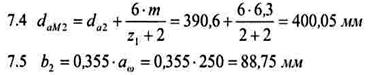
|
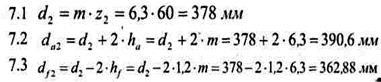
По ряду Ra40 (приложение А) выбираем b2 = 90 мм.
8 Определяем силы в червячном зацеплении (рисунок 39):

Не нашли, что искали? Воспользуйтесь поиском: