
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Погрешности приборов
p = 0.95
| Прибор | Цена наименьшего деления, ω | Предельная погрешность прибора, δ | Погрешность округления, D окр | Погрешность прибора, D пр |
| Микрометр | 0.01 мм | 0.01 мм | 0.005 мм | 0.007 мм |
| Штангенциркуль | 0.1 мм | 0.1 мм | 0.05 мм | 0.07 мм |
| Штангенциркуль | 0.05 мм | 0.05 мм | 0.02 мм | 0.03 мм |
| Весы технические | 0.1 г (100 мг) | 0.01 г | 0.05 г | 0.07 г |
| Линейка | 1 мм | 1 мм | 0.5 мм | 0.7 мм |
| Секундомер | 0.2 с | 0.2 с | 0.1 с | 0.14 с |
8. Определяем суммарную абсолютную погрешность D x опыта по формуле
 . .
| (1.1.6) / (7.5.1) |
При вычислении D x по формуле (1.1.6) можно отбросить одну или две из погрешностей 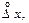 D пр и ∆ окр, если их величины вдвое или значительно меньше оставшихся.
D пр и ∆ окр, если их величины вдвое или значительно меньше оставшихся.
9. Округляем абсолютную погрешность D x (см. параграф 9.1):
· до одной значащей цифры, если эта цифра больше или равна 2. Например,
Dx = 0. 523  0. 5;
0. 5;
· до двух значащих цифр, если первая из них меньше 2. Например,
D x = 0. 124  0. 12.
0. 12.
Здесь и в ряде следующих примеров значащие цифры подчеркнуты.
10. Записываем окончательный результат эксперимента в виде
| X = < х > ± D x | (p = 0.95) | (1.1.7) / (5.1.1) |
и указываем единицы измерения.
Запись (1.1.7) означает, что истинное значение X измеряемой величины x лежит в доверительном интервале (<x> - D x, < x > + D x) с вероятностью p, составляющей 95 %.
11. Округляем среднее значение < x > таким образом, чтобы погрешность D x приходилась (см. параграф 9.1):
· на последний разряд среднего < x >, если D x записано с одной значащей цифрой
X = (6438 ± 523)  (6.4 ± 0. 5)∙103 м (6.4 ± 0. 5)∙103 м
| (p = 0.95); | (1.1.8) |
· на два последних разряда среднего < x >, если D x записано с двумя значащими цифрами
X = (6438 ± 124)  (6.44 ± 0. 12)∙103 м (6.44 ± 0. 12)∙103 м
| (p = 0.95). | (1.1.9) |
12. Определяем относительную погрешность D xотн результата серии измерений
| D xотн = D x/ < x >. | (1.1.10) / (6.2.1) |
13. Записываем теоретическое, или табличное, или полученное в других исследованиях и т.д., значение изучаемой нами физической величины x. Приводим подробную ссылку на цитируемый источник.
Например: Табличное значение плотности алюминия при температуре 20° С
ρ = 2.69 г/см3.
См.: Таблицы физических величин: Справочник / Под ред. И.К. Кикоина. М.: Атомиздат. 1976. 1006 с. (таблица на с. 121).
14. Сравниваем полученный в наших экспериментах результат с данными предыдущего пункта 13. Если эти результаты значительно различаются, следует установить причины такого расхождения: проверить вычисления; повторить измерения для одного - двух характерных значений параметров.
15. Записываем вывод.
Например: В пределах погрешности эксперимента результаты наших измерений согласуются (не согласуются) с теоретическим, или табличным, или приведенным в цитируемой работе [N] значением. (Расхождение результатов может быть обусловлено следующими причинами: …, или следующими недостатками используемых приборов и методики эксперимента: …).
1.2. Обработка результатов косвенных измерений
Косвенными называются измерения, при которых интересующая нас величина z является функцией k (k  1) непосредственно измеряемых величин x1, x2,…, xk:
1) непосредственно измеряемых величин x1, x2,…, xk:
| z = z (x1, x2,…, xk). | (1.2.1)/(8.4.1) |
При обработке результатов косвенных измерений наиболее распространен следующий способ.
1. Данные прямых измерений каждого из параметров x1, x2,…, xk обрабатываем, как описано в параграфе 1.1:
· Вычисляем средние арифметические значения аргументов <x1>, <x2>, …, <xk> по формуле (1.1.1);
· Находим абсолютные погрешности D x1, D x2, …, D xk измерений каждого из аргументов, пользуясь приведенными выше формулами (1.1.3) – (1.1.6). При этом для всех аргументов задаем одно и то же значение надежности p = 0.95.
2. Результат косвенного измерения определяем, подставляя найденные средние <x1>, <x2>, …, <xk> от непосредственно измеренных величин в формулу для функции z
| z = z (<x1 >, <x2 >, …, <xk >). | (1.2.2)/ (8.4.5) |
3. Абсолютную погрешность D z для результата косвенных измерений оцениваем по формуле

| (1.2.3)/ (8.4.6) |
где  - частные производные[6] функции z, вычисляемые при значениях переменных x1 = <x1>, x2 = <x2>, …, xk = <xk>.
- частные производные[6] функции z, вычисляемые при значениях переменных x1 = <x1>, x2 = <x2>, …, xk = <xk>.
Результирующая погрешность D z имеет ту же надежность p = 0.95.
При вычислении результирующей погрешности по формуле (1.2.3) следует пренебречь теми из слагаемых в подкоренном выражении, которые по крайней мере вдвое меньше оставшихся членов.
Еще один способ обработки результатов косвенных измерений описан далее в параграфе 8.4.
2. ОФОРМЛЕНИЕ ОТЧЕТОВ О ЛАБОРАТОРНЫХ РАБОТАХ [7]
1. Каждая работа должна начинаться с новой страницы.
2. Заголовок работы должен быть выделен.
3. После заголовка необходимо записать краткое Введение, в котором должны быть отражены следующие моменты:
· постановка задачи, какое явление или какая зависимость будут исследованы, что ожидается получить в ходе выполнения работы;
· физические величины, которые будут измеряться в работе; каковы их размерности и единицы измерения;
· описание метода измерений, используемого в работе. При этом обязательно следует схематически нарисовать экспериментальную установку и написать рабочую формулу и формулы для вычисления погрешностей.
4. Экспериментальные результаты следует записывать только в рабочую тетрадь, в заранее заготовленные таблицы. Не следует использовать для этих целей черновики.
5. Если измеряемая величина зависит от внешних условий, например, от температуры или давления, необходимо записать условия эксперимента.
6. Окончательный результат следует записать в конце отчета с указанием доверительного интервала, коэффициента надежности, единиц измерения и внешних условий. Этот результат должен быть выделен.
7. Если возможно, полученный результат необходимо сравнить с имеющимися табличными данными, теоретическими расчетами или результатами экспериментов других авторов, обязательно приведя при этом ссылку на источник этих данных.
8. Если в измерениях содержатся систематические погрешности (например, сила трения, не учтенная в формулах), то указывать доверительный интервал не имеет смысла [4, 5]. В этом случае ограничиваются оценкой точности метода измерений.
9. Для характеристики качества результатов и используемого экспериментального метода рекомендуется всегда оценивать относительную погрешность результата.
10. Все записи в тетради должны быть датированы.
ВВЕДЕНИЕ
Основными задачами лабораторной практики являются:
· знакомство с приборами;
· приобретение опыта в проведении эксперимента;
· иллюстрация теоретических положений физики.
Очевидно, что ни один курс практических работ не сможет включить в себя всю теорию и познакомить со всеми приборами. Поэтому главная задача настоящего практикума - научиться:
· планировать эксперимент так, чтобы точность измерений соответствовала поставленным целям;
· учитывать возможность систематических ошибок и принимать меры для их устранения;
· анализировать результаты эксперимента и делать правильные выводы;
· оценивать точность окончательного результата;
· вести записи измерений и расчетов аккуратно, ясно и кратко.
Познакомиться с приемами практического проведения измерений, статистической обработки их результатов, с методами экспериментальных исследований и указаниями по оформлению результатов, составлению отчетов и написанию научных статей мы рекомендуем по книге Дж. Сквайрса «Практическая физика» [4].
Предлагаемый лабораторный практикум по механике как одному из разделов физики призван не столько сообщить читателю новые сведения – это уже выполнено школой – сколько помочь ему глубже понять существо более или менее известных фактов и их взаимосвязь. Эта основная наша цель непосредственно связана также с воспитанием творческих способностей и формированием самостоятельного мышления. Такое воспитание может формироваться на следующих основных направлениях: умение обобщать – индукция; умение применять теорию к конкретной задаче – дедукция и, пожалуй, самое важное – умение выявлять противоречия между теоретическими обобщениями и практикой – диалектика.
В теоретической картине, которая Вам преподносится на лекциях, рассматриваются те стороны реального мира, которые теория считает важными. Может получиться так, что Ваше знакомство с миром природы ограничится только этими сторонами, и Вы будете уверены, что это и есть весь реальный мир, а не отдельные его грани. К тому же в такой картине все так хорошо увязано, что легко утратить представление о том, какие усилия потребовались для ее создания. Лучшее лекарство от такой болезни – пойти в лабораторию и там убедиться в сложности реального мира.
Занимаясь экспериментальной физикой, Вы прежде всего узнаете, как трудно бывает проверить теорию, измерить то, что нужно, а не что-то иное, и научитесь преодолевать такие трудности. Вместе с тем, у Вас появится взгляд на физику в целом и на взаимоотношения между теорией и экспериментом.
Чтобы научить оформлению отчетов о научном исследовании (для Вас это обучение разбивается на этапы – лабораторные работы, студенческие научные семинары и конференции, участие в исследованиях кафедры), часть приводимых далее описаний лабораторных работ составлена в стиле статей в научных журналах. О том, как писать научные статьи, подробно говорится в книгах [4], [6], где даются практические советы, рекомендации и приводятся образцы. Мы здесь укажем только, что в таких описаниях будем придерживаться общепринятого разбиения статьи на следующие разделы:
· введение с постановкой задачи;
· описание экспериментальной установки и методики измерений;
· результаты эксперимента;
· их анализ и сопоставление с результатами других авторов;
· выводы.
Для всех физиков мира подобная манера изложения стала настолько неотъемлемым профессиональным навыком, что часто служит поводом для шуток и пародий – смотри, например, статьи П. Иордана и Р. де Кронига «Движение нижней челюсти у крупного рогатого скота в процессе пережевывания пищи» и Я. И. Френкеля «К квантовой теории танца» в книге [6]. Не удержались от подобной шутки над штампами и над собой и авторы данного издания, поместив в разделе «Обсуждение результатов» совместной публикации [7] в уважаемом академическом журнале дословную цитату из пародии «Инструкция для читателя научных статей» [6]: «Если принять во внимание приближения, сделанные при анализе, согласие экспериментальных и теоретических результатов следует признать удовлетворительным», но, правда, опустив раскрытый в «Инструкции…» тайный смысл этой фразы: «Согласие вообще отсутствует» - в уверенности, что посвященные поймут этот смысл и без дополнительных разъяснений.
Для того чтобы продемонстрировать, насколько полезно, сообщая экспериментальные данные, указывать не только средние характеристики, но и доверительные интервалы, в пределах которых наиболее вероятно нахождение истинных значений измеряемых величин, а также показать, как могут соотноситься теоретические и экспериментальные результаты при изучении конкретных задач, приведем два графика из упомянутой статьи [7].
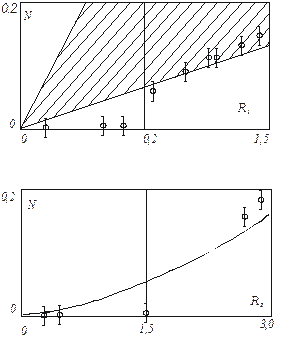
| Фигура 1 из работы [7]. Тепловой поток через пропитанную жидкостью пористую среду с мелкими порами. Точки - данные опытов. Область теоретических значений заштрихована Фигура 2 из работы [7]. Теплоперенос через среду с крупными порами. Точки – эксперимент; кривая – теория |
4. ВИДЫ ИЗМЕРЕНИЙ
Измерение
Измерением какой-либо физической величины называется операция, позволяющая узнать, во сколько раз измеряемая величина больше (или меньше) соответствующей величины, принятой за единицу.
Необходимо подчеркнуть, что такое сравнение с эталоном – измерение – должно выполняться в строго определенных условиях и вполне определенным образом. Например, измерение длины предмета предполагает, что эталон неподвижен по отношению к нему, а измерение продолжительности события производится по неподвижным часам. В этом смысле поучителен разбор Эйнштейном понятия одновременности, которое в классической физике не определялось вообще как a priori «очевидное».
Измерения разделяются на прямые и косвенные.
Прямые измерения
Прямыми называются такие измерения, при которых искомая величина сравнивается с единицей измерения непосредственно или при помощи измерительного прибора, проградуированного в соответствующих единицах. Примерами прямых измерений являются измерения длины линейкой или штангенциркулем; измерения масс на рычажных весах с помощью набора разновесов; измерения промежутков времени при помощи часов или секундомера, измерения температуры термометром, напряжения вольтметром и т.п. Значение измеряемой величины отсчитывается при этом по шкале прибора или определяется подсчетом мер, разновесов и т.д.
Не нашли, что искали? Воспользуйтесь поиском: