Черт. 86. К примеру расчета 53

Расчет. h_o = h ¾ а = 400 ¾ 58 = 342 мм. Так как то, согласно п. 4.1, принимаем, что элемент работает с трещинами в растянутой зоне.

Для определения продолжительного раскрытия трещин вычислим напряжение в арматуре s _s. Согласно формуле (263), величина s _s на уровне центра тяжести арматуры равна:

Поскольку арматура расположена в два ряда, вычислим по формуле (262) коэффициент d _n:

Напряжение в нижнем стержне арматуры равно:

s _s = 273 ×1,08 = 294МПа.

Ширину раскрытия трещин находим по формуле (249). Так как 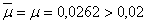, значение принимаем равным 0,02. Согласно п. 4.7, d = 1,0; h = 1,0; d = 22 мм.

что меньше предельно допустимой ширины раскрытия трещин a_crc2 = 0,3 мм.

Пример 54. Дано: железобетонная плита фундамента с размерами поперечного сечения h = 300 мм, b = 1150 мм; a = 42 мм; бетон тяжелый класса В15 (_Rbt,ser = 1,15 МПа; E_b = 2,05 ×10 ⁴ МПа); рабочая арматура класса A-III (R_s = 365 МПа; Е _s = 2 ×10 ⁵ МПа); площадь ее сечения А _s = 923 мм ² (6 Æ14); момент в расчетном сечении от постоянных и длительных нагрузок M_l = 63 кН ×м, от кратковременных нагрузок M_sh = 4 кН ×м; предельный момент по прочности М _u = 80,5 кН ×м; фундамент расположен выше уровня грунтовых вод.

Требуется произвести расчет по раскрытию нормальных трещин.

Расчет. h_o = h ‑ а = 300 ‑ 42 = 258 мм. Определим необходимость вычисления ширины раскрытия трещин согласно п. 4.5. Для этого найдем момент трещинообразования M_crc.

Так как момент M_crc находим как для бетонного сечения, используя формулу (246):

M_crc = R_bt,serW_pl = 0,292 bh²R_bt,ser = 0,292 ×1150 ×300 ² ×1,15 = 34,75 ×10 ⁶ Н ×мм = 34,8 кН ×м.

Так как M_r = М _tot = M_l + М _sh = 63 + 4 = 67 кН ×м > M_crc = 34,8 кН ×м, проверка ширины раскрытия трещин необходима.

Поскольку фундамент расположен выше уровня грунтовых вод, допустимая ширина продолжительного раскрытия трещин, согласно табл. 1, поз. 4, a_crc2 = 0,3 мм, поэтому при 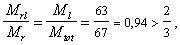согласно п. 4.6, расчет производим только на продолжительное раскрытие трещин от действия момента M_l.

Ширину раскрытия трещин определим по формуле (249).

Напряжение в арматуре s _s вычислим по упрощенной формуле (263):

Коэффициенты, вводимые в формулу (249), принимаем равными: d = 1,0; h = 1,0; d = 14 мм, тогда

что больше допустимого значения a_crc2 = 0,3 мм, в связи с чем целесообразно произвести корректировку значения a_crc в меньшую сторону согласно п. 4.8б. Поскольку такая корректировка допускается. Так как a₂ = а = 42 мм < 0,2 h = 0,2 × 300 = 60 мм, корректировка значения a_crc, согласно п. 4.8а, не производится.

По формуле (256) определим значение М_о, предварительно вычислив:

M_o = M_crс + y bh² R_{bt, ser} = 34,8 ×10⁶ + 0,454 ×1150 ×300² ×1,15 = 88,8 ×10⁶ Н ×мм = 88,8 кН ×м.

Поскольку М_о = 88,8 кН ×м > M_r = 67 кН ×м, вычислим коэффициент j _b по формуле (253):

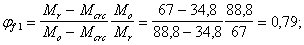
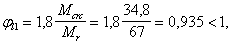
принимаем j _l1 = 1;

j_b = j _f1 j _l1 = 0,79 < 1.

С учетом коэффициента j_b, ширина раскрытия трещин равна a_crc = 0,34 ×0,79 = 0,269 мм < 0,3 мм, т. е. меньше предельно допустимого значения.

Пример 55. Дано: железобетонная колонна промышленного здания с размерами поперечного сечения h = 500 мм, b = 400 мм; a = a ¢ = 50 мм; бетон тяжелый класса В15 (R_b,ser = 11 МПа; R_bt,ser = 1,15 МПа; E_b = 2,05 ×10 ⁴ МПа); рабочая арматура класса A- III (Е _s = 2 ×10 ⁵ МПа); площадь ее сечения A_s = A ¢ _s = 1232 мм ² (2 Æ28); продольная сжимающая сила N = N_l = 500 кН; момент от полной нагрузки M_tot = 240 кН ×м, в том числе момент от постоянных и длительных нагрузок M_l = 150 кН ×м.

Требуется рассчитать колонну по раскрытию трещин.

Расчет. h _o = h ‑ a = 500 ‑ 50 = 450 мм. Определим необходимость расчета по раскрытию трещин. Для этого проверим условие (233). Так как то, согласно п. 4.2, момент сопротивления W_pl находим как для бетонного сечения. Используя формулу (246), находим

M_crc = 0,292 bh²R_bt,ser = 0,292 × 400 × 500² × 1,15 = 33,6 ×10 ⁶ Н ×мм.

Ядровое расстояние r определим по формуле (241). Для этого вычислим s _b как для упругого тела (влиянием арматуры пренебрежем):

принимаем j = 0,7;

.

По формуле (238) определим момент M_r:

т. е. условие (233) не выполняется. Следовательно, проверка раскрытия трещин обязательна.

Поскольку согласно п. 4,6 проверим непродолжительное раскрытие трещин. Для этого в соответствии с п. 4.10 предварительно вычислим ширину продолжительного раскрытия трещин от действия усилий M_l и N_l по формуле (249). При этом воспользуемся упрощенной формулой (264) для s _s.

По вычисленным значениям j _f = 0,074, m a = 0,067 и находим по табл. 30 значение коэффициента j _crc = 0,33.

Согласно п. 4.7, s = 1,0; h = 1,00;

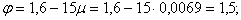
Напряжение в арматуре s _s от действия всех нагрузок так же определим по формуле (264).

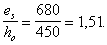
При j _f = 0,074, m a = 0,067 и коэффициент j _crc согласно табл. 30 равен 0,522.

Тогда, согласно формуле (265),

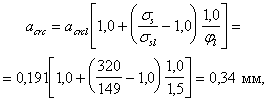
что меньше предельно допустимого значения a_crcl = 0,4 мм (см. табл. 1, поз. 4).

Пример 56. Дано: свободно опертая балка перекрытия пролетом l = 5,5 м, нагруженная равномерно распределенными нагрузками: временной длительно действующей эквивалентной нагрузкой v = 30 кН/м и постоянной нагрузкой g = 12,5 кН/м; размеры поперечного сечения b = 200 мм, h = 400 мм, h_о = 370 мм; бетон тяжелый класса В 15 (R_bt,ser = 1,15 МПа; E_b = 2,05 ×10 ⁴ МПа); хомуты двухветвевые из арматуры класса А- I (Е _s = 2,1 ×10 ⁵МПа) с шагом s = 150 мм, диаметром 8 мм (4 _sw = 101 мм ²).

Требуется произвести расчет по раскрытию наклонных трещин.

Расчет. Определим сначала необходимость расчета по раскрытию наклонных трещин, проверив условие (248).

Наибольшая поперечная сила в опорном сечении равна:

Согласно табл. 21, j _b3 = 0,6.

j _b3 R_bt,serbh_o = 0,6 × 15 × 200 × 370 = 51060 H < Q_max = 117 кН,

т. е. наклонные трещины образуются и расчет по ихраскрытию необходим.

Расчет производим согласно п. 4.11. Определим значения Q и Q_b1.

q₁ = g + v /2 = 12,5 + 30/2 = 27,5 кН/м;

j _b4 = 1,5 (см. табл. 21).

Поскольку 0,2 j _b4 R_bt,serb = 0,2 ×1,5 ×1,15 ×200 = 56,9 Н/мм > q₁ = 27,5 Н/мм, значение с при определении Q_b1 и Q принимаем равным с = 2 h _о = = 2 ×370 = 740 мм.

Отсюда

Q = Q_max ¾ q_1s = 117 ¾ 27,5 0,740 = 96,65 кН.

Определим напряжение в хомутах по формуле (267):

Согласно пп. 4.7 и 4.11, j _l = 1,5; h = 1,3; d_w = 8 мм.

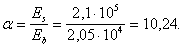
Определим ширину раскрытия наклонных трещин по формуле (266):

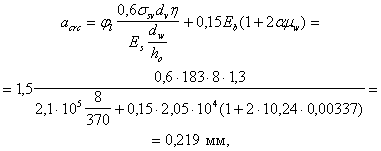
что меньше предельно допустимого значения а_{с rc} = 0,3 мм (см. табл. 1).

Не нашли, что искали? Воспользуйтесь поиском: