
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Определение кривизны железобетонных элементов на участках с трещинами в растянутой зоне
4.15 (4.27). На участках, где в растянутой зоне образуются нормальные к продольной оси элемента трещины, кривизна изгибаемых, внецентренно сжатых, а также внецентренно растянутых при eо ³ 0,8 ho элементов прямоугольного, таврового и двутаврового (коробчатого) сечений должна определяться по формуле
 (271)
(271)
Для изгибаемых элементов последнее слагаемое правой части формулы (271) принимается равным нулю. Знак «минус» в этой формуле принимается при внецентренном сжатии, знак «плюс» — при внецентренном растяжении.
В формуле (271):
М s — момент относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести площади сечения арматуры S, от всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, равный:
для изгибаемых элементов М s = М;
для внецентренно сжатых и внецентренно растянутых элементов М s = Nes;
z ¾ расстояние от центра тяжести площади сечения арматуры S до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной (плечо внутренней пары сил), определяемое согласно указаниям п. 4.16;
y s — коэффициент, учитывающий работу растянутого бетона на участке с трещинами и определяемый согласно указаниям п. 4.17;
y b — коэффициент, учитывающий неравномерность распределения деформаций крайнего сжатого волокна бетона по длине участка с трещинами и принимаемый равным:
для тяжелого, мелкозернистого и легкого бетонов
класса В10 и выше...............................................................0,9
для легкого и поризованного бетонов класса В7,5 и ниже... 0,7
j f ¾ коэффициент, определяемый по формуле (277);
x = x/ho — определяется согласно указаниям п. 4.16;
v ¾ коэффициент, характеризующий упруго-пластическое состояние бетона сжатой зоны и принимаемый равным:
при непродолжительном действии нагрузки ¾ коэффициенту vsh = 0,45;
при продолжительном действии нагрузки ¾ коэффициенту vl, определяемому по табл. 31.
Для изгибаемых и внецентренно сжатых элементов из тяжелого бетона при Mr < Mo кривизну допускается определять с учетом работы растянутого бетона над трещинами по формуле
 (272)
(272)
где
 (273)
(273)
 ¾ кривизна, определенная по формуле (271) при моменте М s,
¾ кривизна, определенная по формуле (271) при моменте М s,
равном:
для изгибаемых элементов М s = М o;
для внецентренно сжатых элементов Ms = М o + Nу sr;
у sr = yo ‑ а + r — расстояние от центра тяжести растянутой арматуры до оси, проходящей через наиболее удаленную ядровую точку (см. п. 4.2);
М r — момент, определяемый согласно п. 4.2 от полной нагрузки, включающей постоянную, длительную и кратковременные нагрузки;
М o ¾ момент, при котором растянутый бетон над трещинами выключается из работы, определяемый по формуле (256), в которой y уменьшается вдвое при учете продолжительного действия постоянных и длительных нагрузок;
Mcrc,r ¾ см. п. 4.2;
M, Mtot — моменты внешних сил относительно оси, проходящей через центр тяжести сечения, соответственно от рассматриваемой и от полной нагрузки;
j b1, j b2 — см. п. 4.14; при непродолжительном действии нагрузки j b2 = 1,0.
4.16(4.28). Значение x вычисляется по формуле
 (274)
(274)
но принимается не более 1,0, при этом es/ho принимается не менее 0,5.
Для изгибаемых элементов последнее слагаемое правой части формулы (274) принимается равным нулю.
В формуле (274) верхние знаки принимаются при сжимающем, а нижние — при растягивающем усилии N.
В формуле (274):
b — коэффициент, принимаемый равным для бетона:
тяжелого и легкого................................................ 1,8
мелкозернистого.................................................... 1,6
поризованного........................................................ 1,4
 (275)
(275)
 (276)
(276)
 ; (277)
; (277)
 . (278)
. (278)
Значение z вычисляется по формуле
 (279)
(279)
Для элементов прямоугольного сечения и таврового сечения с полкой в растянутой зоне в формулы (276)  и (279) вместо h ¢ f подставляются значения 2 a' или h ¢ f = 0 соответственно при наличии или отсутствии арматуры S ¢.
и (279) вместо h ¢ f подставляются значения 2 a' или h ¢ f = 0 соответственно при наличии или отсутствии арматуры S ¢.
Если  , то для изгибаемых элементов при j f ³ j f1, где
, то для изгибаемых элементов при j f ³ j f1, где  , значения z и
, значения z и  — определяются при
— определяются при  и j f = j f1, а при j f < j f1, значения j f, x, z и
и j f = j f1, а при j f < j f1, значения j f, x, z и  — определяются без учета арматуры S ¢. Для внецентренно нагруженных элементов при
— определяются без учета арматуры S ¢. Для внецентренно нагруженных элементов при  допускается всегда значения j f, x, z и
допускается всегда значения j f, x, z и  определять без учета арматуры S ¢.
определять без учета арматуры S ¢.
Расчет сечений, имеющих полку в сжатой зоне, при 
производится как прямоугольных шириной b ¢ f.
Расчетная ширина полки b ¢f определяется согласно указаниям п. 3.23.
Для внецентренно сжатых элементов значение z должно приниматься не более 0,97 es.
4.17 (4.29). Коэффициент y s определяется по формуле
 (280)
(280)
но не более 1,0, при этом следует принимать es/ho ³ 1,2/ j ls.
Для изгибаемых элементов последний член в правой части формулы (280) принимается равным нулю.
В формуле (280):
j ls ¾ коэффициент, учитывающий влияние длительности действия нагрузки и принимаемый по табл. 32;
 (281)
(281)
Таблица 32(36)
| Длительность действия | Коэффициент j ls при классе бетона | |
| нагрузки | В 10 и выше | В7,5 и ниже |
| 1. Непродолжительное действие при арматуре классов: | ||
| А- II, А- III | 1,1 | 0,8 |
| А- I, Вр- I | 1,0 | 0,7 |
| 2. Продолжительное действие | 0,8 | 0,6 |
но не более 1,0;
здесь Wpl ¾ см. п. 4.3;
Mr — см. п. 4.2.
4.18. Кривизна внецентренно растянутых элементов с продольной силой N, приложенной между центрами тяжести площадей арматуры S и S ¢, на участках с нормальными трещинами в растянутой зоне определяется по формуле
 (282)
(282)
где zs = ho ‑ a ¢ — расстояние между центрами тяжести площадей арматуры S и S';
y s, y ¢ s — коэффициенты, учитывающие работу растянутого бетона соответственно для арматуры S и S ¢ и определяемые по формулам:
 (283)
(283)
 (284)
(284)
здесь j ls ¾ коэффициент, принимаемый равным при действии нагрузки:
непродолжительном........................................... 0,70
продолжительном............................................... 0,35
Ncrc, N ¢ crc ¾ усилия, приложенные в той же точке, что и сила N, и соответствующие образованию трещин соответственно в более и менее растянутой зонах сечения; значения Ncrc и N ¢ crc определяются по формулам:
 . (285)
. (285)
и принимаются не более N; кроме того, при r' < ео значение N ¢crc принимается равным N.
В формулах (285):
Wpl, W ¢ pl ¾ значения Wpl, определенные согласно п. 4.3 соответственно для более и менее растянутой сторон сечения;
r, r ¢ ¾ расстояния от центра тяжести приведенного сечения до ядровых точек, наиболее удаленных соответственно от более и менее растянутой сторон сечения; значения r и r ¢ определяются по формуле (242).
4.19. Кривизна внецентренно растянутых элементов с продольной силой N, приложенной вне расстояния между центрами тяжести площадей арматуры S и S ¢, и при eо < 0,8 hо определяется линейной интерполяцией между кривизной  , определенной по формуле (282) при е s = 0 (т.е. при eо = yso, где yso — расстояние от центра тяжести площади арматуры S до центра тяжести приведенного сечения), и кривизной
, определенной по формуле (282) при е s = 0 (т.е. при eо = yso, где yso — расстояние от центра тяжести площади арматуры S до центра тяжести приведенного сечения), и кривизной 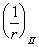 , определенной по формуле (271) е s = 0,8 ho ‑ yso (т.е. при ео = 0,8 hо ‑ yso. Тогда значение кривизны равно:
, определенной по формуле (271) е s = 0,8 ho ‑ yso (т.е. при ео = 0,8 hо ‑ yso. Тогда значение кривизны равно:
 (286)
(286)
4.20. Для элементов прямоугольного сечения с симметричной арматурой, испытывающих косое внецентренное сжатие, кривизны вычисляются по формуле
 (287)
(287)
где  — кривизна, вычисленная как для плоского внецентренного сжатия согласно пп. 4.15-4.17 в предположении действия силы N с эксцентриситетом е o в плоскости оси симметрии сечения х, при этом принимается, что силовая плоскость расположена между осью х и диагональю сечения;
— кривизна, вычисленная как для плоского внецентренного сжатия согласно пп. 4.15-4.17 в предположении действия силы N с эксцентриситетом е o в плоскости оси симметрии сечения х, при этом принимается, что силовая плоскость расположена между осью х и диагональю сечения;
j b — коэффициент, учитывающий влияние угла наклона силовой плоскости на величину деформаций кососжимаемых элементов и определяемый по формуле
 ; (288)
; (288)

здесь 
 ¾ площади арматуры, расположенной у грани сечения, нормальной к осям соответственно х и у, при этом угловой стержень учитывается как при вычислении mх, так и mу;
¾ площади арматуры, расположенной у грани сечения, нормальной к осям соответственно х и у, при этом угловой стержень учитывается как при вычислении mх, так и mу;
hх, hy — размеры сечения в направлении осей соответственно х и у;
b — угол наклона силовой плоскости (плоскости эксцентриситета силы N) к плоскости оси х, рад.
Плоскость деформирования составляет с плоскостью оси х угол g, определяемый из равенства
 (289)
(289)
где Ix, Iy ¾ моменты инерции приведенного сечения относительно осей соответственное y и х.
Кривизны в плоскостях х и у при косом внецентренном сжатии равны:
 , (29 0)
, (29 0)
 (291)
(291)
где  — определяется по формуле (287).
— определяется по формуле (287).
4.21 (4.30). Полная кривизна  — для участка с трещинами в растянутой зоне должна определяться по формуле
— для участка с трещинами в растянутой зоне должна определяться по формуле
 (292)
(292)
где  ¾ кривизна от непродолжительного действия всей нагрузки, на которую производится расчет по деформациям согласно указаниям п.1.17;
¾ кривизна от непродолжительного действия всей нагрузки, на которую производится расчет по деформациям согласно указаниям п.1.17;
 — кривизна от непродолжительного действия постоянных и длительных нагрузок;
— кривизна от непродолжительного действия постоянных и длительных нагрузок;
 — кривизна от продолжительного действия постоянных и длительных нагрузок.
— кривизна от продолжительного действия постоянных и длительных нагрузок.
Кривизны  ,
,  и
и  определяются по формулам (271), (272), (282), (286) и (287), при этом
определяются по формулам (271), (272), (282), (286) и (287), при этом  и
и  вычисляются при значениях y s и v, отвечающих непродолжительному действию нагрузки, а
вычисляются при значениях y s и v, отвечающих непродолжительному действию нагрузки, а  — при y s и v, отвечающих продолжительному действию нагрузки. Если значения
— при y s и v, отвечающих продолжительному действию нагрузки. Если значения  и
и  оказываются отрицательными, они принимаются равными нулю.
оказываются отрицательными, они принимаются равными нулю.
Не нашли, что искали? Воспользуйтесь поиском: