
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ОПРЕДЕЛЕНИЕ ПРОГИБОВ
4.29. Для изгибаемых элементов при прогиб f определяется следующим образом:
а) для элементов постоянного сечения, работающих как свободно опертые или консольные балки, ¾ по формуле
(311)
где ¾ кривизна в сечении с наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб;
р m — коэффициент, принимаемый по табл. 35;
Таблица 34
| Коэф фици енты | Коэффициент j 1 при значениях m a, равных | Коэффициент j 2 при значениях m a, равных | ||||||||||||||||||||||
| j ft | j f | 0,02 | 0,03 | 0,04 | 0,05 | 0,06 | 0,07 | 0,08 | 0,10 | 0,13 | 0,15 | 0,17 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 | <0,04 | 0,04-0,08 | 0,08-0,15 | 0,15-0,30 | 0,30-0,50 |
| Продолжительное действие нагрузки | ||||||||||||||||||||||||
| 0,0 0,0 0,0 0,0 0,0 0,0 | 0,0 0,2 0,4 0,6 0,8 1,0 | 0,43 0,49 0,52 0,54 0,56 0,57 | 0,39 0,46 0,49 0,51 0,53 0,54 | 0,36 0,44 0,47 0,49 0,51 0,52 | 0,34 0,42 0,46 0,48 0,49 0,51 | 0,32 0,41 0,45 0,47 0,48 0,50 | 0,30 0,39 0,44 0,46 0,47 0,49 | 0,28 0,37 0,42 0,44 0,46 0,48 | 0,26 0,35 0,40 0,43 0,45 0,47 | 0,23 0,31 0,38 0,42 0,44 0,46 | 0,22 0,29 0,35 0,39 0,42 0,44 | 0,21 0,27 0,33 0,37 0,40 0,42 | 0,19 0,25 0,31 0,35 0,38 0,41 | 0,16 0,21 0,26 0,31 0,35 0,38 | 0,14 0,19 0,24 0,28 0,32 0,35 | 0,13 0,17 0,22 0,25 0,29 0,32 | 0,12 0,16 0,20 0,23 0,27 0,30 | 0,11 0,14 0,18 0,22 0,25 0,28 | 0,10 0,13 0,17 0,20 0,23 0,26 | 0,10 0,12 0,13 0,13 0,14 0,15 | 0,07 0,09 0,10 0,11 0,12 0,13 | 0,04 0,05 0,06 0,08 0,09 0,10 | 0,00 0,00 0,02 0,02 0,04 0,06 | 0,00 0,00 0,00 0,00 0,00 0,00 |
| 0,2 0,4 0,6 0,8 1,0 | 0,0 0,0 0,0 0,0 0,0 | 0,47 | 0,40 0,42 0,43 | 0,36 0,36 0,37 0,38 0,40 | 0,33 0,33 0,33 0,33 0;33 | 0,31 0,31 0,31 0,30 0,30 | 0,30 0,30 0,30 0,29 0,29 | 0,28 0,28 0,27 0,27 0,27 | 0,26 0,26 0,25 0,24 0,24 | 0,23 0,22 0,22 0,22 0,22 | 0,22 0,21 0,21 0,21 0,20 | 0,21 0,20 0,20 0,20 0,19 | 0,19 0,19 0,18 0,17 0,17 | 0,16 0,16 0,15 0,15 0,15 | 0,14 0,14 0,14 0,14 0,14 | 0,13 0,13 0,12 0,12 0,12 | 0,11 0,11 0,11 0,11 0,11 | 0,11 0,10 0,10 0,10 0,10 | 0,10 0,10 0,10 0,10 0,10 | 0,15 0,18 0,20 0,23 0,25 | 0,12 0,16 0,19 0,22 0,24 | 0,08 0,13 0,17 0,20 0,23 | 0,03 0,06 0,09 0,12 0,14 | 0,00 0,02 0,03 0,05 0,06 |
| 0,2 0,4 0,6 0,8 1,0 | 0,2 0,4 0,6 0,8 1,0 | 0,51 | 0,45 0,53 | 0,43 0,49 0,53 | 0,40 0,47 0,50 0,53 0,61 | 0,38 0,45 0,48 0,50 0,53 | 0,37 0,43 0,46 0,48 0,50 | 0,36 0,42 0,44 0,46 0,48 | 0,34 0,39 0,41 0,44 0,45 | 0,30 0,37 0,39 0,41 0,43 | 0,28 0,35 0,38 0,39 0,40 | 0,26 0,33 0,36 0,38 0,39 | 0,24 0,30 0,34 0,37 0,38 | 0,21 0,26 0,31 0,34 0,36 | 0,19 0,23 0,28 0,31 0,34 | 0,17 0,21 0,25 0,29 0,32 | 0,16 0,20 0,23 0,26 0,29 | 0,14 0,18 0,21 0,25 0,27 | 0,13 0,17 0,20 0,23 0,26 | 0,16 0,20 0,24 | 0,13 0,19 0,22 0,25 0,26 | 0,08 0,14 0,20 0,24 0,25 | 0,04 0,07 0,12 0,19 0,20 | 0,00 0,03 0,04 0,08 0,12 |
| Непродолжительное действие нагрузки | ||||||||||||||||||||||||
| 0,0 0,0 0,0 0,0 0,0 0,0 | 0,0 0,2 0,4 0,6 0,8 1,0 | 0,64 0,72 0,76 0,79 0,82 0,84 | 0,59 0,66 0,69 0,71 0,73 0,74 | 0,56 0,63 0,66 0,69 0,70 0,71 | 0,53 0,61 0,65 0,67 0,68 0,69 | 0,51 0,59 0,63 0,65 0,67 0,68 | 0,50 0,58 0,62 0,64 0,66 0,67 | 0,49 0,57 0,61 0,63 0,65 0,66 | 0,46 0,56 0,60 0,63 0,65 0,66 | 0,43 0,53 0,59 0,62 0,64 0,66 | 0,41 0,51 0,57 0,61 0,63 0,65 | 0,40 0,49 0,56 0,60 0,63 0,65 | 0,37 0,46 0,53 0,58 0,61 0,63 | 0,34 0,43 0,49 0,55 0,58 0,61 | 0,32 0,40 0,46 0,52 0,56 0,59 | 0,30 0,37 0,44 0,49 0,53 0,56 | 0,28 0,35 0,41 0,46 0,50 0,54 | 0,26 0,33 0,39 0,44 0,48 0,52 | 0,25 0,31 0,37 0,42 0,46 0,50 | 0,17 0,21 0,23 0,25 0,26 0,27 | 0,14 0,18 0,20 0,21 0,23 0,24 | 0,09 0,11 0,14 0,16 0,17 0,18, | 0,02 0,03 0,04 0,05 0,06 0,07 | 0,00 0,00 0,00-0,00 0,00 0,00 |
| 0,2 0,4 0,6 0,8 1,0 | 0,0 0,0 0,0 0,0 0,0 | 0,74 | 0,60 0,63 0,81 | 0,56 0,57 0,59 0,63 0,84 | 0,53 0,54 0,54 0,55 0,57 | 0,51 0,51 0,51 0,51 0,52 | 0,49 0,49 0,49 0,49 0,49 | 0,47 0,47 0,47 0,47 0,47 | 0,44 0,44 0,44 0,44 0,44 | 0,42 0,42 0,42 0,42 0,42 | 0,40 0,40 0,40 0,40 0,40 | 0,39 0,39 0,39 0,39 0,39 | 0,37 О,Э7 0,37 0,37 0,37 | 0,34 0,34 0,34 0,34 0,34 | 0,32 0,32 0,32 0,32 0,32 | 0,30 0,30 0,30 0,30 0,30 | 0,28 0,28 0,28 0,28 0,28 | 0,26 0,26 0,26 0,26 0,27 | 0,25 0,25 0,25 0,25 0,25 | 0,28 0,35 0,36 0,45 0,50 | 0,23 0,31 0,39 0,40 0,46 | 0,16 0,25 0,32 0,38 0,44 | 0,07 0,14 0,20 0,25 0,29 | 0,00 0,03 0,08 0,12 0,15 |
| 0,2 0,4 0,6 0,8 1,0 | 0,2 0,4 0,6 0,8 1,0 | 0,79 | 0,67 0,77 | 0,63 0,69 0,76 | 0,61 0,66 0,70 0,76 0,92 | 0,59 0,64 0,67 0,71 0,76 | 0,58 0,62 0,65 0,68 0,71 | 0,56 0,61 0,64 0,66 0,69 | 0,55 0,58 0,61 0,64 0,66 | 0,52 0,56 0,58 0,61 0,63 | 0,50 0,55 0,57 0,59 0,61 | 0,48 0,54 0,56 0,58 0,60 | 0,46 0,52 0,55 0,57 0,58 | 0,42 0,48 0,53 0,56 0,57 | 0,39 0,45 0,50 0,53 0,56 | 0,37 0,43 0,47 0,51 0,54 | 0,35 0,40 0,45 0,49 0,52 | 0,33 0,38 0,43 0,47 0,50 | 0,31 0,37 0,41 0,45 0,48 | 0,27 0,39 0,50 | 0,24 0,37 0,46 0,60 0,72 | 0,17 0,30 0,44 0,57 0,70 | 0,08 0,16 0,28 0,41 0,55 | 0,00 0,04 0,11 0,21 0,31 |
при схеме загружения свободно опертой или консольной балки, не приведенной в табл. 35, прогиб определяется по формулам сопротивления материалов при жесткости, равной отношению наибольшего момента к наибольшей кривизне;
б) если прогиб, определенный по подпункту «а», превышает допустимый, то для слабоармированных элементов (m £ 0,5 %) его значение рекомендуется уточнять за счет учета повышенной жесткости на участках без трещин при переменной жесткости на участке с трещинами; для свободно опертых балок, загруженных равномерно распределенной нагрузкой, это соответствует формуле
(312)
где р crc — коэффициент, принимаемый по табл. 36 в зависимости от отношения Mcrc / Mtot (Mcrc ¾ см. пп. 4.2 и 4.3);
— кривизна в сечении с наибольшим моментом, определенная как для сплошного тела по формуле (270), от нагрузки, при которой определяется прогиб; допускается значение Ired в формуле (270) определять как для бетонного элемента.
Для иных схем загружения величина f может быть определена по формуле (314);
в) для изгибаемых элементов с защемленными опорами прогиб в середине пролета определяется по формуле
(313)
где — кривизны элемента соответственно в середине пролета, на левой и правой опорах;
р m ¾ коэффициент, определяемый по табл. 35 как для свободно опертой балки;
г) для элементов переменного сечения, а также в тех случаях, когда требуется более точное, чем по формулам (311) и (313), определение прогибов, а сами элементы и нагрузка симметричны относительно середины пролета, прогиб определяется по формуле
Таблица 35
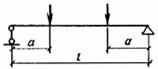
| Схема загружения консольной балки | Коэффициент Рт | Схема загружения свободно опертой балки | Коэффициент Рт |
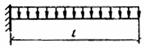
| 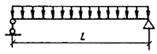
| ||

| 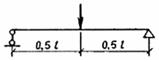
| ||
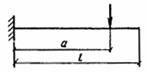
| 
|
Примечание. При загружении элемента одновременно по нескольким схемам (где pm1 и M1, pm2 и M2 и т. д. ¾ соответственно коэффициент pm, и наибольший изгибающий момент М для каждой схемы загружения). В этом случае в формулах (311) ¾ (313) величина определяется при значении М, равном сумме наибольших изгибающих моментов, определенных для каждой схемы загружения.
Таблица 36
| Mcrc/Mtot | 1,00 | 0,99 | 0,98 | 0,96 | 0,94 | 0,92 | 0,90 | 0,85 | 0,80 |
| Pcrc | 0,104 | 0,088 | 0,082 | 0,073 | 0,067 | 0,062 | 0,058 | 0,049 | 0,042 |
Продолжение табл. 36
| Mcrc/Mtot | 0,75 | 0,70 | 0,60 | 0,50 | 0,40 | 0,30 | 0,20 | 0,10 | 0,00 |
| Pcrc | 0,036 | 0,032 | 0,024 | 0,018 | 0,013 | 0,008 | 0,005 | 0,002 | 0,000 |
где
(314)
где — кривизны соответственно на опоре, на расстоянии от опоры, на расстоянии от опоры и в середине пролета; значения кривизн подсчитываются со своими знаками согласно эпюре кривизн.
В остальных случаях прогиб в середине пролета рекомендуется определять по формуле (294).
Входящие в формулы (311) ¾ (314) значения кривизн определяются по формулам (271), (272), (282), (286), (309) и (310) при наличии трещин в растянутой зоне и по формулам (269) и (270) — при их отсутствии.
Для сплошных плит толщиной менее 250 мм необходимо учитывать указания п. 4.24.
4.30. Для коротких элементов (l / h < 10) постоянного сечения, работающих как свободно опертые балки, прогиб вычисляется согласно п. 4.29 и умножается на коэффициент Pq, учитывающий влияние деформаций сдвига. Коэффициент Pq определяется по формуле
(315)
где j q = 0,5 — при отсутствии как нормальных, так и наклонных трещин, т.е. при выполнении условий (233) и (248);
j q = 1,5 — при наличии нормальных или наклонных трещин;
р m — см. табл. 35.
Примеры расчета
Пример 5 7. Дано: железобетонная плита перекрытия гражданского здания прямоугольного сечения размерами h = 120 мм, b = 1000 мм, ho = 105 мм; пролет l = 3,1 м; бетон тяжелый класса В25 (Eb =2,7 ×10 4 МПа; Rbt.ser = 1,6 МПа); растянутая арматура класса А- II (Е s = 2,1 ×10 5 МПа), площадь ее поперечного сечения А s = 393 мм 2 (5 Æ 10); полная равномерно распределенная нагрузка qtot = 7 кН/м, в том числе ее часть от постоянных и длительных нагрузок ql = 6 кН/м; прогиб ограничивается эстетическими требованиями.
Требуется рассчитать плиту по деформациям.
Расчет. Определим необходимость расчета плиты по деформациям согласно п. 4.27:
Из табл. 33 по m a = 0,029 и j f = j ft = 0 находим l lim = 21. Так как h < 250 мм, то l lim корректируем путем деления на коэффициент Тогда
Учитывая примечание к п. 4.27 (случай «а»), имеем
Поскольку - расчет по деформациям необходим.
Определим кривизну в середине пролета от действия момента М l (так как прогиб ограничивается эстетическими требованиями).
Принимаем без расчета, что элемент имеет трещины в растянутой зоне, в связи с чем кривизну определим по формуле (309).
Из табл. 34 по m a = 0,028 и j f = j ft = 0 находим значения j 1 = 0,393 и j 2 = 0,10, соответствующие продолжительному действию нагрузки.
Прогиб определим согласно п. 4.29а, принимая, согласно табл. 35,:
Так как h < 250 мм, полный прогиб равен f = 13,5 × 1,23 = 16,6 мм, что больше предельно допустимого прогиба (см. табл. 2).
Поскольку m = 0,00375 < 0,005, согласно п. 4.29 б уточним значение f по формуле (312). Для этого вычислим величины и Mcrc.
Так как рассчитывается слабоармированный элемент (m < 0,01), Ired и М crc определим как для бетонного сечения (см. пп. 4.2 и 4.3):
j b1 = 0,85 (как для тяжелого бетона);
Коэффициент рс rс определим по табл. 36 при
.
С учетом поправки на малую высоту сечения (h < 250 мм) f = 9,84 ×1,23 = 12,1 мм, что меньше предельно допустимого прогиба f = 15,5 × мм.
Поскольку l/h > 10, влиянием деформаций сдвига пренебрегаем.
Пример 58: Дано: ригель перекрытия общественного здания прямоугольного сечения размерами b = 200 мм, h = 600 мм; a = 80 мм; пролет ригеля l = 4,8 м; бетон тяжелый класса В25 (Е b = 2,7 ´ 10 4 МПа; Rbt,ser = 1,6 МПа); рабочая арматура класса А- III (Es = 2 × 10 5 МПа), площадь ее поперечного сечения А s = 2463 мм (4 Æ28); полная равномерно распределенная нагрузка qtot = 85,5 кН/м, в том числе ее часть от постоянных и длительных нагрузок ql = 64 кН/м; прогиб ограничивается эстетическими требованиями; влажность воздуха в помещении свыше 40 %.
Требуется рассчитать ригель по деформациям.
Расчет. Определим необходимость расчета по деформациям согласно п. 4.27.
ho = 600 ‑ 80 = 520 мм;
Так как l/h = 4,8/0,6 = 8 < 10, необходимо учитывать влияние деформаций сдвига на прогиб элемента: l/ho = 4,8/0,52 = 9,3. По табл. 33 при m a = 0,176 и j f = j ft = 0 находим l lim = 8.
т. е. расчет по деформациям необходим.
Поскольку m = 0,238 > 0,005, согласно п. 4.1 кривизну определим с учетом наличия трещин в растянутой зоне. Так как прогиб ограничивается эстетическими требованиями, расчет производим на действие момента М l. Кривизну в середине пролета вычислим по формуле (309).
По табл. 34 при m a = 0,176 и j f = j ft = 0 находим j 1 = 0,206 и j 2 = 0.
Полный прогиб определим согласно пп. 4.29а и 4.30 с учетом влияния деформаций сдвига. Согласно табл. 35,
т. е. прогиб ригеля меньше предельно допустимого (см. табл. 2).
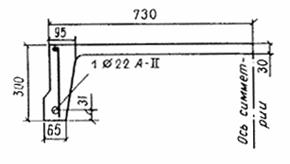
Пример 59. Дано: железобетонная плита покрытия с расчетным пролетом 5,7 м; размеры поперечного сечения (для половины сечения плиты) — по черт. 89; бетон легкий класса В25 (Rb,ser = 18,5 МПа; Rbt,ser = 1,6 МПа), марки по средней плотности D1600 (Eb =16,5 ×10 3 МПа); рабочая арматура класса А- II (Es = 2,1 ×10 5 МПа), площадь ее сечения As = 380 мм 2 (1 Æ22); постоянная и длительная равномерно распределенные нагрузки на плиту ql = 8,75 кН/м; прогиб плиты ограничивается эстетическими требованиями; помещение, перекрываемое плитой, имеет нормальную влажность воздуха (40 ¾ 75 %).
Требуется рассчитать плиту по деформациям.
Не нашли, что искали? Воспользуйтесь поиском: