
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример расчета и конструирование многопустотной панели
Требуется рассчитать и сконструировать сборные железобетонные конструкции междуэтажного перекрытия гражданского здания при следующих данных: поперечный пролет l1= 6,4 м, продольный шаг внутренних колонн l2= 6 м кратковременная нагрузка на перекрытие pn =4000 H/м2. Несущими элементами перекрытия являются многопустотная панель с круглыми пустотами, имеющая номинальную длину 6,4 м, ширину 1,2 м, высоту 22 см, и многопролетный сборный ригель прямоугольного сечения. Панель опирается на ригель сверху. Действующие на перекрытие нагрузки указаны в таблице 1
Определение нагрузок и усилий. На 1 м длины панели шириной 120 см действуют следующие нагрузки, Н/м: кратковременная нормативная pn= 2800·1,2=3360, кратковременная расчетная p= 3640·1,2=4380, постоянная и длительная нормативная qn= 5450·1,2=6540; постоянная и длительная расчетная q= 6370·1,2=7650; итого нормативная qn+pn= 6540+3360=9900; итого расчетная q+p= 7650+4380=12030.
Расчетный изгибающий момент от полной нагрузки
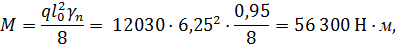
где l0= 6,4-0,2/2-0,1/2=6,25 м;
расчетный изгибающий момент от полной нормативной нагрузки (для расчета и трещиностойкости) при 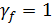 .
.

то же, от нормативной постоянной и длительной временной нагрузок

то же, от нормативной кратковременной нагрузки

Максимальная поперечная сила на опоре от расчетной нагрузки

то же, от нормативной нагрузки
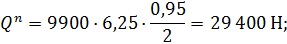
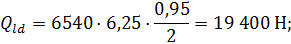
Таблица 1 – Нагрузки на сборное междуэтажное перекрытие
| Вид нагрузки | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке 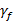
| Расчетная нагрузка, Н/м2 |
| Постоянная: От паркетного пола, t= 0,02 м, ρ=800 кг/м3 от шлакобетонного слоя, t=0,065 м, ρ=1600 кг/м3 от пенобетонной звукоизоляционной плиты, t= 0,06 м, ρ=500 кг/м3 от железобетонной панели (по каталогу) приведенной толщиной 110 мм, t= 0,11 м, ρ=2500 кг/м3 | 1,1 1,2 1,2 1,1 | ||
| Итого Временная: кратковременная длительная | 
| – 1,3 1,3 | q= 4810 |
| Итого Полная нагрузка: постоянная и длительная кратковременная | 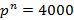
| – – – | p= 5200 |
| Итого | 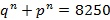
| – | q+p= 10 010 |
Подбор сечений. Для изготовления сборной панели принимаем: бетон класса В30, Eb= 32,5  104 МПа, Rb= 17 МПа, Rbt= 1,2 МПа, γ b2= 0,9; продольную арматуру – из стали класса А-II, Rs =280 МПа, поперечную арматуру – из стали класса А-I, Rs =225 МПа и Rsw =175 МПа; армирование – сварными сетками и каркасами; сварные сетки в верхней и нижней полках панели – из проволоки класса Вр-I, Rs =360 МПа при d= 5мм и Rs =265 МПа при d= 4мм.
104 МПа, Rb= 17 МПа, Rbt= 1,2 МПа, γ b2= 0,9; продольную арматуру – из стали класса А-II, Rs =280 МПа, поперечную арматуру – из стали класса А-I, Rs =225 МПа и Rsw =175 МПа; армирование – сварными сетками и каркасами; сварные сетки в верхней и нижней полках панели – из проволоки класса Вр-I, Rs =360 МПа при d= 5мм и Rs =265 МПа при d= 4мм.
Панель рассчитываем как балку прямоугольного сечения с заданными размерами b  h= 120
h= 120  22 см (где b – номинальная ширина; h – высота панели). Проектируем панель шестипустотной. В расчете поперечное сечение пустотной панели приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции. Вычисляем:
22 см (где b – номинальная ширина; h – высота панели). Проектируем панель шестипустотной. В расчете поперечное сечение пустотной панели приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции. Вычисляем:
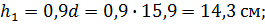

Приведенная толщина ребер  (расчетная ширина сжатой полки
(расчетная ширина сжатой полки  ).
).
Расчет по прочности нормальных сечений. Предварительно проверяемвысоту сечения панели перекрытия из условия обеспечения прочности при соблюдении необходимой жестокости по формуле:

где 
Принятая высота сечения h= 22 см достаточна. Отношение  в расчет вводим всю ширину полки
в расчет вводим всю ширину полки  Вычисляем по формуле:
Вычисляем по формуле:

где h0=h-a= 22-3=19 см.
По табл. находим 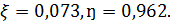 Высота сжатой зоны
Высота сжатой зоны  - нейтральная ось проходит в пределах сжатой полки. Площадь сечения продольной арматуры
- нейтральная ось проходит в пределах сжатой полки. Площадь сечения продольной арматуры
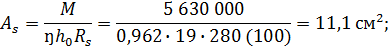
предварительно принимаем 6Ø16А-II, As= 12,06 см2, а также учитываем сетку С-I 5Вр-I-250/4Вр-I-250 1170·6350 25/20 (ГОСТ 8478-81), As1= 6·0,116=1,18 см2; 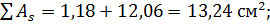 стержни диаметром 16 мм распределяем по два в крайних ребрах и два в одном среднем ребре.
стержни диаметром 16 мм распределяем по два в крайних ребрах и два в одном среднем ребре.
Расчет по прочности наклонных сечений. Проверяем условие необходимости постановки поперечной арматуры для многопустотных панелей, Qmax= 35,5 кН.
Вычисляем проекцию с наклонного сечения по формуле:

где  - для тяжелого бетона;
- для тяжелого бетона;  – коэффициент, учитывающий влияние свесов сжатых полок; в многопустотной плите при семи ребрах
– коэффициент, учитывающий влияние свесов сжатых полок; в многопустотной плите при семи ребрах

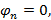 ввиду отсутствия усилий обжатия значение
ввиду отсутствия усилий обжатия значение 
В расчетном наклонном сечении 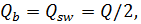 следовательно,
следовательно,  Принимаем c= 38 см, тогда
Принимаем c= 38 см, тогда  Следовательно, поперечная арматура по расчету не требуется.
Следовательно, поперечная арматура по расчету не требуется.
Поперечную арматуру предусматриваем из конструктивных условий, располагая ее с шагом

Назначаем поперечные стержни диаметром 6 мм класса А-I через 10 см у опор на участках длиной ¼ пролета. В средней ½ части панели для связи продольных стержней каркаса по конструктивным соображениям ставим поперечные стержни через 0,5 м. Если в нижнюю сетку С-I включить рабочие продольные стержни, то приопорные каркасы можно оборвать в ¼ пролета панели.
Определение прогибов. Момент в середине пролета от полной нормативной нагрузки Mn =46 000 Н 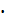 м; от постоянной и длительной нагрузок Mld =30 500 Н
м; от постоянной и длительной нагрузок Mld =30 500 Н  м; от кратковременной нагрузки Mcd =15 600 Н
м; от кратковременной нагрузки Mcd =15 600 Н  м.
м.
Определим прогиб панели приближенным методом, используя значения λlim. Для этого предварительно вычислим:


По таблице 2 находим λlim=16 при 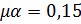 и арматуре класса А-II.
и арматуре класса А-II.
Таблица 2– Значения коэффициента λlim для случаев, когда проверка прогиба не требуется
| γ/ | γ | Класс арматуры | Значения λlim при μα | ||||||||||||
| 0,02 | 0,04 | 0,07 | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | |||||||
| А=II A=III | |||||||||||||||
| 0,2 | А=II A=III | ||||||||||||||
| 0,4 | А=II A=III | ||||||||||||||
| 0,6 | А=II A=III | ||||||||||||||
| 0,8 | А=II A=III | ||||||||||||||
| 1,0 | А=II A=III | ||||||||||||||
| 0,2 | А=II A=III | ||||||||||||||
| 0,6 | А=II A=III | ||||||||||||||
| 1,0 | А=II A=III | ||||||||||||||
| 0,2 | 0,2 | А=II A=III | |||||||||||||
| 0,6 | 0,6 | А=II A=III | |||||||||||||
| 1,0 | 1,0 | А=II A=III | |||||||||||||
Общая оценка деформативности панели по формуле

так как  второй член левой части неравенства ввиду малости не учитываем и оцениваем по условию
второй член левой части неравенства ввиду малости не учитываем и оцениваем по условию 

условие не удовлетворяется, требуется расчет прогибов.
Прогиб в середине пролета панели по формуле от постоянных и длительных нагрузок

где  - кривизна в середине пролета, определяемая по формуле:
- кривизна в середине пролета, определяемая по формуле:

здесь коэффициенты 
Вычисляем прогиб f следующим образом:  , что меньше
, что меньше  для элементов перекрытий с плоским потолком при
для элементов перекрытий с плоским потолком при  (см. табл.3)
(см. табл.3)
Таблица 3 – Предельные прогибы железобетонных элементов
| Элементы конструкций | Предельно допустимые прогибы flim | Учитываемые нагрузки |
| 1. Подкрановые балки при кранах: ручных электрических | l/ 500 l/ 600 | Постоянные, длительные и кратковременные |
2. Перекрытия с плоским потолком
и элементы покрытия (кроме указанных в
поз. 4) при пролетах, м:
l< 6
6 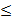 l l 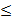 7,5
l> 7,5 7,5
l> 7,5
| l/ 200 3 см l/ 250 | Постоянные и длительные |
3. Перекрытия с ребристым потолком
и элементы лестниц при пролетах, м:
l< 5
 l l 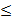 10
l> 10 10
l> 10
| l/ 300 2,5 см l/ 400 | То же |
4. Элементы покрытий с/х зданий
произв-го назначения при пролетах, м:
l< 6
6 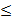 l l 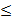 7,5
l> 7,5 7,5
l> 7,5
| l/ 150 4 см l/ 250 | » |
5. Навесные стеновые панели (при расчете
из плоскости) при пролетах, м:
l< 6
6 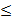 l l 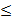 7,5
l> 7,5 7,5
l> 7,5
| l/ 200 3 см l/ 250 | Постоянные, длительные и кратковременные |
Расчет панели по раскрытию трещин. Панель перекрытия согласно таблице 4, относится к третьей категории трещиностойкости как элемент, эксплуатируемый в закрытом помещении и армированный стержнями из стали класса А-II. Предельно допустимая ширина раскрытия трещин acrc1= 0,4 мм и acrc2= 0,3 мм.
Для элементов третьей категории трещиностойкости, рассчитываемых по раскрытию трещин, нормальных к продольной оси, при действии кратковременных и длительных нагрузок должно соблюдаться условие
acrc=acrc1-acrc2+acrc3<acrc,max,
где acrc1-acrc2 – приращение ширины раскрытия трещин в результате кратковременного увеличения нагрузки от постоянной и длительной до полной; acrc3 – ширина раскрытия трещин от длительного действия постоянных и длительных нагрузок.
Таблица 4– Учет эксплуатационных нагрузок при расчете ж/б конструкций по трещиностойкости
| Категория требований к трещиностойкости ж/б конструкций | Нагрузки и коэффициенты надежности по нагрузке γ f, принимаемые при расчете | |||
| по образованию трещин | по раскрытию трещин | по закрытию трещин | ||
| непродолжительному | продолжительному | |||
| Постоянные, длительные и кратковременные при γ f >1,0⃰ | ̶ | ̶ | ̶ | |
| То же (расчет производится для выяснения необходимости проверки по непродолжительному раскрытию трещин и по их закрытию) | Постоянные, длительные и кратковременные при γ f= 1,0 | ̶ | Постоянные и длительные при γ f= 1,0 | |
| Постоянные, длительные и кратковременные при γ f= 1,0 (расчет производится для выяснения необходимости проверки по раскрытию трещин) | То же | Постоянные и длительные при γ f= 1,0 | ̶ |
⃰ Коэффициент γ f принимается, как при расчете по прочности
Ширину раскрытия трещин определяем по формуле

для вычисления acrc используем данные норм и величины, полученные при определении прогибов:
δ= 1 – как для изгибаемых элементов;
ɳ=1 – для стержневой арматуры периодического профиля;
d =1,6 см – по расчету;
Es =2,1·105 МПа – для стали класса А-II;
δa=1, так как a2 =3 см<0,2 /h= 0,2 ·22=4,4 см;
φ l =1 – при кратковременных нагрузках и φ l =1,6 – 15μ – при постоянных и длительных нагрузках;

принимаем μ=0,02 (см. СНиП 2.03.01 – 84), тогда φ l =1,6 – 15·0,02=1,3;
σ s = M/Asz1=M/Ws
Определяем z1:

здесь  =0,55;
=0,55; 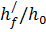 =3,8/22=0,173;
=3,8/22=0,173;  =19 см; по формуле находим
=19 см; по формуле находим  :
:

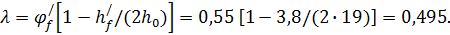
Значение δ от действия всей нормативной нагрузки:

то же, от действия постоянной и длительной нагрузки:


Вычисляем  при кратковременном действии всей нагрузки:
при кратковременном действии всей нагрузки:
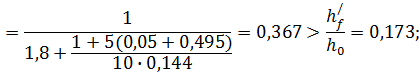
продолжаем расчет как тавровых сечений.
Значение z1 по формуле

Упругопластический момент сопротивления железобетонного таврового сечения после образования трещин
Ws=Asz1= 13,2·16,6=220 см2.
Расчет по длительному раскрытию трещин. Mld= 30,5 кН·м. Напряжение в растянутой арматуре при действии постоянных и длительных нагрузок

где Ws =220 см2 принято без пересчета величины z1 так как значение 
 δ ld =0,033 (вместо δ ld =0,05) изменяется мало.
δ ld =0,033 (вместо δ ld =0,05) изменяется мало.
Ширина раскрытия трещины от действия постоянной и длительной нагрузок при φ l =1,3.

условие удовлетворяется.
Расчет по кратковременному раскрытию трещин. Mn= 46 кН·м; Mld =30,5 кН·м; acrc определяем по формуле.
Напряжение в растянутой арматуре при совместном действии всех нормативных нагрузок.
σ s1=Mn/Ws= 46·105/220=21 000 Н/см2=210 МПа.
Пририащение напряжения от кратковременного увеличения нагрузки от длительного действующей до ее полной величины Δσs=σs1 – σs2 =210 – 139=71 МПа.
Соответствующее приращение ширины раскрытия трещин при φ l =1 по формуле будет:

Ширина раскрытия трещин при совместном действии всех нагрузок acrc =0,026+0,065=0,091 мм < acrc1,max =0,4 мм, т.е. условие удовлетворяется.
Значение acrc по формуле можно подсчитывать без предварительного вычисления напряжений Δσs, подставляя в формулу значения σs= M/Ws. В этом случае расчет значений acrc будет иметь следующий вид:



0,065<  =0,3 мм;
=0,3 мм;
acrc= acrc1- acrc2+ acrc3= 0,075-0,049+0,065=0,091≈0,1 мм < acrc1,max= 0,4 мм.
Проверка по раскрытию трещин, наклонных к продольной оси. Ширину раскрытия трещин, наклонных к продольной оси элемента и армированных поперечной арматурой, определяют из формулы по СНиП 2.03.01-84:

где  - угловой коэффициент, равный 1,0 при учете кратковременных нагрузок, включая постоянные и длительные нагрузки продолжительного действия, и 1,5 для тяжелого бетона естественной влажности при учете постоянных и длительных нагрузок продолжительного действия;
- угловой коэффициент, равный 1,0 при учете кратковременных нагрузок, включая постоянные и длительные нагрузки продолжительного действия, и 1,5 для тяжелого бетона естественной влажности при учете постоянных и длительных нагрузок продолжительного действия;  =1,4 – для гладкой проволочной арматуры; α= Es /Eb= 2,1·105/(3,25·104)=6,46;
=1,4 – для гладкой проволочной арматуры; α= Es /Eb= 2,1·105/(3,25·104)=6,46;  = Asw / (bs)=0,85/(31,2·10)=0,0027 (здесь Asw – площадь сечения поперечных стержней; в трех каркасах предусмотрено 3Ø6А-I, Asw= 3·0,283=0,85 см2.
= Asw / (bs)=0,85/(31,2·10)=0,0027 (здесь Asw – площадь сечения поперечных стержней; в трех каркасах предусмотрено 3Ø6А-I, Asw= 3·0,283=0,85 см2.
Напряжение в поперечных стержнях (хомутах)

где

здесь  c= 2 h0= 2·19=38 см;
c= 2 h0= 2·19=38 см;
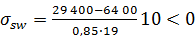 (получается отрицательная величина);
(получается отрицательная величина);
Qn= 29 400 Н – поперечная сила от действия полной нормативной нагрузки при γ f = 1,0; Qnld= 19 400 Н – то же, от постоянной и длительной нагрузок.
Так как 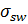 по расчету величина отрицательная, то раскрытия трещин, наклонных к продольной оси, не будет.
по расчету величина отрицательная, то раскрытия трещин, наклонных к продольной оси, не будет.
Проверка панели на монтажные нагрузки. Панель имеет четыре монтажные петли из стали класса А-I, расположенные на расстоянии 70 см от концов панели. с учетом коэффициента динамичности kd =1,4 расчетная нагрузка от собственного веса панели
q=kd · γf · g · b= 1,41,1·2750·1,19=5050 Н/м,
где q=hred ·ρ=0,11·25 000=2750 Н/м2 – собственный вес панели; b - конструктивная ширина панели; hred – приведенная толщина панели; ρ – плотность бетона.
Расчетная схема панели показана на рис. Отрицательный изгибающий момент консольной части панели
M=ql21/ =5050·0,72/2=1240 Н·м.
Этот момент воспринимается продольной монтажной арматурой каркасов. Полагая, что z1= 0,9 h0, требуемая площадь сечения указанной арматуры составляет

что значительно меньше принятой конструктивно арматуры 3Ø10А-II,  .
.
При подъеме панели вес ее может быть передан на две петли. Тогда усилие на одну петлю составляет
N=ql/2= 5050·6,37/2=16 100 Н.
Площадь сечения арматуры петли
As=N/Rs= 16 100/210(100)=0,765 см2;
принимаем конструктивно стержни диаметром 12 мм, As= 1,13 см2.
Не нашли, что искали? Воспользуйтесь поиском: