
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример расчета ребристой панели перекрытия
Требуется рассчитать и сконструировать ребристую панель для перекрытия производственного здания. Номинальные размеры панели в плане 6 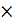 1,2 м. Действующие на перекрытие постоянные нагрузки принять по таблице 5.
1,2 м. Действующие на перекрытие постоянные нагрузки принять по таблице 5.
Таблица 5 – Нагрузка на междуэтажное перекрытие производственного здания
| Вид нагрузки | Нормативная нагрузка, Н/м2 | Коэффициент надежности по нагрузке | Расчетная нагрузка, Н/м2 |
| Постоянная: От плиточного пола, при t= 15 мм; ρ=2000 кг/м3 от цементного выравнивающего слоя, при t= 20 мм, ρ=2000 кг/м3 от шлакобетонных плит при t= 60 мм, ρ=1600 кг/м3 от железобетонной панели приведенной толщиной t= 100 мм, ρ=2500 кг/м3 | 1,1 1,3 1,2 1,1 | ||
| Итого Временная: кратковременная pcd длительная pld | 
| – 1,2 1,2 | 
|
| Итого Полная нагрузка | 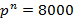

| – – | 

|
Временная нормативная нагрузка 7000 Н/м2, в том числе длительного действия 5000 Н/м2. Коэффициент надежности  . Ребра панели армируют сварными каркасами из стержневой стали класса А-III, плиту армируют сварной сеткой из проволоки класса Вр-I. Бетон панели класса В25.
. Ребра панели армируют сварными каркасами из стержневой стали класса А-III, плиту армируют сварной сеткой из проволоки класса Вр-I. Бетон панели класса В25.
Расчетные данные по табл. Для бетона класса В25: Rb= 14,5 МПа; Rbt =1,05 МПа, 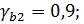 Rbser= 18,5 МПа; Rbt,ser= 1,6 МПа, Eb= 27
Rbser= 18,5 МПа; Rbt,ser= 1,6 МПа, Eb= 27  103 МПа; для арматуры класса А-III: Rs= 355 МПа (при диаметре 6
103 МПа; для арматуры класса А-III: Rs= 355 МПа (при диаметре 6  8 мм), Rsw= 290 МПа, Es =2
8 мм), Rsw= 290 МПа, Es =2  105 МПа; для арматуры диаметром 5 мм класса Вр-I: Rs =360 МПа; Rsw= 260 МПа и Es =1,7
105 МПа; для арматуры диаметром 5 мм класса Вр-I: Rs =360 МПа; Rsw= 260 МПа и Es =1,7  105 МПа.
105 МПа.
Определение нагрузок и усилий. Нагрузки на 1 м длины панели шириной 1,2 м: постоянная нормативная qn =4200·1,2=5100; постоянная расчетная q= 4800·1,2=5760; временная нормативная pn =8000·1,2=9600; расчетная p= 9600·1,2=11 500, в том числе временная длительная нормативная pnld= 5000·1,2=6000; временная длительная расчетная pld =5000·1,2·1,2=7200; кратковременная нормативная pncd =3000·1,2=3600; кратковременная расчетная pcd =3000·1,2·1,2=4320 Н/м.
Расчетная длина панели при ширине прогона b= 20 см:
l0=l-b/ 2=6-0,2/2=5,9 м.
Расчетная схема панели представляет собой свободно опертую балку таврового сечения с равномерно распределенной нагрузкой.
Определяем расчетные изгибающие моменты от полной расчетной нагрузки
M=ql20γn/ 8=(5760+11 500) ·5,92·0,95/8=71 500 Н·м = 71,5 кН·м;
от полной нормативной нагрузки
Mn =(5100+9600) ·5,92·0,95/8=61 000 Н·м;
от нормативной постоянной и длительной временной нагрузок
Mnld= (5100+6000) · 5,92·0,95/8=46 000 Н·м;
от нормативной кратковременной нагрузки
Mncd= 3600·5,92·0,95/8=14 900 Н·м.
Максимальная расчетная поперечная сила
Q= ql20γn/ 2=17,2·5,9·0,95/2=48,3 кН,
где q = 5760+11 500=17 260 Н/м=17,26 кН/м.
Предварительное определение сечения панели. Высоту сечения панели находим из условий обеспечения прочности и жесткости по эмпирической формуле

где 
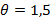 - для ребристой панели с полкой в сжатой зоне; с =30 – при применении арматуры из стали класса А-III;
- для ребристой панели с полкой в сжатой зоне; с =30 – при применении арматуры из стали класса А-III;
принимаем h= 40 см кратко 5 см.
Применительно к типовым заводским формам предварительно назначаем другие размеры сечения: толщину продольных ребер 80 и 100 мм (средняя толщина bp =90 мм), толщину плиты h/f= 60 мм, высоту поперечных ребер 200 мм, ширину сечения внизу 60 мм и вверху 110 мм.
Для расчета арматуры сечения ребристой панели приводим к тавровому с полкой в сжатой зоне: ширину сжатой полки b/f =116 мм, так как h/f/h =6/40=0,15>0,1 и имеются поперечные ребра; толщину h/f= 6 см, суммарную ширину приведенного ребра b= 2 bp =2·9=18 см. Рабочая высота сечения предварительно h0=h-a= 40-4=36 см.
Проверяем соблюдение условия, полагая предварительно, что коэффициент φω1=1:

48 300<0,3·1·0,87·14,5·0,9(100)18·36=221·103 Н,
где 
Условие соблюдается, принятое сечение достаточно для обеспечения прочности по наклонной полосе.
Расчет нормальных сечений по прочности. Устанавливаем расчетный случай для тавровых сечений, проверяя условие
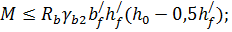
M=7 150 000 Н·см<14,5·0,9(100)116·6(36-0,5·6);
M= 71,5·105<300·105 Н·см.
Условие соблюдается, следовательно, нейтральная ось проходит в полке (x<h/f):

по таблице 6 находим 
Таблица 6 – Данные для расчета изгибаемых элементов прямоугольного сечения, армированных одиночной арматурой
| ᶓ=x/h0 | r0= 1/ 
| ɳ= zb/h0 | A0 | ᶓ=x/h0 | r0= 1/ 
| ɳ= zb/h0 | A0 |
| 0,01 | 0,995 | 0,01 | 0,36 | 1,84 | 0,82 | 0,295 | |
| 0,02 | 7,12 | 0,99 | 0,02 | 0,37 | 1,82 | 0,815 | 0,301 |
| 0,03 | 5,82 | 0,985 | 0,03 | 0,38 | 1,8 | 0,81 | 0,309 |
| 0,04 | 5,05 | 0,98 | 0,039 | 0,39 | 1,78 | 0,805 | 0,314 |
| 0,05 | 4,53 | 0,975 | 0,048 | 0,40 | 1,77 | 0,8 | 0,32 |
| 0,06 | 4,15 | 0,97 | 0,058 | 0,41 | 1,75 | 0,795 | 0,326 |
| 0,07 | 3,85 | 0,965 | 0,067 | 0,42 | 1,74 | 0,79 | 0,332 |
| 0,08 | 3,31 | 0,96 | 0,077 | 0,43 | 1,72 | 0,785 | 0,337 |
| 0,09 | 3,41 | 0,955 | 0,085 | 0,44 | 1,69 | 0,78 | 0,343 |
| 0,10 | 3,24 | 0,95 | 0,095 | 0,45 | 1,68 | 0,775 | 0,349 |
| 0,11 | 3,11 | 0,945 | 0,104 | 0,46 | 1,67 | 0,77 | 0,354 |
| 0,12 | 2,98 | 0,94 | 0,113 | 0,47 | 1,66 | 0,765 | 0,359 |
| 0,13 | 2,88 | 0,935 | 0,121 | 0,48 | 1,64 | 0,76 | 0,365 |
| 0,14 | 2,77 | 0,93 | 0,13 | 0,49 | 1,63 | 0,755 | 0,37 |
| 0,15 | 2,68 | 0,925 | 0,139 | 0,50 | 1,62 | 0,75 | 0,375 |
| 0,16 | 2,61 | 0,92 | 0,147 | 0,51 | 1,61 | 0,745 | 0,38 |
| 0,17 | 2,53 | 0,915 | 0,155 | 0,52 | 1,6 | 0,74 | 0,385 |
| 0,18 | 2,47 | 0,91 | 0,164 | 0,53 | 1,59 | 0,735 | 0,39 |
| 0,19 | 2,41 | 0,905 | 0,172 | 0,54 | 1,58 | 0,73 | 0,394 |
| 0,20 | 2,36 | 0,90 | 0,18 | 0,55 | 1,57 | 0,725 | 0,399 |
| 0,21 | 2,31 | 0,895 | 0,188 | 0,56 | 1,56 | 0,72 | 0,403 |
| 0,22 | 2,26 | 0,89 | 0,196 | 0,57 | 1,55 | 0,715 | 0,408 |
| 0,23 | 2,22 | 0,885 | 0,203 | 0,58 | 1,54 | 0,71 | 0,412 |
| 0,24 | 2,18 | 0,88 | 0,211 | 0,59 | 1,535 | 0,705 | 0,416 |
| 0,25 | 2,14 | 0,875 | 0,219 | 0,60 | 1,53 | 0,7 | 0,42 |
| 0,26 | 2,1 | 0,87 | 0,226 | 0,61 | 1,525 | 0,695 | 0,424 |
| 0,27 | 2,07 | 0,865 | 0,236 | 0,62 | 1,52 | 0,69 | 0,428 |
| 0,28 | 2,04 | 0,86 | 0,241 | 0,63 | 1,515 | 0,685 | 0,432 |
| 0,29 | 2,01 | 0,855 | 0,248 | 0,64 | 1,51 | 0,68 | 0,435 |
| 0,30 | 1,98 | 0,85 | 0,255 | 0,65 | 1,5 | 0,675 | 0,439 |
| 0,31 | 1,95 | 0,845 | 0,262 | 0,66 | 1,495 | 0,67 | 0,442 |
| 0,32 | 1,93 | 0,84 | 0,269 | 0,67 | 1,49 | 0,665 | 0,446 |
| 0,33 | 1,9 | 0,835 | 0,275 | 0,68 | 1,485 | 0,66 | 0,449 |
| 0,34 | 1,88 | 0,83 | 0,282 | 0,69 | 1,48 | 0,655 | 0,452 |
Проверяем условие  находим значение
находим значение  :
:

где 
 условие удовлетворяется;
условие удовлетворяется;
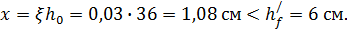
Площадь сечения продольной арматуры в ребрах

принято 4 Ø 14 А-III, AS= 6,16 см2, располагая по два стержня в ребре (можно также предусмотреть 2 Ø 20 А-III, AS= 6,28 см2, по одному продольному стержню в каждом ребре). В данном примере принято 2 Ø 14 А-III в каждом ребре, чтобы показать обрыв части продольных стержней в пролете в соответствии с эпюрой изгибающего момента; этим можно сократить расход арматуры. При двухрядном расположении арматуры h0=h-a3-d1-a1/ 2=40-2-1,4—2,5/2=35,3 см  35 см (здесь a3
35 см (здесь a3  2 см и a1
2 см и a1  2,5 см – соответственно защитный слой бетона и расстояние между стержнями, см).
2,5 см – соответственно защитный слой бетона и расстояние между стержнями, см).
Расчет наклонного сечения по прочности. Q= 48,3 кН. Вычисляем проекцию расчетного наклонного сечения на продольную ось с. Влияние свесов сжатых полок (при двух ребрах):

Коэффициент φ n =0, ввиду отсутствия предварительного обжатия. Вычисляем сумму коэффициентов (1+φ f +φ n)=1+0,25+0=1,25<1,5. Параметр Bb= φ b2 ·(1+ φ f + φ n)· Rbtγb2bh20= 2·1,25·1,05(100)0,9·18·362=55,3·105 Н·см.
В расчетном наклонном сечении Qb=Qsw=Q/ 2, поэтому наклонное сечение c=Bb/ 0,5 Q= 55,3·105/0,5·48 300=230 см>2 h0= 2·36=72 см; принимаем c= 2 h0= 72 см. Тогда поперечное усилие Qb = Bb/c =55,3·105/72=75,7·103 Н=75,7 кН, что больше Q= 48,3 кН, следовательно, поперечная арматура по расчету не требуется.
Принимаем конструктивно поперечные стержни Ø 6 А-I, Asw =0,283 см2. Шаг поперечных стержней 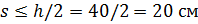 и не более s= 15 см.
и не более s= 15 см.
Принимаем на приопорном участке длиной ¼ пролета (600/4=150 см) шаг поперечных стержней s= 15·см, а в средней половине пролета панели проектируем их размещение по конструктивным требованиям при  и не более s= 50 см. Принимаем в средней половине длины каркасов продольных ребер шаг поперечных стержней s2 =30 см.
и не более s= 50 см. Принимаем в средней половине длины каркасов продольных ребер шаг поперечных стержней s2 =30 см.
Определение места обрыва в пролете продольных стержней. В пролете допускается обрывать не более 50% расчетной площади сечения стержней, вычисленных по максимальному изгибающему моменту. При этом в каждом плоском сварном каркасе не менее одного продольного стержня должно быть заведено за грань опоры.
За грань опоры заводят по одному стержню диаметром 14 мм в каждом каркасе К-I, всего As1 =2·1,54=3,08 см2. Высота сжатой зоны сечения

Момент воспринимаемый сечением с арматурой 2Ø14А-III,
My=RsAs1zb= 365(100)3,08·34,6=3 890 000 Н·м=38,9 кН·м,
где zb=h0 – 0,5 x =35 – 0,5·0,75=34,6 см.
Определяем место теоретического обрыва продольной арматуры из условия:
My=Qy – 0,5 qy2= 0,5 ql0y – 0,5 qy2;
38,9=48,3 y – 0,5·17,26 y2;
8,63 y2 – 48,3 y+ 38,9=0;

y1= 0,96 м, y2 =4,62 м.
Обрываемые стержни заводят за грань теоретического обрыва на длину ω, согласно эпюре изгибающих моментов. Значение ω по нормам принимают равным большему из двух следующих значений:

где Qy=Q (1-2 y1/l0)=48,3(1-2·0,96/5,9)=32,5 кН – из подобия треугольников эпюры поперечных сил Qs,inc= 0, ввиду отсутствия отогнутой арматуры;
по формуле определяем:
qsw=RswAsw / s= 175·0,283(100)/15=662 Н/см;


принимаем ω=32 см.
Расчет плиты панели. Плита (полка) панели является трехпролетной неразрезной, опертой по контуру на продольные и поперечные ребра. Отношение длинной стороны l2 и короткой l1 в чистоте между ребрами:
l2/l1= (1790-110)/(1160-2·100)=1,75<2.
Определение нагрузок и усилий. Собственный вес конструкции пола по табл. 3.4: нормативный 300+1000+400=1700 Н/м2; расчетный 330+1200+520=2050 Н/м2.
Собственный вес плиты: нормативный 0,06·25 000=1500 Н/м2; расчетный 1500·1,1=1650 Н/м2.
Суммарная равномерно распределенная нагрузка: полная нормативная (gn+pn)=1700+1500+8000=11200Н/м2; полная расчетная (g+p)=2050+1650+9600=13 300 Н/м2; нормативная постоянная и длительная временная (gnld+pnld)=1700+1500+5000=8200 Н/м2.
Вычисляем изгибающие моменты методом предельного равновесия. Моменты в среднем поле неразрезной плиты при l2/l1= 1,5  2 можно принять:
2 можно принять:
 ;
;

Из основного уравнения равновесия плит

принимая коэффициент 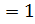 , которым учитывается влияние распора в зависимости от жесткости окаймляющих ребер и отношения l2/l1, для принятых соотношений моментов находим момент M1 на полосу шириной 1 м в направлении короткой стороны (при γ n =0,95):
, которым учитывается влияние распора в зависимости от жесткости окаймляющих ребер и отношения l2/l1, для принятых соотношений моментов находим момент M1 на полосу шириной 1 м в направлении короткой стороны (при γ n =0,95):

то же, в направлении длинной стороны:


Крайние поля неразрезной плиты как окаймленные со всех сторон ребрами рассматриваются аналогично среднему полю, и так как отношения сторон в них по чти равны l2/l1 среднего поля, то изгибающие моменты принимаем по среднему полю.
Определяем площадь сечения арматуры на 1 м плиты в направлении короткой стороны при h0=h-a= 6 – 1,5=4,5 см:

где 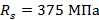 - для арматуры класса Вр-I диаметром 3 мм. Принимаем рулонную сетку 5 из проволоки класса Вр-I диаметром 3 мм шириной 1100 мм с поперечной рабочей арматурой
- для арматуры класса Вр-I диаметром 3 мм. Принимаем рулонную сетку 5 из проволоки класса Вр-I диаметром 3 мм шириной 1100 мм с поперечной рабочей арматурой  см2 при шаге s= 200 мм; сетка раскатывается вдоль длинной стороны с отгибом на опорах в верхнюю зону.
см2 при шаге s= 200 мм; сетка раскатывается вдоль длинной стороны с отгибом на опорах в верхнюю зону.
В направлении длинной стороны As2= 0,5 As1= 0,158 см2; из конструктивных соображений принято As2=As1= 0,36 см2.
Для восприятия опорных моментов  (по длинной стороне), величина которых равна M1, укладываем конструктивно сетки 3 шириной 500 мм из Ø3 Вр-I с перегибом на продольном ребре. Поперечные стержни сеток 3 перепускают в плиту на длину 0,2 l1= 200 мм.
(по длинной стороне), величина которых равна M1, укладываем конструктивно сетки 3 шириной 500 мм из Ø3 Вр-I с перегибом на продольном ребре. Поперечные стержни сеток 3 перепускают в плиту на длину 0,2 l1= 200 мм.
Расчет поперечного ребра панели. Определение нагрузок и усилий. Максимальная нагрузка на среднее поперечное ребро передается с треугольных грузовых площадей Ac= 0,5 l21. Расчетная схема поперечного ребра представляет собой балку с защемленными опорами, нагруженную треугольной нагрузкой с максимальной ординатой q1 и собственным весом qc. Треугольную нагрузку допускается заменить на эквивалентную равномерно распределенную по формуле qe= 5/8 q1.
q1= (g+p)(l1+bp)=13 300(0,96+0,085)=13 900 Н/м,
где bp= (11+6)/2=8,5 см – средняя толщина поперечного ребра;
qc=bp (hp – h/f) ργf =0,085(0,2-0,06)25 000·1,1=330 Н/м,
Суммарная равномерно распределенная нагрузка
q=qe+qc= (5/8)13 900+330=9030 Н/м.
С учетом развития пластических деформаций изгибающие моменты в пролете Mc и на опоре  можно определять по равномоментной схеме (Mc=
можно определять по равномоментной схеме (Mc=  =M):
=M):
M=ql21/ 16=9030·0,962/16=520 Н·м.
Расчет продольной арматуры. В пролете поперечное ребро имеет тавровое сечение с полкой в сжатой зоне. Расчетная ширина полки b/f=bp+ 2 l1/ 6=8,5+2·96/6=49 см и b/f= bp+ 12 h/f= 8,5+12·6=80,5 см; принимаем меньшее значение b/f= 40 см; высота ребра h =20 см и рабочая высота h0=h-a= 20 – 2,5=17,5 см
A0=M/b/f h20Rbγb2 =52 000/40·17,52·14,5(100)0,9=0,00325,
что меньше минимального значения A0, по табл.2.12 принимаем 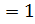 :
:
As=M/ɳ0Rs= 52 000/17,5·225(100)=0,132 см2;
принимаем из конструктивных соображений Ø6 А-I, As= 0,28 см2; арматуру в верхней зоне и поперечные стержни также принимаем из арматуры Ø6 мм; шаг поперечных стержней 150 мм. Из арматуры Ø6 А-I выполняют каркас 2 в крайних поперечных ребрах.
Расчет панели по деформациям (прогибам). Изгибающий момент в середине пролета равен: от полной нормативной нагрузки Mn =61 кН·м; от нормативной постоянной и длительной временной нагрузок Mnld =46 кН·м и от кратковременной нагрузки Mncd= 14, 9 кН·м.
Определяем геометрические характеристики приведенного сечения панели:
α= Es /Eb= 2 ·105/0,27·105=7,4;

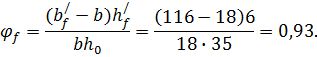
Вычисление прогиба панели приближенным методом. Проверяем условие, определяющее необходимость вычисления прогибов при l/h0= 590/35=17>10:
l/h0  λlim,
λlim,
по табл.2.20 при μα=0,072 и арматуре из стали класса А-III находим λlim= 18,5/(1/200)/(2,5/590)=15,5 (здесь выражение в скобках учитывает разницу в прогибе 1/200 и 2,5 см= l/ 236)
590/35=17> λlim= 15,5,
т.е. расчет прогибов требуется.
Прогиб в середине пролета панели по формуле
ftot=Sl2·1/rc= 5/48·5902(1/ rc),
где 1/ rc – кривизна в середине панели при учете постоянных и длительных нагрузок равна

здесь коэффициенты  =0,48 и
=0,48 и  =0,125 приняты по табл.2.19 в зависимости от μα=0,072≈0,07 и φf(γ)=0,93 (по интерполяции) для тавровых сечений с полкой в сжатой зоне; ftot= 5/48·5902·10-5=2,2 см<
=0,125 приняты по табл.2.19 в зависимости от μα=0,072≈0,07 и φf(γ)=0,93 (по интерполяции) для тавровых сечений с полкой в сжатой зоне; ftot= 5/48·5902·10-5=2,2 см<  =2,5 см – для ребристых перекрытий по эстетическим требованиям (таблица 7)
=2,5 см – для ребристых перекрытий по эстетическим требованиям (таблица 7)
Таблица 7 – Значения коэффициентов k1, k2 и k3
| γ/ | γ | Обозначение коэффициента | Значения коэффициентов при μα | |||||||
| 0,04 | 0,07 | 0,1 | 0,15 | 0,2 | 0,3 | 0,4 | 0,5 | |||
| k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,56 0,36 0,14 0,1 1,05 0,95 | 0,5 0,3 0,09 0,07 0,98 0,85 | 0,46 0,26 0,09 0,04 0,93 0,77 | 0,41 0,22 0,02 0,9 0,7 | 0,37 0,19 0,02 0,8 0,6 | 0,32 0,14 - - | 0,28 0,12 - - | 0,25 0,1 - - | ||
| 0,2 | k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,63 0,44 0,11 0,09 1,09 0,97 | 0,58 0,39 0,11 0,09 1,05 0,86 | 0,56 0,35 0,11 0,05 0,98 0,78 | 0,57 0,28 0,03 0,05 0,93 0,71 | 0,46 0,25 0,03 0,87 0,64 | 0,4 0,19 0,03 0,75 0,54 | 0,35 0,16 - - | 0,31 0,13 - - | |
| 0,6 | k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,69 0,49 0,21 0,11 1,16 1,05 | 0,64 0,46 0,21 0,11 1,05 0,87 | 0,63 0,43 0,16 0,08 0,99 0,79 | 0,61 0,39 0,16 0,08 0,93 0,71 | 0,58 0,35 0,05 0,88 0,65 | 0,52 0,28 0,05 0,8 0,55 | 0,46 0,23 0,76 0,51 | 0,42 0,2 0,69 0,46 | |
| k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,71 0,52 0,24 0,13 1,16 1,06 | 0,67 0,49 0,24 0,13 1,05 0,89 | 0,66 0,47 0,18 0,1 0,82 | 0,65 0,44 0,18 0,1 0,94 0,74 | 0,63 0,41 0,07 0,06 0,9 0,68 | 0,59 0,35 0,07 0,06 0,83 0,59 | 0,54 0,3 0,77 0,52 | 0,5 0,26 0,76 0,49 | ||
| 0,2 | k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,56 0,36 0,23 0,12 1,16 1,09 | 0,49 0,3 0,23 0,12 1,09 0,94 | 0,44 0,26 0,16 0,08 1,02 0,85 | 0,4 0,22 0,16 0,08 0,97 0,77 | 0,37 0,19 0,07 0,03 0,83 0,66 | 0,32 0,14 0,07 0,03 - - | 0,28 0,11 - - | 0,25 0,1 - - | |
| 0,6 | k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,59 0,37 0,39 0,19 1,21 1,17 | 0,49 0,3 0,39 0,19 1,13 1,02 | 0,44 0,25 0,32 0,17 1,09 0,92 | 0,4 0,21 0,32 0,17 0,82 | 0,37 0,18 0,2 0,09 0,84 0,7 | 0,32 0,14 0,2 0,09 - - | 0,28 0,11 0,08 0,03 - - | 0,25 0,1 0,08 0,03 - - | |
| k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,84 0,4 0,46 0,24 - - | 0,49 0,29 0,46 0,24 1,24 1,12 | 0,44 0,24 0,44 0,23 1,09 | 0,4 0,2 0,44 0,23 0,85 | 0,37 0,17 0,29 0,14 - - | 0,32 0,14 0,29 0,14 - - | 0,28 0,11 0,15 0,06 - - | 0,25 0,1 0,15 0,06 - - | ||
| 0,2 | 0,2 | k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,63 0,43 0,24 0,13 1,21 1,1 | 0,58 0,37 0,24 0,13 1,07 0,89 | 0,55 0,34 0,17 0,08 1,02 0,81 | 0,5 0,28 0,17 0,08 0,97 0,73 | 0,46 0,24 0,08 0,04 0,9 0,67 | 0,39 0,19 0,08 0,04 0,77 0,56 | 0,35 0,16 - - | 0,31 0,13 - - |
| Продолжение | ||||||||||
| 0,6 | 0,6 | k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | 0,76 0,53 0,46 0,22 - - | 0,65 0,46 0,46 0,22 1,16 | 0,61 0,41 0,44 0,2 1,05 0,87 | 0,57 0,38 0,44 0,2 0,99 0,76 | 0,55 0,34 0,28 0,12 0,96 0,69 | 0,5 0,28 0,28 0,12 0,86 0,6 | 0,45 0,23 0,11 0,04 0,8 0,54 | 0,41 0,2 0,11 0,04 0,72 0,48 |
| k 1 cd k 1 ld k 2 cd k 2 ld k 3 cd k 3 ld | - - 0,72 0,26 - - | 0,71 0,5 0,72 0,26 - - | 0,66 0,45 0,7 0,25 1,12 0,98 | 0,61 0,4 0,7 0,25 1,03 0,83 | 0,58 0,38 0,55 0,2 0,98 0,75 | 0,56 0,34 0,55 0,2 0,93 0,65 | 0,52 0,29 0,31 0,12 0,86 0,58 | 0,48 0,26 0,31 0,12 0,83 0,54 |
Определение прогиба по точным формулам. Вначале проверяют условие Mr  Mcrc, при соблюдении которого нормальные трещины в наиболее нагруженном сечении по середине пролета не образуются. Момент от полной нормативной нагрузки Mn =61 кН·м. Момент трещинообразования Mcrc вычисляют по формуле, принимая Mrp= 0:
Mcrc, при соблюдении которого нормальные трещины в наиболее нагруженном сечении по середине пролета не образуются. Момент от полной нормативной нагрузки Mn =61 кН·м. Момент трещинообразования Mcrc вычисляют по формуле, принимая Mrp= 0:
Mcrc=Rbt,serWpl, где Wpl=γWred.
По прил. VI для тавровых сечений с полкой в сжатой зоне γ= 1,75, а упругий момент сопротивления сечения для растянутой грани сечения
Wred=Ired /y0; y0=Sred /Ared.
Для вычисления Ired и y0 определяем площадь приведенного сечения:
Ared=A+αAs= 116·6+18·34+6,16·7,4·5=1354 см2.
Статический момент площади приведенного сечения относительно нижней грани ребра:
Sred=S0+αSs= 116·6·37+18·34·17+6,16·7,4·5=36 470 см3.
Расстояние от центра тяжести площади приведенного сечения до нижней грани ребра:
y0= Sred /Ared= 36 470/1354=27 см;
h – y0= 40 – 27=13 см.
Момент инерции приведенного сечения относительно центра тяжести сечения
Ired=I+αAsy2s= 116·63/12+116·102+18·343/12+18·34·102+7,4·6,16·222=
=206 300 см4;
где ys=y0-a= 27 – 5=22 см; в формуле слагаемые с Asp, A/sp и A/s исключены, так как As= 0; A/sp= 0, а A/s не учтены ввиду малости.
Момент сопротивления:
Wred=Ired /yo= 206 300/ 27=7650 см3;
Wpl=γWred= 1,75·7650=13 400 см3.
Момент трещинообразования
Mcrc=Rbt,serWpl= 1,6(100)13 400=21,4·105 Н·см=21,4 кН·м,
что меньше Mn= 61 кН·м, следовательно, трещины в растянутой зоне сечения по середине пролета образуются. Необходимо выполнять расчет прогибов с учетом образования трещин в растянутой зоне. Кроме того, требуется проверка по раскрытию трещин.
Полная кривизна 1/ r для участка с трещинами по формуле:
1/ r= 1/ r1 – 1/ r2+ 1/ r3
и соответственно полный прогиб панели ftot=f1 – f2+f3, где f1 – прогиб от кратковременного действия всей нагрузки; f2 – то же, от действия только постоянных и длительных нагрузок; f3 – прогиб от длительного действия постоянных и длительных нагрузок.
Вычисление f1. Для середины пролета панели Mr = Mn =61 кН·м. Для определения кривизны дополнительно вычислим:
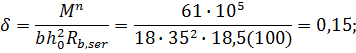

Относительная высота сжатой зоны в сечении с трещиной по

что меньше h/f /h0 =6/35=0,172 и меньше 2 a/ /h0 =5/35=0,143; сечения рассчитывают как прямоугольные шириной b/f =116 см; принимаем без учета арматуры As/ в формулах для определения λ, φ f и z1 значение h/f = 0:

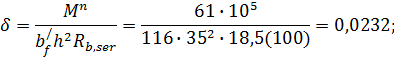

Плечо внутренней пары сил по формуле при 

Определяем коэффициент ψ s по формуле:
ψ s= 1,25 – φ lsφm= 1,25 – 1,1·0,35=0,87<1,
где
φm=Rbt,serWpl /Mn= 1,6(100)(13 400 /61·105)=0,35;
φ ls= 1,1
Кривизна 1/ r1 в середине пролета панели при кратковременном действии всей нагрузки по формуле и ψ b= 0,9; ν=0,45:

Прогиб f1 по формуле

Вычисление f2 · Mld =46 кН·м. Заменяющий момент Mr=Mld= 46 46 кН·м:


по данным расчета f1 принимаем:
ψ s= 0,87; ψ b =0,9; ν=0,45;

Прогиб f2

Вычисление f3. Кривизну 1/ r3 при длительном действии постоянной и длительной нагрузок определяем с использованием данных расчета кривизны 1/ r1 и 1/ r2: Mr=Mld= 46 кН 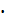 м;
м;  0,087; z1 =33,5 см; φ m =0,35. Коэффициент ν=0,15.
0,087; z1 =33,5 см; φ m =0,35. Коэффициент ν=0,15.
Коэффициент ψ s при φ ls =0,8: ψ s= 1,25 – φ ls φ m= 1,25-0,8·0,35=0,97<1.
Кривизна 1/ r3 в середине пролета панели

Прогиб f3

Суммарный прогиб ftot=f1 – f2+f3= 1,76-1,31+2,05=2,5 см <  =1/150 l=
=1/150 l=
= 3,9 см по конструктивным требованиям и flim =2,5 см – по эстетическим требованиям.
Расчет панели по раскрытию трещин, нормальных к продольной оси. Согласно данным табл.2.9, ребристая панель перекрытия относится к третьей категории трещиностойкости. Предельно допустимая ширина раскрытия трещин составляет acrc1= 0,4 мм и acrc2 =0,3 мм.
По формуле ширина раскрытия трещин

где  =1;
=1;  =1;
=1;  =(1,5 – 15
=(1,5 – 15  );
);  =1; δa=1 (так как a2= 3 см < 0,2 h= 0,2·40=8 см); d= 14 мм;
=1; δa=1 (так как a2= 3 см < 0,2 h= 0,2·40=8 см); d= 14 мм;  = As /bh0= 6,16/18·35=0,0098<0,02.
= As /bh0= 6,16/18·35=0,0098<0,02.
Расчет по длительному раскрытию трещин. Ширину длительного раскрытия трещин определяют от длительного действия постоянных и длительных нагрузок. Изгибающий момент в середине пролета панели Mld =46 кН·м. Напряжение в растянутой арматуре

Так как растянутая арматура в ребрах расположена в два ряда, то напряжение σ s необходимо умножить на поправочный коэффициент δ n (по СНиП 2.03.01 – 84).
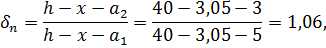
где x=  h0 =0,087·35=3,05 см; a2= 3 см – расстояние от нижней грани сечения до центра тяжести нижнего ряда продольной арматуры; a1 =5 см – уточненное расстояние от нижней грани сечения до центра тяжести всей растянутой арматуры As.
h0 =0,087·35=3,05 см; a2= 3 см – расстояние от нижней грани сечения до центра тяжести нижнего ряда продольной арматуры; a1 =5 см – уточненное расстояние от нижней грани сечения до центра тяжести всей растянутой арматуры As.
При длительном действии нагрузок принимаем φ l =1,6 – 15μ=1,6 – 15·0,0098=1,453. Коэффициент:
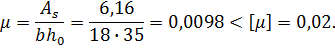

Расчет по кратковременному раскрытию трещин. Ширину кратковременного раскрытия трещин определяют как сумму ширины раскрытия от длительного действия постоянных и длительных нагрузок acrc3 и приращения ширины раскрытия от действия кратковременных нагрузок (acrc1 – acrc2):
acrc= (acrc1 – acrc2)+ acrc3,
где acrc3= 0,2 мм.
Напряжение в растянутой арматуре при кратковременном действии всех нормативных нагрузок

Напряжение в растянутой арматуре от действия постоянных и длительных нагрузок

Приращение напряжения при кратковременном увеличении нагрузки от длительно действующей до ее полной величины составляет
Δσ s=σs1 – σs2 =296-223=73 МПа
Приращение ширины раскрытия трещин при φ l =1 по формуле

Суммарная ширина раскрытия трещин
acrc,tot= 0,2+0,046=0,25 мм <  =0,4 мм.
=0,4 мм.
Затем выполняют расчет панели по раскрытию наклонных трещин, а также расчет панели в стадии изготовления, транспортирования и монтажа.
Не нашли, что искали? Воспользуйтесь поиском: