ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Огибающая и фаза узкополосного случайного процесса.
Случайный процесс y(t) = Um(t) cos (w0t+j(t)) называется узкополосным, если его ширина спектра значительно меньше, чем средняя частота w0.
Um(t) - огибающая случайного процесса (случайная амплитуда) на рис.11.9;
j(t) - фаза случайного процесса.
Для нормального случайного процесса фаза j(t) распределена равномерно (см. выше).
u(t) Um(t)
Рис.11.9.
 |
t
 |
Огибающая нормального случайного процесса Um(t) распределена по закону Релея:
; Um ³ 0
W(Um)
 |
з-н Релея
з-н Райса Рис.11.10.
 |
0 Um
Если узкополосный случайный процесс есть сумма нормального шума и гармонического колебания с амплитудой А, то его огибающая распределена по обобщенному закону Релея (закон Райса):
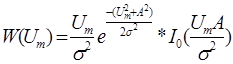закон Райса.
I0(.) - функция Бесселя от мнимого аргумента.
11.6.ФПВ и ФРВ для дискретных случайных процессов.
Дискретные случайные процессы принимают с определенной вероятностью значения, отличающиеся одно от другого на конечную величину. Вероятность таких значений – число не равное 0.
Рассмотрим реализацию дискретного случайного процесса.
x(t)
а
T1
Т2 t Рис.11.11
b
T 1+T2=T
Для эргодического стационарного случайного процесса усреднение по множеству реализаций эквивалентно усреднению по времени одной реализации.
T1/T - вероятность того, что случайный процесс принимает
значение а.
T2/T - вероятность того, что случайный процесс принимает
значение b.
 |
ФПВ заданного случайного процесса в соответствии с полученным выражением показана на рис.11.12:
 |
W(x)
Рис.11.12. 
b 0 a x
ФРВ для случайного процесса принимающего 2 значения x=a и x=b имеет вид:
F(x)
1
T2/T1
Рис.11.13.
t
b a
Вычислим среднее значение двоичного дискретного случайного процесса, принимающего 2 значения:
x=a c вероятностью T1/T, x=b c вероятностью T2/T 
11.7.Нелинейные безынерционные преобразования случайного процесса.
Нелинейное преобразование:
y(t)=f[x(t)] – называется безынерционным, если y(tk) в момент времени tk зависит только от x(tk).
ФПВ для процесса y на выходе:
Пусть характеристика нелинейного элемента может быть аппроксимирована линейно-ломаными.
y
Рис.11.14
b
-a a x
-b
Это нелинейное устройство называется ограничителем.
Пусть на входе ограничителя действует нормальный случайный процесс с нулевым средним m1x=0.
ФПВ процесса x нарисована на рис.11.15 (верхний рисунок).
Рассчитаем ФПВ процесса y:
1. Пусть 
у=kx (k>1)
Подставим в W(x) вместо x, y/k, тогда
На интервале 
ФПВ для у будет нормальной, со средним значением m1y=0, но дисперсия y, т.е. 
.
W(x)
 |
x
-a a
 |
W(y)
Рис.11.15.
 |  |
-ka 0 ka y
2. Пусть:
Выражаем x через у, т.е. 
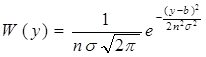
Это нормальная ФПВ со средним значением b и дисперсией 
3.Пусть:
Это нормальная ФПВ, m1= -b и дисперсия 
.
ФПВ процесса y дана на рис.11.15 (нижний рисунок).
Не нашли, что искали? Воспользуйтесь поиском: