Влияние произвольных распределений отказов и восстановлений на нестационарные показатели надежности

Практические задачи, возникающие в теории надежности, по­казывают важность расчета и анализа нестационарных характери­стик, которые часто не принимаются во внимание, хотя продолжительность переходного процесса может быть довольно большой. Более того, существуют системы, стационарное состояние которых вообще не наступает.

Если f(t) и g(t) - плотности распределения времени безотказной работы и времени восстановления элемента, то функция готовности удовлетворяет следующему уравнению:

(4.3)

где функция w_в находится из уравнения

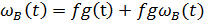(4.4)

Численное решение этих уравнений для многих распределений не представляет затруднений. Однако могут быть получены аналитические выражения функции готовности для некоторых часто встречающихся распределений. Функция готовности в терминах преобразования Лапласа имеет вид

(4.5)

Если законы распределения - экспоненциальные с параметрами λ и μ соответственно, то функция (4.5) дает формулу

(4.6)

Для случая, когда закон распределения времени безотказной работы экспоненциальный, а времени восстановления - неэкспоненциальный, можно рассмотреть для примера два распределения времени восстановления: равномерный и Эрланга 2-го порядка - с одинаковыми математическими ожиданиями и дисперсиями. Для равномерного распределения с параметрами а и Ь из формулы (4.5) следует

(4.7)

и в явном виде найти функцию готовности не удается. Для распре­деления Эрланга с параметром и. из формулы (4.5) следует

(4.8)

и функция готовности находится в явном виде

(4.9)

Точки экстремума получаются в результате решения уравнения , откуда 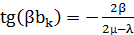Тем самым , k = 1,2,..., и функция АК_Г(t) имеет бесконечное число точек экстремума, а это соответствует колебательному процессу. Для значения 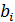, имеем

(4.10)

то есть 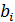, - точка минимума, в которой график функции готовно­сти лежит ниже стационарного значения К_Г Значения а_к, в кото­рых график функции

готовности пересекает линию K_Г(t) - К_Г, определяются

из уравнения . Это доказывает, что для произвольных распределений могут наблюдаться провалы функции готовности ниже ее стационарного значения [ ].

В отличие от экспоненциального случая, когда функция готовности всегда является монотонно убывающей, в общем случае это не имеет место, и очень часто у функции готовности наблюда­ются колебания. Поэтому может оказаться, что готовность системы для небольшого времени эксплуатации меньше, чем при ее дли тельной эксплуатации. С уменьшением дисперсии времени безотказной работы элементов усиливается колебательный характер функции K_Г(t) и значительно увеличивается время наступления стационарного режима системы.

В случае, если законы распределения - вырожденные со средними Т и Т_в соответственно, тогда из формулы (4.5) следует

Это выражение показывает, что функция K_r(t) тождественно равна единице на интервалах [k(Т + Т_в, k(Т + Т_в) + Т] и равна нулю вне этих интервалов (k = 0,1,2,...).

(4.12)

Стационарный режим здесь отсутствует, а коэффициент готовности не существует.

Не нашли, что искали? Воспользуйтесь поиском: