
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Пример выполнения задачи 1
На рисунке 1.51 изображена схема электрической цепи, параметры которой:
R1 = 10 Ом, R2 = 8 Ом, R3 = 2 Ом, R4 = 4 Ом, R5 = 9 Ом, R6 = 12 Ом,
Е2 = 15 В, R02 = 0,5 Ом, Е3 = 3 В, R03 = 0,8 Ом.
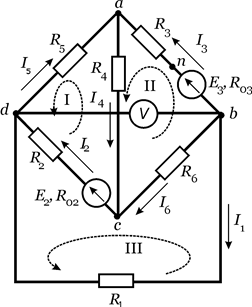
Рисунок 1.51
1. Составим на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.
Первый закон Кирхгофа: Алгебраическая сумма токов ветвей, сходящихся в любом узле электрической схемы, равна нулю.
Второй закон Кирхгофа: Алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура.
Решение:
1.1. Задаемся произвольно направлениями токов и обозначаем их на схеме. Пронумеровываем узлы схемы. Узел – это место соединения трех и более ветвей. В схеме на рисунке 1.51 четыре узла - a, b, c, d. По первому закону Кирхгофа составляем (y-1) = 3 уравнений, где у – количество узлов. Принято считать положительными токи, направленные к узлу.
1.2 По второму закону Кирхгофа количество уравнений определяется как: в-(у-1), где в – количество ветвей с неизвестными токами. В схеме на рисунке 1.51 всего шесть ветвей, следовательно, количество уравнений, необходимым для составления по второму закону Кирхгофа, равно 3:
6 – (4 – 1) = 3.
Выбираем независимые контуры и направление их обхода. Падения напряжений на резисторах берем со знаком «плюс», если направление обхода контура совпадает с направлением тока через этот резистр и со знаком «минус», если не совпадает.
1.3. Система уравнений, составленная по законам Кирхгофа, для электрической схемы на рисунке 1.51 имеет вид:



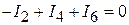
 (1)
(1)


Решение системы уравнений в системе MathCad показано на рисунке 1.52.

Рисунок 1.52
Не нашли, что искали? Воспользуйтесь поиском: