
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Оборудование: полупроводниковый резистор, нагреватель, электронный блок измерения температуры и сопротивления.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Полупроводники – это кристаллические тела, которые по электропроводности занимают промежуточное положение между металлическими проводниками и изоляторами. Но принципиальным отличием полупроводников от металлов является быстрое уменьшения сопротивления с ростом температуры, в то время как у металлов оно медленно растет. Также электропроводность полупроводников сильно зависит от примесей.
Полупроводники – это, как правило, кристаллы элементов 4-й группы таблицы Менделеева, например германия, кремния. При образовании кристалла между атомами возникает химическая связь четырех валентных электронов. При абсолютном нуле температуры все электроны связаны, и кристалл является изолятором. Но при комнатных температурах некоторые электроны, получив достаточную энергию теплового движения, могут оторваться от атома, стать свободными. Одновременно образуется вакантная, незаполненная связь, которую может занять какой-либо электрон из соседних атомов, оставив после себя вакантную связь, которую может занять следующий электрон. Прыжки большого числа электронов эквивалентны перемещению положительного электрического заряда, так называемой «дырки». В электрическом поле электроны и дырки перемещаются в противоположных направлениях, создавая электрический ток. С ростом температуры число свободных электронов и дырок растет, что приводит к уменьшению сопротивления.
Деление твердых тел на проводники, полупроводники и изоляторы объясняет зонная теория. В свободных атомах электроны имеют совершенно одинаковый дискретный набор дозволенных уровней энергии. Но при объединении N ≈ 1023 атомов в кристалл электроны взаимодействуют не с одним, а со всеми атомами кристалла. В результате некоторый уровень энергии свободного атома в кристалле «расщепляется» на N уровней с ничтожно малой (10 –23 эВ) разностью энергий. Эти N уровней энергии образуют энергетическую зону. Каждый уровень энергии в зоне, согласно принципу Паули, могут занимать не более двух электронов.
Для объяснения электрических, тепловых, оптических свойств достаточно рассматривать две высшие зоны: валентную зону, образованную расщеплением основного уровня энергии валентных электронов, и зону проводимости, образованную расщеплением уровня энергии возбужденных электронов.
 Кристалл является проводником, если в валентной зоне есть свободные уровни энергии или она перекрывается с зоной проводимости. Под действием электрического поля электроны и дырки имеют право перемещаться в кристалле с увеличением скорости, занимая все более высокие уровни энергии.
Кристалл является проводником, если в валентной зоне есть свободные уровни энергии или она перекрывается с зоной проводимости. Под действием электрического поля электроны и дырки имеют право перемещаться в кристалле с увеличением скорости, занимая все более высокие уровни энергии.
Кристалл является полупроводником, если валентная зона заполнена полностью, а зона проводимости отделена так называемой запрещенной зоной, ширина которой не более 2 электрон-вольт. При нуле абсолютной температуры ни тепловое движение, ни электрическое поле не в состоянии сообщить добавочную энергию электрону для перехода в зону проводимости и кристалл является изолятором. Но при комнатной температуре энергия теплового движения уже достаточна для ионизации атомов. Освободившиеся электроны переходят в зону проводимости и получают право перемещаться по кристаллу. Концентрация свободных электронов определяется распределением Больцмана:
 . (1)
. (1)
Здесь n 0 – концентрация всех валентных электронов, Ε – ширина запрещенной зоны или энергия активации, кТ – мера энергии теплового движения электрона, равная произведению постоянной Больцмана на температуру. Сопротивление кристалла обратно пропорционально концентрации электронов в зоне проводимости и дырок в валентной зоне, поэтому
 . (2)
. (2)
Здесь R 0 – сопротивление полупроводника, если бы все валентные электроны стали свободными. Коэффициент «2» учитывает энергию активации, приходящуюся на два возникающих вместе заряда – на электрон и дырку.

Влияние примесей в полупроводниках на электропроводность также объясняет зонная теория. Если, например, в кристалл 4-валентного полупроводника внести атом 5-валентной примеси, например фосфора, то один электрон окажется слабо связан с ядром атома. Его энергия будет чуть меньше, чем у свободных электронов и его энергетический уровень будет расположен близко ко дну зоны проводимости (рис. 2). Этот уровень энергии называется донорным. Энергия активации Едон для перехода электрона с донорного уровня в зону проводимости сравнительно мала. В кристалле, в зоне проводимости появляются электроны, они являются основными носителями электрического заряда. Это полупроводники n -типа.
Если в кристалл 4-валентного полупроводника внести атомы 3-валентной примеси, например индия, бора, то одна связь окажется незаполненной. Образуется дырка. Энергия электрона, занявшего дырку, немного больше, чем у других валентных электронов. Этот уровень энергии, называемый акцепторным, чуть выше потолка валентной зоны. Получив добавочную энергию Еакц,, на акцепторный уровень переходят электроны из валентной зоны, а в валентной зоне остается дырка. Дырки являются основными носителями заряда. Такие кристаллы называются полупроводниками p -типа (рис. 2).
Примесная составляющая сопротивления полупроводников определяется формулой
 . (3)
. (3)
Полная электропроводность кристалла полупроводника складывается из собственной и примесной. При сравнительно низких температурах главную роль играет примесная проводимость, так как энергия активации примеси невелика. Но с ростом температуры рост концентрации электронов, или дырок, при почти полной ионизации сравнительно небольшого числа атомов примеси прекратится. Зато растет число электронов и дырок при ионизации собственных атомов кристалла. Собственная проводимость становится преобладающей при высоких температурах.
Если уравнения (2) и (3) прологарифмировать, то получим линейные уравнения для собственной и для примесной проводимости:
 , (4)
, (4) 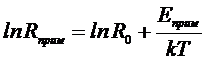 . (5)
. (5)

Логарифмы обоих видов сопротивлений линейно зависят от обратной температуры (рис. 3). Их угловые коэффициенты соответственно будут равны  . Таким образом, можно по графику определить энергию активации. Если она будет около электрон-вольта, то это собственный полупроводник, если доли электрон-вольта, то это примесный полупроводник.
. Таким образом, можно по графику определить энергию активации. Если она будет около электрон-вольта, то это собственный полупроводник, если доли электрон-вольта, то это примесный полупроводник.
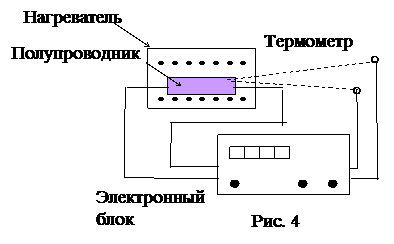
Исследование температурной зависимости сопротивления полупроводника проводится на установке (рис. 4). Полупроводником является терморезистор, помещенный в электронагреватель. Температура и сопротивление определяются по показаниям индикаторов электронного блока.
ВЫПОЛНЕНИЕ РАБОТЫ
1. Включить нагреватель и электронный блок в сеть 220 В. Переключатель на нагревателе установить в положение «3» (полупроводник). Определить начальную (комнатную) температуру и сопротивление полупроводника. Записать в таблицу.
 2. Нажать кнопку «Нагрев» на передней панели блока. Засветится лампочка нагревателя, а на индикаторе появится надпись «Warm». По мере нагрева, примерно через каждые 20 оС записывать результаты измерения сопротивления и температуры. Для удобства можно ненадолго зафиксировать результаты индикации, нажав, а затем еще раз нажав кнопку «Стоп инд.». Произвести не менее пяти измерений. Результаты записать в таблицу. Не нагревать выше 120 оС.
2. Нажать кнопку «Нагрев» на передней панели блока. Засветится лампочка нагревателя, а на индикаторе появится надпись «Warm». По мере нагрева, примерно через каждые 20 оС записывать результаты измерения сопротивления и температуры. Для удобства можно ненадолго зафиксировать результаты индикации, нажав, а затем еще раз нажав кнопку «Стоп инд.». Произвести не менее пяти измерений. Результаты записать в таблицу. Не нагревать выше 120 оС.
Выключить установку.
3. Произвести расчеты. Определить абсолютную температуру в каждом опыте: T = 273 + t и обратные значения абсолютных температур в каждом опыте с точностью до трех значащих цифр (нули перед цифрами не являются значащими). Определить натуральные логарифмы сопротивлений полупроводника.
| Сопротивление R, Ом | |||||||
| Температура t , оС | |||||||
| Абсолют. температура Т, К | |||||||
| Логарифм сопротивления ln, R | |||||||
| Обратная температура 1 /T, 1/К |
4. Построить график зависимости логарифма сопротивления от обратной температуры, ln R от 1 /T. Размер графика не менее половины страницы. В начале координат поместить округленные значения ln R и 1 /T, близкие к наименьшему значению результатов. На осях координат нанести равномерный масштаб. Провести около точек прямую линию так, чтобы отклонения точек были минимальны.
 |
5. Определить энергию активации полупроводника графическим методом. Для этого на экспериментальной прямой линии как на гипотенузе построить треугольник (рис. 3). По координатам вершин рассчитать среднее значение энергии активации
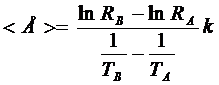 , (6)
, (6)
где k = 1,38∙10 –23 Дж/К – постоянная Больцмана. Результат перевести в электрон-вольты (1 эВ = 1,6∙10–19 Дж).
6. Оценить случайную погрешность измерения графическим методом:
 , (7)
, (7)
где n – число измерений.
7. Записать результат Е = <E> ± δE, Р = 90%. Определить тип проводимости по величине энергии активации.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите основные свойства полупроводников.
2. Объясните образование энергетических зон в кристаллах. Что называется зоной проводимости, валентной зоной и запрещенной зоной кристалла?
3. Объясните деление кристаллов на проводники, полупроводники и изоляторы в зонной теории.
4. Объясните способы получения полупроводников n- типа и р- типа. Что в них является носителями электрического заряда?
5. Объясните зависимость проводимости или сопротивления полупроводников от температуры. Почему примеси в полупроводнике влияют на электропроводность?
6. Дайте определение энергии активации. Как экспериментально определяется в лабораторной работе энергия активации полупроводника?
Работа 44
Не нашли, что искали? Воспользуйтесь поиском: