Условие дифракционных минимумов

(1.21)

где φ _m – угол дифракции; m - порядок соответствующего максимума (минимума).

Дифракционная решетка представляет собой систему большого числа N одинаковых по ширине и параллельных друг другу прозрачных щелей шириной а и непрозрачных участков шириной b. Величина

d = а + b (1.22)

называется постоянной, или периодом решетки.

Условие главных максимумов при дифракции на решетке

(1.23)

Условие дополнительных минимумов

(1.24)

где m ´ = 1, 2,…, N - 1, N + 1,…; N – полное число штрихов дифракционной решетки. Величина m ´ принимает все целочисленные значения, кроме 0, N, 2 N,…, т.е. кроме тех, при которых условие (1.24) переходит в (1.23).

Разрешающей способностью любого спектрального прибора называется величина

(1.24)

Здесь Δ λ = λ₁- λ₂ – разрешимый интервал длин волн; λ = (λ₁ + λ₂)/ 2 – середина интервала Δ λ.

Для дифракционной решетки c числом штрихов N в m -ом порядке спектра разрешающая способность равна

R = mN. (1.25)

При дифракции рентгеновского излучения на пространственной кристаллической решетке условие максимумов имеет вид

(1.26)

где d - расстояние между атомными плоскостями кристалла; θ _m – угол между направлением падающего излучения и гранью кристалла, называемый углом скольжения. Последнее выражение называется формулой Вульфа - Брэгга.

ПРИМЕР. На щель шириной а = 0,1 мм нормально падает параллельный пучок монохроматического света длины волны λ = 500 нм. Дифракционная картина наблюдается на экране, расположенном на расстоянии L от щели. Ширина изображения щели b на экране составляет 1 см. Найти величину L.

РЕШЕНИЕ. Шириной изображения щели считается расстояние между первыми минимумами (рис.7). Угол φ₁ показывает направление на первый дифракционный минимум, условие которого согласно (1.21) можно записать

(1.27)

Величину L можно определить из прямоугольного треугольника АВС из соотношения

tg φ₁ = b /2L,

заменяя tg φ₁ на sin φ₁, что возможно при малых углах:

L = b /2 sin φ₁

Используя соотношение (1.27), окончательно получим

L = bа /2 λ.

Подставим в численный расчет все величины в системе СИ:

0,1∙10^-3∙1∙10^-2

L = ––––––––-––– = 1 (м).

2∙5∙10^-7

ПРИМЕР. Постоянная дифракционной решетки 10 мкм, ее ширина 2 см. В спектре какого порядка эта решетка может разрешить дублет λ₁ = 486,0 нм и λ₂ = 486,1 нм?

РЕШЕНИЕ. Разрешающая способность дифракционной решетки

λ

R = ––- = mN,

Δ λ

где Δ λ — минимальная разность длин волн двух спектральных линий λ и λ + Δ λ, разрешаемых решеткой; т — порядок спектра; N — число щелей решетки.

Поскольку постоянная решетки d есть расстояние между сере­динами соседних щелей, общее число щелей можно найти как

N = l / d,

где l — ширина решетки.

Из этих двух формул находим:

λ d λ

Δλ = ––––– = ––––.

mN ml

Дублет спектральных линий λ₁ и λ₂ будет разрешен, если

Δ λ ≤ λ₂ - λ₁.

Учитывая, что λ = (λ₁ + λ₂ )/2 получим

d (λ₁ + λ₂ )

––––––––- ≤ λ₂ - λ₁,

2 ml

откуда следует, что дублет λ₁ и λ₂ будет разрешен во всех спектрах с порядком

d (λ₁ + λ₂ )

m ≥ ––––––––––-.

2 l (λ₂ - λ₁ )

Подставляя числовые данные, получим

10 ·10 ^-6 м · (486,0· + 486,1)10 ^-9 м

m ≥ ––––––––––––––––––––––––––––––––– = 2,43.

2·10 ^-6 м (486,1-486,0) 10 ^-9 м

Так как т — целое число, то т ≥ 3.

ПОЛЯРИЗАЦИЯ СВЕТА

Поляризованным называется свет, в котором колебания вектора напряженности электрического поля Е (светового вектора), упорядочены каким либо образом. Если световой вектор электромагнитной волны колеблется в определенной плоскости, его можно назвать плоскополяризованным., или неполяризованный свет имеет всевозможные направления колебания вектора Е. Световой вектор при этом всегда перпендикулярен направлению распространения световой волны, поэтому можно сказать, что электромагнитные волны поперечно поляризованы. На рис.8 показано, как изображаются волны различной поляризации.

Устройства, позволяющие получить плоскополяризованный свет, называются поляризаторами.

Закон Малюса для плоскополяризованного света имеет вид

I = I ₀ cos² α, (1.27)

где I ₀ и I — интенсивность плоско­поляризованного света, па­дающего и прошед­шего че­рез идеальный поляризатор; α — угол между плос­костью по­ляризации падающего све­та и главной плоскостью поляризатора.

Если через поляризатор пропускать естественный свет, то угол α будет быстро и беспорядочно принимать с равной вероятностью все значения от 0 до 90˚, и интенсивность света, прошедшего через поляризатор

I = I ₀ <cos² α> = 0,5 I _0, (1.28)

где <cos² α> = 0,5 – среднее значение cos² α за достаточно большой промежуток времени.

Закон Брюстера (1.29)

где i _Б — угол Брюстера, при котором отраженный от поверхности диэлектрика свет полностью поляризован; n ₁ и n ₂ — показатели преломле­ний первой и второй сред.

Вещества, вращающие плоскость поляризации световой волны, называются оптически активными.

Угол поворота плоскости поляризации оптически активными кристаллами и чистыми жидкостями

φ = α d, (1.30)

оптически активными растворами

φ = [α] d C, (1.31)

где d – толщина слоя оптически активного вещества; С - его массовая концентрация.

Некоторые прозрачные кристаллы, являясь анизотропными веществами, обладают свойством двойного лучепреломления, т. е. при попадании на него луч света раздваивается на два луча – обыкновенный (о) и необыкновенный (е) с разными свойствами. У них разные законы преломления и показатели преломления n _о и n _е , взаимно перпендикулярная поляризация.

Двойное лучепреломление может возникать и в изотропных телах, которые становятся анизотропными под воздействием электрического поля напряженности Е (эффект Керра). Разность показателей преломления обыкновенного и необыкновенного лучей в этом случае

n _о - n _е = k Е ², (1.32)

где k - постоянная Керра данного материала.

ПРИМЕР. Естественный свет проходит через систему из трех одинаковых поляроидов, в каждом которых из-за отражения и поглощения света теряется 20% падающего на него излучения. Плоскости поляризации первого и второго поляроидов составляют угол α ₁ = 30˚, а первого и третьего – 90˚ (рис.9). Во сколько раз уменьшится интенсивность света, вышедшего из этой системы?

РЕШЕНИЕ. Обозначим интенсивности естественного света, падающего на первый поляризатор П₁ через а I ₀, вышедшего из первого, второго и третьего поляроидов – I ₁, I ₂ и I ₃ соответственно. Пластинками П₁, П₁, П ₃ изобразим поляроиды, пунктирными прямыми ОО₁, ОО₂ , ОО₃ укажем положение их плоскостей поляризации. После прохождения каждого из поляризаторов колебания светового вектора Е будет происходить параллельно ОО₁, ОО₂ , ОО₃. Рассмотрим прохождение света последовательно через каждый поляроид. Если бы поляроиды были идеальными, то интенсивности света, проходящего через них, можно было определить по формулам (1.28) и (1.27). С учетом 20% потерь запишем:

I ₁ = 0,5 I ₀ (1- 0,2);

I ₂ = I ₁ cos² α₁(1- 0,2) = 0,5 I ₀ (1- 0,2)²;

I ₃ = I ₂ cos² (α₂ -α₁) (1- 0,2) = 0,5 I ₀ (1- 0,2)³.

Тогда

т.е. интенсивность вышедшего света уменьшится в 20,8 раз.

ПРИМЕР. Определить показатель преломления прозрачного вещества, если угол Брюстера при падении на него света из воздуха оказался равным предельному углу.

РЕШЕНИЕ. Обозначим искомый показатель преломления n _х, показатель преломления воздуха n ₁. Закон Брюстера (1.29) запишем в виде

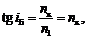(1.33)

т.к. для воздуха n ₁ = 1.

Полное внутреннее отражение имеет место при переходе светового луча из неизвестной прозрачной среды в воздух. Используем закон преломления света (1.3) с учетом, что β = 90˚ и sin 90˚= 1

(1.34)

Преобразуем формулу (1.33) следующим образом:

(1.35)

Учитывая, что по условию задачи i _бр = α_пр, имеем

(1.36)

Подставив вместо sin α_пр величину 1/ n _х, согласно уравнению (1.34), получим

(1.37)

Произведем замену переменных n _x² = t. Тогда последнее уравнение (1.37) примет вид

t ² - t - 1= 0.

Оно имеет два решения:

Исходя из физического смысла, выберем решение

Тогда

Не нашли, что искали? Воспользуйтесь поиском: