Дифракция от одной щели. Пусть на длинную щель шириной a падает плоская волна (рис.22)

Пусть на длинную щель шириной a падает плоская волна (рис.22). Плоскость фронта волны параллельна плоскости щели. Когда фронт дойдет до щели и займет положение АВ, то все его точки станут новыми источниками волн, распространяющими свет во все стороны от щели. Рассмотрим лучи, идущие под углом j к первоначальному направлению. После прохождения через линзу L эти лучи соберутся в одной точке в фокальной плоскости линзы. Поставив в эту плоскость экран E, можно на нем наблюдать результат интерференции волн, распространяющихся под разными углами.

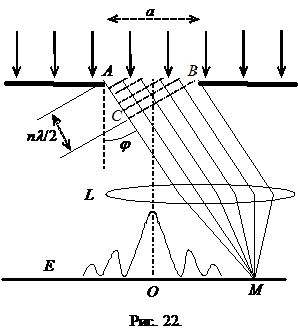
Для расчета результата интерференции разобьем фонт волны на зоны Френеля. Опустим из точки B перпендикуляр BС на луч, идущий от точки A. Разделим AС на отрезки длиной l /2. На AС уложится n = 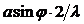таких отрезков. Проведя из концов этих отрезков линии, параллельные BС, до встречи с АВ, мы разобьем щель на n полосок одинаковой ширины. Эти полоски и являются зонами Френеля. Волны от полосок, находящихся рядом, идут в точку наблюдения с разностью хода l /2 и поэтому гасят друг друга. Если в некотором направлении число зон окажется четным, то на экране будет минимум освещенности. Условие минимума определится из условия

a ×sin j _мин = 2 k × l /2 = kl.

В промежутках между минимумами будут максимумы, направление на которые определится из условия

a ×sin j _мах = (2 k + 1) l /2.

Центральный, наиболее яркий максимум будет расположен против центра щели. По обе его стороны интенсивность света вначале будет спадать до первого минимума, а затем возрастать до следующего максимума и т.д.

Если щель узкая (а < l /2), то вся поверхность щели будет одной зоной при всех углах. Условие минимума станет выполнить невозможно, и свет достигнет всех точек экрана.

Не нашли, что искали? Воспользуйтесь поиском: