Интерференция света в тонких пленках. Интерференционные полосы равного наклона

Интерференционные полосы равного наклона. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала.

Рассмотрим сначала плоскопараллельную пластинку толщины с показателем преломления (рис. 2.11). Пусть на пластинку падает плоская световая волна, которую можно рассматривать как параллельный пучок лучей. Пластинка отбрасывает вверх два параллельных пучка света, один из которых образовался за счет отражения от верхней поверхности пластинки, второй – вследствие отражения от нижней поверхности. Каждый из этих пучков представлен на рис. 2.11 только одним лучом.

При входе в пластинку и при выходе из нее пучок 2 претерпевает преломление. Кроме двух пучков 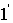и , пластинка отбрасывает вверх пучки, возникающие в результате трех-, пяти- и т.д. кратного отражения от поверхностей пластинки. Однако ввиду малой интенсивности их можно не принимать во внимание.

Рассмотрим интерференцию лучей, отраженных от пластинки. Поскольку на пластинку падает плоская волна, то фронт этой волны представляет собой плоскость, перпендикулярную лучам 1 и 2. На рис. 2.11 прямая ВС представляет собой сечение волнового фронта плоскостью рисунка. Оптическая разность хода, приобретаемая лучами 1 и 2 до того, как они сойдутся в точке С, будет

,

(2.13)

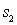где – длина отрезка ВС, а – суммарная длина отрезков АО и ОС. Показатель преломления среды, окружающей пластинку, полагаем равным единице. Из рис. 2.11 видно, что , . Подстановка этих выражений в (2.13) дает . Воспользуемся законом преломления света: 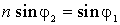; и учтем, что 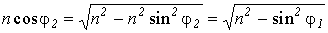, тогда для разности хода получим следующее выражение: .

При вычислении разности фаз между колебаниями в лучах и 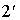нужно, кроме оптической разности хода D, учесть возможность изменения фазы при отражении в точке С. В точке С отражение волны происходит от границы раздела среды оптически менее плотной со средой оптически более плотной. Поэтому фаза волны претерпевает изменение на p. В точке отражение происходит от границы раздела среды оптически более плотной со средой оптически менее плотной, и скачка фазы в этом случае не происходит. Качественно это можно представить себе следующим образом. Если толщину пластинки устремить к нулю, то полученная нами формула для оптической разности хода дает . Поэтому при наложении лучей и 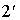должно происходить усиление колебаний. Но это невозможно, так как бесконечно тонкая пластинка вообще не может оказывать влияния на распространение света. Поэтому волны, отраженные от передней и задней поверхности пластинки, должны при интерференции гасить друг друга. Их фазы должны быть противоположны, то есть оптическая разность хода D при d→0 должна стремиться к . Поэтому к прежнему выражению для D нужно прибавить или вычесть , где λ₀ – длина волны в вакууме. В результате получается:

.

(2.14)

Итак, при падении на пластинку плоской волны образуются две отраженные волны, разность хода которых определяется формулой (2.14). Эти волны могут интерферировать, если оптическая разность хода не превышает длину когерентности. Последнее требование для солнечного излучения приводит к тому, что интерференция при освещении пластинки наблюдается только в том случае, если толщина пластинки не превышает нескольких сотых миллиметра.

Практически интерференцию от плоскопараллельной пластинки наблюдают, поставив на пути отраженных пучков линзу, которая собирает пучки в одной из точек экрана, расположенного в фокальной плоскости линзы. Освещенность в этой точке зависит от оптической разности хода. При получаются максимумы, при – минимумы интенсивности. Следовательно, условие максимумов интенсивности имеет вид:

,

(2.15)

а минимумов:

.

(2.16)

Эти соотношения получены для отраженного света.

Пусть тонкая плоскопараллельная пластинка освещается рассеянным монохроматическим светом. Расположим параллельно пластинке линзу, в фокальной плоскости которой поместим экран (рис. 2.12). В рассеянном свете имеются лучи самых разнообразных направлений. Лучи, параллельные плоскости рисунка и падающие на пластинку под углом 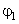, после отражения от обеих поверхностей пластинки соберутся линзой в точке и создадут в этой точке освещенность, определяемую значением оптической разности хода. Лучи, идущие в других плоскостях, но падающие на пластику под тем же углом, соберутся линзой в других точках, отстоящих от центра экрана 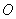на такое же расстояние, как и точка . Освещенность во всех этих точках будет одинакова. Таким образом, лучи, падающие на пластинку под одинаковым углом 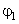, создадут на экране совокупность одинаково освещенных точек, расположенных по окружности с центром точке О. Аналогично, лучи, падающие под другим углом , создадут на экране совокупность одинаково освещенных точек, расположенных по окружности другого радиуса 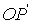. Но освещенность этих точек будет иной, так как им соответствует другая оптическая разность хода.

В результате на экране возникнет совокупность чередующихся темных и светлых круговых полос с общим центром в точке О. Каждая полоса образована лучами, падающими на пластину под одинаковым углом. Поэтому получающиеся в этом случае интерференционные полосы называютсяполосами равного наклона.

Согласно (2.15) положение максимумов интенсивности зависит от длины волны , поэтому в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных цветов, и интерференционная картина приобретет радужную окраску.

Для наблюдения полос равного наклона экран должен располагаться в фокальной плоскости линзы, так, как его располагают для получения бесконечно удаленных предметов. Поэтому говорят, что полосы равного наклона локализованы в бесконечности. Роль линзы может играть хрусталик глаза, а экрана – сетчатка глаза.

Интерференционные полосы равной толщины.Возьмем теперь пластинку в виде клина. Пусть на нее падает параллельный пучок лучей (рис. 2.13). Но теперь лучи, отразившись от разных поверхностей пластинки, не будут параллельными. Два до падения на пластинку практически сливающихся луча 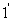после отражения от верхней и нижней поверхностей клина пересекаются в точке . Два практически сливающихся луча после отражения пересекаются в точке . Можно показать, что точки и лежат в одной плоскости, проходящей через вершину клина О.

Если расположить экран Э так, чтобы он проходил через точки и , на экране возникнет интерференционная картина. При малом угле клина разность хода лучей, отраженных от его верхней и нижней поверхностей, можно с достаточной степенью точности вычислить по формуле , полученной для плоскопараллельной пластинки, беря в качестве толщину клина в месте падения на нее лучей. Поскольку разность хода лучей, отразившихся от разных участков клина, теперь неодинакова, освещенность будет неравномерной – на экране появятся светлые и темные полосы. Каждая из таких полос возникает в результате отражения от участков клина с одинаковой толщиной, вследствие чего их называют полосами равной толщины.

Таким образом, интерференционная картина, получающаяся при отражении от клина плоской волны, оказывается локализованной в некоторой области вблизи поверхности клина. По мере удаления от вершины клина растет оптическая разность хода, и интерференционная картина становится все менее отчетливой.

Рис. 2.14

При наблюдении в белом свете полосы будут окрашенными, так что поверхность пластинки будет иметь радужную окраску. В реальных условиях при наблюдении, например, радужных цветов на мыльной пленке изменяется как угол падения лучей, так и толщина пленки. В этом случае наблюдаются полосы смешанного типа.

Полосы равной толщины легко наблюдать на плоской проволочной рамке, которую окунули в мыльный раствор. Затягивающая её мыльная плёнка покрывается горизонтальными интерференционными полосами, получившимися при интерференции волн, отразившихся от разных поверхностей пленки (рис. 2.14). С течением времени мыльный раствор стекает, и интерференционные полосы съезжают вниз.

Если проследить за поведением сферического мыльного пузыря, то легко обнаружить, что его поверхность покрыта цветными кольцами, медленно сползающими к его основанию. Смещение колец говорит о постепенном утончении стенок пузыря.

Кольца Ньютона

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плоско-выпуклой линзы с большим радиусом кривизны (рис. 2.15). Роль тонкой пленки, от поверхности которой отражаются волны, играет воздушный зазор между пластинкой и линзой (вследствие большой толщины пластинки и линзы за счет отражений от других поверхностей интерференционные полосы не возникают). При нормальном падении света полосы равной толщины имеют вид окружностей, при наклонном – эллипсов.

Найдем радиусы колец Ньютона, получающихся при падении света по нормали к пластинке. В этом случае и 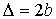. Из рис. 2.15 видно, что , где – радиус кривизны линзы, 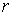– радиус окружности, всем точкам которой соответствует одинаковый зазор . Величиной можно пренебречь, тогда 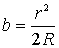. Чтобы учесть возникающее при отражении от пластинки изменение фазы на p, нужно добавить к разности хода :

.

(2.17)

В точках, для которых , возникнут максимумы интенсивности, а в точках, для которых – минимумы интенсивности. Оба условия можно объединить в одно:

,

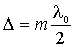(2.18)

четным 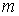будут соответствовать максимумы, а нечетным – минимумы интенсивности. Подставив (2.18) в (2.17), получим радиусы темных и светлых колец Ньютона:

.

(2.19)

Четным 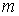соответствуют радиусы светлых колец, нечетным 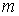– радиусы темных колец. Значению соответствует , то есть в месте касания пластинки и линзы наблюдается минимум интенсивности, обусловленный изменением фазы на p при отражении световой волны от пластинки.

Рис. 2.16

На рис. 2.16 представлен вид интерференционных колец Ньютона в красном и зеленом свете. Так как длина волны красного света больше, чем зеленого, то радиусы колец в красном свете больше радиусов колец с таким же номером в зеленом свете.

Если в установке Ньютона линзу перемещать вверх параллельно самой себе, то из-за увеличения толщины воздушной прослойки каждая окружность, соответствующая постоянной разности хода, будет стягиваться к центру картины. Достигнув центра, интерференционное кольцо превращается в кружок, исчезающий при дальнейшем перемещении линзы. Таким образом, центр картины будет попеременно становиться то светлым, то темным. Одновременно на периферии поля зрения будут зарождаться и перемещаться к центру новые интерференционные кольца, пока каждое из них не исчезнет в центре картины. При перемещении линзы непрерывно вверх пропадают кольца самых низких порядков интерференции и зарождаются кольца более высоких порядков.

Пример
Просветление оптики

Просветление оптики делается для уменьшения коэффициентов отражения поверхностей оптических деталей путём нанесения на них одной или нескольких непоглощающих плёнок. Без просветляющих плёнок потери на отражение света могут быть очень большими. В системах с большим числом поверхностей, например, в сложных объективах, потери света могут достигать 70 % и более, что ухудшает качество изображений, формируемых такими оптическими системами. Устранить это можно с помощью просветления оптики, которое является одним из важнейших применений интерференции в тонких пленках.

При отражении света от передней и задней поверхности пленки, нанесенной на оптическую деталь, в отраженном свете образуется минимум интенсивности в результате интерференции, а следовательно, в проходящем свете будет максимум интенсивности для этой длины волны. При нормальном падении света эффект будет максимален, если толщина тонкой плёнки равна нечётному числу четвертей длины световой волны в материале плёнки. Действительно, в этом случае потери половины длины волны при отражении не происходит, так как и на верхней, и на нижней поверхностях пленки волна отражается от границы раздела среды оптически менее плотной и оптически более плотной. Поэтому условие максимума интенсивности примет вид . Отсюда получим .

Изменяя толщину просветляющей плёнки, можно сместить минимум отражения в различные участки спектра.

Не нашли, что искали? Воспользуйтесь поиском: