
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Двухлучевые интерферометры. Явление интерференции лежит в основе устройств, которые называются интерферометрами
Явление интерференции лежит в основе устройств, которые называются интерферометрами. Принцип действия всех интерферометров одинаков, и различаются они лишь методами получения когерентных волн. Пучок света с помощью того или иного устройства пространственно разделяется на два или большее число когерентных пучков, которые проходят различные оптические пути, а затем сводятся вместе. В точке схождения пучков наблюдаются интерференционные максимумы или минимумы. Форма и взаимное расположение интерференционных максимумов и минимумов зависит от способа разделения пучка света на когерентные пучки, от числа интерферирующих пучков, их оптической разности хода, спектрального состава света.
Интерферометры позволяют с высокой точностью измерять линейные и угловые размеры, показатели преломления веществ, исследовать структуру спектральных линий и т.д. В зависимости от назначения они отличаются конфигурацией.
Интерферометр Майкельсона. Рассмотрим подробно схему и принцип действия интерферометра Майкельсона – ученого, сыгравшего большую роль в истории науки.
 В интерферометре Майкельсона (рис. 2.17) свет от источника
В интерферометре Майкельсона (рис. 2.17) свет от источника  падает на полупрозрачную пластинку
падает на полупрозрачную пластинку  , расположенную под углом 45° к направлению распространения луча. На пластинке
, расположенную под углом 45° к направлению распространения луча. На пластинке  он разделяется на две волны, распространяющиеся к зеркалам
он разделяется на две волны, распространяющиеся к зеркалам  и
и  . После отражения от зеркал
. После отражения от зеркал  и
и  волны распространяются в направлении трубы Т и могут интерферировать. Пластинка
волны распространяются в направлении трубы Т и могут интерферировать. Пластинка  , тождественная с пластинкой
, тождественная с пластинкой  , компенсирует разность хода, возникающую из-за того, что один пучок пересекает пластинку
, компенсирует разность хода, возникающую из-за того, что один пучок пересекает пластинку  три раза, а другой – только один раз. В результате разность хода лучей, распространяющихся строго вдоль оси интерферометра, определяется разностью длин плеч
три раза, а другой – только один раз. В результате разность хода лучей, распространяющихся строго вдоль оси интерферометра, определяется разностью длин плеч  и
и  (расстояний от
(расстояний от  до
до  и
и  ):
):
 .
.
Возникающая при этом разность фаз  . Здесь не учитывается изменение фаз при отражении от зеркал и пластин. Это можно сделать, но ничего нового в этом случае не наблюдается, так как вносимая при этом дополнительная разность хода кратна
. Здесь не учитывается изменение фаз при отражении от зеркал и пластин. Это можно сделать, но ничего нового в этом случае не наблюдается, так как вносимая при этом дополнительная разность хода кратна  .
.
Распределение интенсивности зависит от разности фаз  . Суммарная интенсивность максимальна, когда
. Суммарная интенсивность максимальна, когда  , то есть
, то есть  ,
,  , и равна нулю при
, и равна нулю при  и
и  .
.
Главная особенность интерферометра Майкельсона заключается в том, что, передвигая одно из зеркал с помощью винтов  , можно непрерывно изменять разность хода, наблюдая при этом интерференционную картину. Если зеркала расположить под углом друг к другу (рис. 2.17б), то можно наблюдать полосы равной толщины.
, можно непрерывно изменять разность хода, наблюдая при этом интерференционную картину. Если зеркала расположить под углом друг к другу (рис. 2.17б), то можно наблюдать полосы равной толщины.
Интерферометр Жамена. В интерферометре Жамена деление лучей происходит в толстых, не менее 20 мм, пластинах, изготовленных из однородного стекла или кварца (рис. 2.18).  Пластины располагаются под углом 45° к направлению падающего луча. В результате отражения от передней и задней граней пластин
Пластины располагаются под углом 45° к направлению падающего луча. В результате отражения от передней и задней граней пластин  и
и  образуются четыре луча. Лучи 2 и 3 пространственно совмещены и могут интерферировать. Каждая пластина вносит разность хода
образуются четыре луча. Лучи 2 и 3 пространственно совмещены и могут интерферировать. Каждая пластина вносит разность хода  . Поэтому разность хода лучей 2 и 3 равна
. Поэтому разность хода лучей 2 и 3 равна  , где
, где  и
и  – углы преломления в пластинах
– углы преломления в пластинах  и
и  . Разность хода тем больше, чем толще пластины. Если пластины установлены параллельно друг другу, то
. Разность хода тем больше, чем толще пластины. Если пластины установлены параллельно друг другу, то  – поле будет равномерно освещено. При юстировке одну из пластин немного наклоняют, поворачивая вокруг горизонтальной оси. Тогда углы
– поле будет равномерно освещено. При юстировке одну из пластин немного наклоняют, поворачивая вокруг горизонтальной оси. Тогда углы  и
и  будут немного отличаться, и интерференционная картина представляет горизонтальные полосы равной толщины малых порядков, которые можно наблюдать в зрительную трубу, установленную на бесконечность. Пучки между пластинами пространственно разделены, что позволяет поместить на их пути кюветы длиной
будут немного отличаться, и интерференционная картина представляет горизонтальные полосы равной толщины малых порядков, которые можно наблюдать в зрительную трубу, установленную на бесконечность. Пучки между пластинами пространственно разделены, что позволяет поместить на их пути кюветы длиной  с исследуемыми веществами. При этом оптическая разность хода лучей изменится на величину
с исследуемыми веществами. При этом оптическая разность хода лучей изменится на величину  , что вызовет смещение интерференционной картины на m полос. Из условия
, что вызовет смещение интерференционной картины на m полос. Из условия 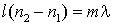 можно определить
можно определить  с точностью до
с точностью до  и более.
и более.
Интерферометр Жамена труден в изготовлении, так как сложно получить однородные толстые пластины. Кроме того, толстые пластины медленно прогреваются, и интерференционная картина ползет часами. Трудно проводить исследования в ультрафиолетовой области, для нее требуются кварцевые пластины (обычное стекло поглощает ультрафиолетовое излучение), а они хрупкие.
От всех этих недостатков свободен интерферометр Рождественского.
 Интерферометр Рождественского. В интерферометре Рождественского роль делителей пучков играют полупрозрачные пластины
Интерферометр Рождественского. В интерферометре Рождественского роль делителей пучков играют полупрозрачные пластины 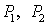 и зеркала
и зеркала  (рис. 2.19). Здесь пучки значительно пространственно разведены без использования толстых пластин, и можно легко ввести кюветы с исследуемым веществом. Таким образом, можно изучать физические процессы, которые ведут к изменению показателя преломления, например, при нагревании.
(рис. 2.19). Здесь пучки значительно пространственно разведены без использования толстых пластин, и можно легко ввести кюветы с исследуемым веществом. Таким образом, можно изучать физические процессы, которые ведут к изменению показателя преломления, например, при нагревании.
ДИФРАКЦИЯ СВЕТА
Явление дифракции
Дифракцией называется совокупность явлений, наблюдаемых при распространении волн в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция – характерная особенность распространения волн независимо от их природы. Именно дифракция звуковых волн объясняет возможность слышать голос человека, находящегося за углом дома.
 Рис. 3.1
Рис. 3.1
|
Мы ежедневно сталкиваемся с дифракцией радиоволн, слушая радиопередачи и пользуясь сотовым телефоном. Дифракция приводит к огибанию электромагнитными волнами препятствий и проникновению их в область геометрической тени. Из-за дифракции тень от препятствия с прямым краем не бывает идеально резкой: при освещении непрозрачных экранов источником света на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдаются чередующиеся светлые и темные дифракционные полосы (рис. 3.1). Если на пути параллельного светового пучка расположено круглое препятствие, например, диск, шарик, круглое отверстие в непрозрачном экране, то на экране, расположенном на большом расстоянии от препятствия, появляется дифракционная картина в виде чередующихся светлых и темных колец.
Дифракция волн существенно зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию.
 Рис. 3.2
Рис. 3.2
|
Наиболее отчетливо дифракция обнаруживается в тех случаях, когда размер огибаемых препятствий соизмерим с длиной волны. Поэтому легко наблюдается дифракция звуковых, сейсмических и радиоволн, для которых длина волны лежит в пределах от нескольких метров до нескольких километров. Значительно труднее наблюдать дифракцию электромагнитных волн оптического диапазона, длины которых лежат в пределах  .
.
 Рис. 3.3
Рис. 3.3
|
Явление дифракции нагляднее всего демонстрируется с помощью волн на поверхности воды. Если размер отверстия или препятствия заметно меньше длины волны, то волна с ним не взаимодействует. Этим обусловлено то, что в шторм волны не проникают в бухту с узким входом. Морские волны длиннее, чем вход в бухту, и не замечают этого входа. Толщина стволов деревьев, стоящих в воде, меньше длины волны, и волны не взаимодействуют с ними (рис. 3.2).
А если размеры препятствия много больше длины волны, то волны за него не проникают, создается область тени: световая тень (рис. 3.3), звуковая тень, ограничения при передаче телевизионного сигнала, невозмущенная поверхность воды за большим валуном (рис. 3.4).
Из-за малости длины волны дифракционные явления в оптике наблюдать сложнее, чем в механике, но их проявления более многообразны и красочны.
 Рис. 3.4
Рис. 3.4
|
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, называют дифракцией волн.
В строгой постановке дифракционные задачи, ввиду их сложности, допускают аналитические решения лишь в простейших идеализированных случаях. В оптике значительно большее значение имеют приближенные методы решения дифракционных задач, основанные на принципе Гюйгенса в обобщенной формулировке Френеля.
3.2. Принцип Гюйгенса–Френеля
В XVIII столетии Христиан Гюйгенс на основе опытов с волнами на поверхности воды предложил метод построения волнового фронта. Если плоская волна падает на экран с отверстием, размер которого много меньше длины волны, то за экраном распространяется сферическая волна.
 Рис. 3.5
Рис. 3.5
|
На этом основании Гюйгенс предложил каждый элемент волнового фронта рассматривать как источник элементарных сферических волн – вторичных волн. Поскольку волновой фронт представляет совокупность точек среды, до которой дошла волна в момент времени t, то принцип Гюйгенса утверждает, что каждая точка среды, до которой доходит волновое движение, может рассматриваться как источник вторичных волн. Вторичные волны являются сферическими (рис. 3.5).
 Гюйгенс Христиан (Huygens Christiaan) (1629–1695)
Гюйгенс Христиан (Huygens Christiaan) (1629–1695)
Голландский астроном и физик. Родился в Гааге в семье дипломата. Получил хорошее домашнее образование, затем окончил Лейденский университет. В 1666 г. переехал в Париж, где принимал участие в организации Академии наук Франции.
Самую большую известность Гюйгенсу принесли работы по оптике и астрономии. Он значительно усовершенствовал конструкцию телескопов и открыл кольца Сатурна. Кроме того, Гюйгенс является изобретателем маятниковых часов.
Во всех применениях вторичные волны Гюйгенса выступают не как реальные волны, а как вспомогательные сферы, используемые для такого построения. Эти сферы, построенные из точек волнового фронта как из центров, проявляют свое действие только на огибающей, которая дает новое положение волнового фронта. При этом остается необъясненным, почему при распространении волны не возникает обратная волна. Принцип Гюйгенса не дает никаких указаний об интенсивности волн, распространяющихся в различных направлениях. Этот недостаток был устранен Френелем.
Френель предположил, что вторичные волны когерентны и поэтому при наложении интерферируют друг с другом. Свет должен наблюдаться во всех местах пространства, где при интерференции вторичные волны усиливаются; где они взаимно гасят друг друга, должна наблюдаться темнота. К огибающей все вторичные волны приходят в одинаковых фазах, и их интерференция приводит к большой интенсивности света. Качественно становится понятным и отсутствие обратной волны. Вторичные волны, идущие назад, вступают в пространство, где уже есть волновое возмущение – прямая волна. При интерференции вторичные волны гасят прямую волну, так что после прохождения волны пространство за ней оказывается невозмущенным.
Расчет волнового поля в любой точке наблюдения Р на основе принципа Гюйгенса–Френеля делается следующим образом. Выделим поверхность S, все точки которой колеблются в одной фазе. Поверхность ограничивает объем с источниками света  и т.д. (рис. 3.6). Все точки такой поверхности можно рассматривать как когерентные источники вторичных волн, распространяющихся во всех направлениях. Для того чтобы определить колебания в некоторой точке P, вызванные волной, нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S. Световое поле, возникающее в результате их интерференции, в пространстве вне поверхности S совпадает с полем реальных источников света.
и т.д. (рис. 3.6). Все точки такой поверхности можно рассматривать как когерентные источники вторичных волн, распространяющихся во всех направлениях. Для того чтобы определить колебания в некоторой точке P, вызванные волной, нужно сначала определить колебания, вызываемые в этой точке отдельными вторичными волнами, приходящими в нее от всех элементов поверхности S. Световое поле, возникающее в результате их интерференции, в пространстве вне поверхности S совпадает с полем реальных источников света.
 Амплитуда вторичной волны пропорциональна площади элемента поверхности
Амплитуда вторичной волны пропорциональна площади элемента поверхности 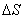 и зависит от угла j между нормалью
и зависит от угла j между нормалью  к площадке
к площадке 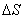 и направлением от площадки к точке наблюдения Р. Так как вторичные волны являются сферическими, то их амплитуда убывает с расстоянием по закону
и направлением от площадки к точке наблюдения Р. Так как вторичные волны являются сферическими, то их амплитуда убывает с расстоянием по закону  , где
, где  – расстояние от площадки
– расстояние от площадки 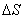 до точки Р. От каждого участка
до точки Р. От каждого участка 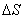 в точку наблюдения Р, лежащую перед поверхностью S, приходит колебание:
в точку наблюдения Р, лежащую перед поверхностью S, приходит колебание:
 . .
| (3.1) |
Здесь  – фаза колебаний на поверхности
– фаза колебаний на поверхности  ,
,  – волновое число,
– волновое число, 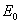 – амплитуда светового колебания в том месте, где находится площадка
– амплитуда светового колебания в том месте, где находится площадка 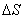 . Коэффициент
. Коэффициент  зависит от угла
зависит от угла 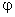 . При
. При  этот коэффициент максимален, при
этот коэффициент максимален, при  – обращается в нуль.
– обращается в нуль.
Результирующее колебание в точке Р представляет собой суперпозицию колебаний (3.1), приходящих от всей волновой поверхности S:
 . .
| (3.2) |
Эта формула является аналитическим выражением принципа Гюйгенса–Френеля. Для качественного рассмотрения простейших случаев дифракции света с помощью принципа Гюйгенса–Френеля может быть применено построение зон Френеля.
Зоны Френеля
Вычисления по формуле (3.2) представляют в общем случае трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.
 Чтобы понять суть метода, разработанного Френелем, определим амплитуду светового колебания, возбуждаемого в точке
Чтобы понять суть метода, разработанного Френелем, определим амплитуду светового колебания, возбуждаемого в точке  сферической волной, распространяющейся в изотропной однородной среде от источника
сферической волной, распространяющейся в изотропной однородной среде от источника  (рис. 3.7). Фронт такой волны симметричен относительно прямой
(рис. 3.7). Фронт такой волны симметричен относительно прямой  . Разобьем поверхность фронта на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки
. Разобьем поверхность фронта на кольцевые зоны, построенные так, что расстояния от краев каждой зоны до точки  отличаются на
отличаются на  (где
(где  – длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны называются зонами Френеля.
– длина волны в той среде, в которой распространяется волна). Обладающие таким свойством зоны называются зонами Френеля.
Если расстояние от вершины поверхности О до точки Р равно b, то расстояние от внешнего края 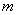 -й зоны до точки Р равно
-й зоны до точки Р равно  . Колебания, приходящие в точку Р от аналогичных точек двух соседних зон (то есть от точек, лежащих в середине зон или у внешних краев зон и тому подобное), находятся в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на
. Колебания, приходящие в точку Р от аналогичных точек двух соседних зон (то есть от точек, лежащих в середине зон или у внешних краев зон и тому подобное), находятся в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на  .
.
Покажем, что площади всех зон Френеля примерно одинаковы. Внешняя граница 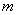 -й зоны выделяет на волновой поверхности сферический сегмент высоты
-й зоны выделяет на волновой поверхности сферический сегмент высоты  . Обозначим площадь этого сегмента
. Обозначим площадь этого сегмента  . Тогда площадь
. Тогда площадь 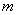 -й зоны можно представить в виде
-й зоны можно представить в виде 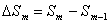 , где
, где  – площадь сферического сегмента, выделяемого внешней границей
– площадь сферического сегмента, выделяемого внешней границей  -й зоны. Из рис. 3.7 видно, что
-й зоны. Из рис. 3.7 видно, что  , где
, где  – радиус волнового фронта,
– радиус волнового фронта,  – радиус внешней границы m -й зоны. Тогда
– радиус внешней границы m -й зоны. Тогда
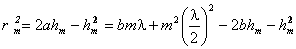 , ,
| (3.3) |
 . .
| (3.4) |
Для не слишком больших значений 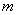 и ввиду малости l можно пренебречь в (3.4) слагаемым, содержащим
и ввиду малости l можно пренебречь в (3.4) слагаемым, содержащим  . В этом приближении
. В этом приближении
 . .
| (3.5) |
Площадь сегмента равна произведению длины окружности, ограничивающей сегмент, на высоту сегмента. Следовательно, площадь 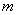 -й зоны будет равна:
-й зоны будет равна:
 . .
| (3.6) |
Полученное выражение не зависит от m. Это означает, что при принятых допущениях площади зон Френеля примерно одинаковы.
Из равенства (3.3) легко найти радиусы этих зон. Высота сегмента 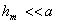 , поэтому можно считать, что
, поэтому можно считать, что 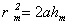 . Подставив значение (3.5) для
. Подставив значение (3.5) для  , получим, что радиус внешней границы
, получим, что радиус внешней границы 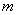 -й зоны равен:
-й зоны равен:
 . .
| (3.7) |
Так как расстояние от зоны до точки Р медленно растет с увеличением номера зоны m, и угол j между нормалью к элементам зоны и направлением на точку Р также растет, то амплитуда колебания, возбуждаемого зонами Френеля в точке Р, монотонно убывает с ростом номера зоны. Даже при очень больших 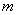 , когда площадь зоны начинает заметно расти с увеличением
, когда площадь зоны начинает заметно расти с увеличением 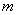 , убывание множителя
, убывание множителя  перевешивает рост
перевешивает рост 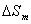 , так что амплитуда продолжает убывать. В результате амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, монотонно убывают:
, так что амплитуда продолжает убывать. В результате амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, монотонно убывают: 
Фазы колебаний, возбуждаемых соседними зонами, отличаются на  . Поэтому амплитуда результирующего колебания в точке Р может быть представлена в виде
. Поэтому амплитуда результирующего колебания в точке Р может быть представлена в виде

| (3.8) |
В это выражение все амплитуды от нечетных зон входят с одним знаком, а от четных – с другим. Сгруппируем члены в (3.8) следующим образом:
 , ,
| (3.9) |
при последнем члене будет знак плюс, если число зон нечетное, знак минус – при четном числе зон. Вследствие монотонного убывания амплитуды приближенно можно считать, что  . Тогда выражения в скобках равны нулю. При полностью открытом фронте последний член суммы стремится к нулю, так как
. Тогда выражения в скобках равны нулю. При полностью открытом фронте последний член суммы стремится к нулю, так как  . Поэтому
. Поэтому
 . .
| (3.10) |
Таким образом, при свободном распространении волны волновое возмущение в точке Р от всего фронта составляет половину возмущения, даваемого только одной первой зоной Френеля. Амплитуда результирующего колебания, получающегося вследствие взаимной интерференции волн, идущих к точке Р от различных участков сферической волны, меньше амплитуды, создаваемой действием центральной зоны. Действие всей волны на точку Р сводится к действию ее малого участка, меньше, чем центральная зона с площадью  .
.
Оценим размеры зон Френеля. Длина световой волны очень мала,  . Поэтому для расстояния
. Поэтому для расстояния  , примерно равного 1 м, площадь действующей части волны меньше 1 мм 2. Следовательно, распространение света от источника
, примерно равного 1 м, площадь действующей части волны меньше 1 мм 2. Следовательно, распространение света от источника  к точке Р происходит так, как если бы световой поток шел внутри очень узкого канала вдоль
к точке Р происходит так, как если бы световой поток шел внутри очень узкого канала вдоль  , то есть прямолинейно.
, то есть прямолинейно.
Хорошей иллюстрацией, подтверждающей рассуждения Френеля, может служить опыт с зонной пластинкой. Зонная пластинка представляет собой экран, состоящий из последовательности чередующихся прозрачных и непрозрачных колец, радиусы которых при выбранных значениях a, b и l удовлетворяют соотношению  . Приготовленный таким образом экран называется амплитудной зонной пластинкой.
. Приготовленный таким образом экран называется амплитудной зонной пластинкой.
Если расположить такую пластинку на расстоянии  от точечного источника и на расстоянии
от точечного источника и на расстоянии  от точки наблюдения на линии, соединяющей эти две точки, то для длины волны
от точки наблюдения на линии, соединяющей эти две точки, то для длины волны  пластинка прикроет все четные зоны и оставит свободными все нечетные, начиная с центральной. Тогда амплитуда результирующего колебания в точке Р определится соотношением
пластинка прикроет все четные зоны и оставит свободными все нечетные, начиная с центральной. Тогда амплитуда результирующего колебания в точке Р определится соотношением  , то есть окажется значительно больше, чем при полностью открытом фронте. Усиление интенсивности света зонной пластинкой эквивалентно фокусирующему действию собирающей линзы.
, то есть окажется значительно больше, чем при полностью открытом фронте. Усиление интенсивности света зонной пластинкой эквивалентно фокусирующему действию собирающей линзы.
Ещё большего эффекта можно добиться, не перекрывая зоны, а изменяя их фазу на π. В этом случае  . Впервые это было осуществлено Робертом Вудом.. Он покрыл стекло тонким слоем лака и выгравировал на нем зонную пластинку так, что оптическая толщина нечетных зон отличалась от толщины четных зон на
. Впервые это было осуществлено Робертом Вудом.. Он покрыл стекло тонким слоем лака и выгравировал на нем зонную пластинку так, что оптическая толщина нечетных зон отличалась от толщины четных зон на  . Такие пластинки называют фазовыми зонными пластинками.
. Такие пластинки называют фазовыми зонными пластинками.
Зонные пластинки, так называемые линзы Френеля, находят применение не только в оптике, но и в акустике и радиотехнике для достаточно малых длин волн, при которых размеры линз получаются не слишком большими (сантиметровые радиоволны, ультразвуковые волны).
3.4. Графическое вычисление результирующей амплитуды.
Спираль Френеля
Рассмотрение вопроса о действии световой волны в точке Р удобно проводить, пользуясь графическим методом сложения колебаний, обладающих некоторой разностью фаз. Известно, что любое колебание можно представить вектором, модуль которого равен амплитуде колебания, а угол, который вектор составляет с заранее выбранным направлением, равен фазе колебания. При сложении нескольких колебаний, изображаемых с помощью векторов, суммарное колебание определяется по правилу сложения векторов.
Совершенно очевидно, что для каждой зоны Френеля фаза будет плавно меняться от границы начала зоны до её конца. Однако с каждой зоной можно поступить как со всей поверхностью фронта. Разобьем каждую зону Френеля на кольцевые подзоны, аналогичные зонам Френеля, но гораздо меньшие по ширине, чтобы фаза колебаний, вызываемых в точке  различными источниками вторичных волн такой подзоны, практически могла считаться постоянной. Тогда действие каждой подзоны можно представить вектором, длина которого дает суммарную амплитуду, а направление определяет фазу колебания, обусловленного этой подзоной. Действие соседней подзоны можно выразить вторым вектором, несколько повернутым относительно первого, так как фаза, определяемая совокупностью источников этой подзоны, будет немного отличаться от фазы, задаваемой первой подзоной. По длине же этот вектор практически не будет отличаться от первого, так как амплитуда колебания, вызываемого различными участками фронта волны, отличается только вследствие изменения наклона нормали к фронту волны к линии, проведенной в точку Р, а для двух соседних зон это изменение ничтожно мало.
различными источниками вторичных волн такой подзоны, практически могла считаться постоянной. Тогда действие каждой подзоны можно представить вектором, длина которого дает суммарную амплитуду, а направление определяет фазу колебания, обусловленного этой подзоной. Действие соседней подзоны можно выразить вторым вектором, несколько повернутым относительно первого, так как фаза, определяемая совокупностью источников этой подзоны, будет немного отличаться от фазы, задаваемой первой подзоной. По длине же этот вектор практически не будет отличаться от первого, так как амплитуда колебания, вызываемого различными участками фронта волны, отличается только вследствие изменения наклона нормали к фронту волны к линии, проведенной в точку Р, а для двух соседних зон это изменение ничтожно мало.

 Таким образом, векторная диаграмма, определяющая действие подзон, составляющих первую зону Френеля, изобразится ломаной линией (рис. 3.8). Если площадь подзон уменьшать, то ломаная линия превратится в дугу, которая очень мало будет отличаться от полуокружности (рис. 3.9). При этом вектор, касательный к дуге в точке
Таким образом, векторная диаграмма, определяющая действие подзон, составляющих первую зону Френеля, изобразится ломаной линией (рис. 3.8). Если площадь подзон уменьшать, то ломаная линия превратится в дугу, которая очень мало будет отличаться от полуокружности (рис. 3.9). При этом вектор, касательный к дуге в точке  , будет иметь направление, прямо противоположное направлению соответствующего вектора вблизи точки О, так как фаза колебания в точке Р, обусловленного действием последней подзоны, очевидно, противоположна фазе колебаний, излучаемых первой подзоной. Таким образом, результирующее колебание, обусловленное действием одной центральной зоны, представится вектором длиной
, будет иметь направление, прямо противоположное направлению соответствующего вектора вблизи точки О, так как фаза колебания в точке Р, обусловленного действием последней подзоны, очевидно, противоположна фазе колебаний, излучаемых первой подзоной. Таким образом, результирующее колебание, обусловленное действием одной центральной зоны, представится вектором длиной  .
.
Для того чтобы учесть действие второй зоны Френеля, надо продолжить векторную диаграмму. Тогда мы получим картину, представленную на рис. 3.10. Причем дуга  короче дуги
короче дуги  вследствие возрастающего наклона зоны. Результирующий вектор от второй зоны Френеля направлен противоположно вектору первой зоны, но немного меньше его по модулю, поэтому их сумма не будет точным нулем, а даст небольшой суммарный вектор в нижней части рис. 3.10.
вследствие возрастающего наклона зоны. Результирующий вектор от второй зоны Френеля направлен противоположно вектору первой зоны, но немного меньше его по модулю, поэтому их сумма не будет точным нулем, а даст небольшой суммарный вектор в нижней части рис. 3.10.
 Рис. 3.11
Рис. 3.11
|
Продолжая построение, получим диаграмму действий всей волны в виде спирали, закручивающейся к точке С (рис. 3.11). Результирующее колебание, характеризующее действие всего волнового фронта, выражается вектором длиной ОС. Из рис. 3.11 легко видеть, что этот вектор равен примерно половине длины вектора  , представляющего действие первой зоны Френеля, и совпадает с ним по направлению. Другими словами, колебание в точке
, представляющего действие первой зоны Френеля, и совпадает с ним по направлению. Другими словами, колебание в точке  , обусловленное действием всего волнового фронта, совпадает по фазе с колебанием, которое могла бы создать центральная зона, а его амплитуда составляет примерно половину амплитуды этого колебания.
, обусловленное действием всего волнового фронта, совпадает по фазе с колебанием, которое могла бы создать центральная зона, а его амплитуда составляет примерно половину амплитуды этого колебания.
Приведенные рассуждения показывают, что действие (то есть амплитуда), вызванное всем волновым фронтом, примерно равно половине действия центральной зоны, а не действию половины центральной зоны. Действие половины центральной зоны выражается вектором  , отличающимся от вектора
, отличающимся от вектора  (рис. 3.11).
(рис. 3.11).
Не нашли, что искали? Воспользуйтесь поиском: