Работа 3. Цепь переменного синусоидального тока с последовательным соединением катушки и конденсатора. Резонанс напряжений.

Цель работы: изучить явления, происходящие в неразветвленных цепях переменного синусоидального тока при изменении соотношений величин индуктивности и емкости; ознакомиться с явлением резонанса напряжений.

Пояснения к работе

Рассмотрим процессы в цепи с последовательным соединением катушки и конденсатора (рис. 3.1).

Рис.3.1. Схема цепи с последовательным соединением

катушки и конденсатора

Реальная катушка обладает индуктивным сопротивлением x_L=wL и активным сопротивлением r = r , где w – угловая частота переменного тока, L – индуктивность катушки, r – удельное электрическое сопротивление провода катушки, l – длина провода, S – площадь поперечного сечения провода. При прохождении тока через катушку, электрическая энергия расходуется на нагревание провода катушки. Скорость преобразования электрической энергии в тепловую учитывается с помощью величины, называемой активной мощностью P = rI². Измерив ток и активную мощность катушки, можно вычислить активное сопротивление катушки . Его можно определить также, пропуская через катушку постоянный ток. В цепи постоянного тока катушка обладает только активным сопротивлением, так как угловая частота w=2p¦=0 и x_L = wL=0. Поэтому , где U – постоянное напряжение, приложенное к катушке, а I – сила постоянного тока, протекающего через катушку.

Эквивалентная схема замещения катушки может быть представлена в виде последовательного соединения резистивного и индуктивного идеальных элементов (рис. 3.2).

Рис.3.2. Эквивалентная схема замещения катушки

Напряжение на катушке U_к можно разложить на две составляющие – активную U_ак и индуктивную U_L Векторная диаграмма напряжений и тока для катушки приведена на рис. 3.3.

Напряжение U_к можно измерить на выводах катушки с помощью вольтметра, ток I – с помощью амперметра. Угол сдвига фаз между током и напряжением катушки j_к можно определить из формулы P_к = U_к I cosj_к, если измерить с помощью ваттметра активную мощность катушки P_к. Составляющие напряжения U_к, U_L и U_ак можно вычислить из треугольника напряжений ОАВ (рис.3.3): U_ак=U_кcosj_к или определить графически, опустив перпендикуляр из конца вектора U_к (точка А на рис. 3.3) на линию вектора I.

Рис.3.3. Векторная диаграмма напряжения и тока для катушки

Конденсатор в цепи переменного тока обладает емкостным сопротивлением , где C – емкость конденсатора. Следует указать, что в конденсаторе также имеются активные потери энергии в диэлектрике. Однако величина этих потерь настолько мала, что ими можно пренебречь. На схеме замещения конденсатор можно представит в виде идеального емкостного элемента с параметром С, равным емкости конденсатора.

Последовательное соединение катушки и конденсатора изображено в виде схемы замещения на рис. 3.4.

Рис.3.4. Схема замещения цепи с последовательным

соединением катушки и коденсатора

При подключении такой цепи под напряжение U в ней возникает ток I.

Вектор активной составляющей напряжений на катушке будет совпадать по направлению с вектором тока İ (рис.3.5), так как соответствующие синусоиды мгновенных значений совпадают по фазе:

i = I_msinwt и U = i r =I_m r sinwt. (3.1)

Вектор индуктивного напряжения =İх_L опережает по фазе вектор тока İ на (рис. 3.6), так как синусоида напряжения U_L на индуктивности опережает по фазе синусоиду тока i на .

U_L = L = I_mwt sin(wt + 90˚). (3.2)

Вектор емкостного напряжения =İх_C отстает по фазе от вектора тока İ на (рис. 3.7), так как синусоида напряжения на емкости при нулевых начальных условиях отстает от синусоиды тока i на .

. (3.3)

Рис.3.5. Векторная диаграмма напряжения и тока

при активной нагрузке цепи.

Рис. 3.6. Векторная диаграмма напряжения и тока

при индуктивной нагрузке цепи

Рис. 3.7. Векторная диаграмма напряжения и тока

при емкостной нагрузке цепи

Для рассматриваемой цепи уравнений по второму закону Кирхгофа имеет следующий вид:

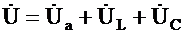, (3.4)

где

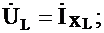
Согласно уравнению (3.4) и рис.3.5 – 3.7, векторная диаграмма напряжений цепи (рис.3.4) будет иметь вид, показанный на рис. 3.8, где вектор совпадает по фазе с вектором İ, а вектор опережает по фазе на 90˚ вектор тока İ. Сумма векторов и дает вектор напряжения катушки:

,

Опережающий по фазе ток на угол j_к.

Вектор отстает по фазе на 90˚ от вектора тока İ. Сумма векторов _{, ,} дает вектор напряжения сети , опережающий ток по фазе на угол j.

Разделив и умножив стороны треугольника (рис.3.8) на величину тока İ, получим подобные треугольники сопротивлений и мощностей (рис.3.9, 3.10).

Из треугольника сопротивлений (см. рис.3.9) найдем полное сопротивление Z и cosj цепи

Z= . (3.5)

cosj = . (3.6)

Рис. 3.8. Векторная диаграмма тока и напряжений

для цепи с последовательным соединением

элементов r, L, C при x_L>x_C

Рис. 3.9. Треугольник сопротивлений для цепи с последовательным

соединением элементов r, L, C.

Из векторной диаграммы напряжений (см.рис.3.8) получим формулу тока I, которая является выражением закон Ома для последовательной цепи переменного тока:

. (3.7)

Из диаграммы мощностей (рис.3.10) получим соотношение между полной S, активной P и реактивными Q_L и Q_c мощностями

. (3.8)

Рис. 3.10. Треугольник мощностей для цепи с последовательным

соединением элементов r, L, C.

Изменяя величину емкости в цепи, можно изменять соотношение между емкостными и индуктивными сопротивлениями и напряжениями:

и U_L=I ω L

и получать различные значения угла сдвига φ между вектором тока İ и вектора напряжения сети согласно уравнению (3.6). Если величина L> имеем: ωL> и U_L>U_C, т.е. в цепи преобладает индуктивное сопротивление x_L и напряжение , поэтому вектор тока İ отстает по фазе от вектора напряжение сети на угол φ (см.рис. 3.8).

Если L< , наоборот, преобладает емкостное сопротивление x_C и напряжение , поэтому вектор тока İ опережает по фазе вектор напряжения сети (рис. 3.11).

Рис. 3.11. Векторная диаграмма тока и напряжений

для цепи с последовательным соединением

элементов r, L, C при x_L<x_C

При величине индуктивности

(3.9)

индуктивное сопротивление будет равно емкостному:

(3.10)

а, следовательно, будут равны между собою индуктивное и емкостное напряжения (рис. 3.12).

Ix_L=Ix_С; U_L=U_C. (3.11)

Мы получим резонанс напряжения, т.е. полную взаимную компенсацию индуктивного и емкостного напряжений:

При резонансе напряжений угол сдвига φ=0, следовательно:

cos φ=1 (3.12)

Вектор напряжения (рис. 3.12).

Полное сопротивление цепи при резонансе z_рез принимает минимальное значение z_рез= r, так как x_L-x_C=0, а, следовательно, ток при резонансе I_рез и активная мощность принимают максимальные значения:

,

(3.13)

Рис. 3.12. Векторная диаграмма тока и напряжений

при резонансе напряжений (x_L= x_C)

Реактивная мощность равна нулю

Q = I(U_L-U_C)= 0; Q_L-Q_C=0. (3.14)

Индуктивное U_L и емкостное U_C напряжения в раз больше напряжения сети U:

Поэтому резонанс напряжений может оказаться опасным для установки. При испытании таких цепей требуется особая осторожность. Явление резонанса напряжений, т.е. взаимной компенсации реактивных напряжений (U_L-U_C= 0), а последовательно, и реактивных мощностей (Q_L-Q_C) объясняется тем, что мгновенные значения напряжений на индуктивности U_L и на емкости U_C в любой момент времени равны и имеют противоположные знаки. Отсюда следует, что если, например, индуктивность берет энергию из сети для создания магнитного поля, то в этот момент конденсатор, разряжаясь, отдает энергию в сеть.

Происходит взаимная компенсация энергии, потребляемой ими из сети.

Таким образом, при резонансе полная энергия, потребляемая из сети, расходуется только на нагревание резисторного элемента цепи.

Кривые зависимости Z сопротивления цепи от величины емкости С показаны на рис. 3.13. При величина Z минимальна и равна Z_рез= r.

На рис. 3.13 показана также кривая зависимости тока I и cosφ от величины емкости C. При C= C_рез ток I имеет максимальное значение , при всех других значениях емкости

Рис. 3.13. Графика зависимости полного сопротивления цепи Z

тока I и коэффициента мощности cosφ от емкости,

(при L= const)

Из выражения (3.10) видно, что резонанс напряжений в цепи может быть получен изменением индуктивности L или емкости C при неизменной частоте сети f или изменением частоты сети при заданных постоянных L и C.

Построение векторных диаграмм.

При последовательном соединении элементов цепи через каждый из них протекает один и тот же ток I. Поэтому при построении векторных диаграмм для таких цепей вектор тока принимается за базовый (исходный). Векторные диаграммы строят циркулем методом засечек по известным из опыта напряжениям: U_a – на зажимах резистора, U_к – на зажимах катушки, U_с – на зажимах конденсатора и U – на зажимах всей цепи. Все величины на диаграммах изображаются в масштабе.

В качестве примера рассмотрим построение векторной диаграммы для цепи с последовательным соединением резистора (реостата) и катушки. Напряжение на резисторе U_a, совпадающее по фазе с током I, откладывают в масштабе по линии тока. Из конца вектора радиусом, равным напряжению на катушке U_к, делают первую засечку. Вторая засечка делается радиусом, равным общему напряжению цепи U из начала вектора . В точке пересечения засечек будут находиться концы векторов и (рис. 3.14.а). Активную и индуктивную составляющую напряжений на катушке и определяют, опуская перпендикуляр на ось вектора тока İ из конца вектора .

Векторная диаграмма для цепи с последовательным соединением катушки и конденсатора, строится аналогично и приведена на рис. 3.14.б.

а б

Рис. 3.14. Построение векторных диаграмм методом засечек.

Рис. 3.15. Схема соединений электрической цепи с последовательным

включением катушки и батареи конденсаторов.

Порядок выполнения работы.

1. Собрать электрическую цепь по схеме рис. 3.15.

2. Произвести исследование явления резонанса напряжений по следующей методике.

Изменяя величину емкости включением тумблеров, установить емкость С₀, при которой ток в цепи I и активная мощность P имеют максимальные значения (явление близкое к резонансу напряжений). Произвести измерения напряжения U в цепи, напряжения на катушке U_к, напряжения на конденсаторе U_с, тока I в цепи и мощности P. Изменяя затем емкость ступенями на 1 – 2 мкф, произвести измерения для 3 – 4 точек при емкостях, меньших С₀, и для 3 – 4 точек при емкостях, больших С₀.

3. Результаты измерений для каждой установленной величины емкости занести в табл.3.1.

Таблица 3.1

4. По данным опытов вычислить величины, указанные в табл. 3.1 (полное сопротивление цепи Z, активное сопротивление r, реактивное сопротивление x, коэффициент мощности цепи cosφ, емкостное сопротивление x_C, емкость C, полное сопротивление катушки z_к, индуктивное сопротивление катушки z_L, индуктивность катушки L, коэффициент мощности cosφ_к).

Формулы для вычислений

; ; ; ;

; ; ;

;

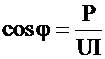5. По данным табл. 3.1 построить кривые I=f₁(C), cosφ=f₂(С); z=f₃(С).

6. Построить векторные диаграммы тока и напряжений для трех отсчетов: при x_L>x_C, при максимальном значении тока в цепи (x_L≈x_C), при x_L<x_C.

Контрольные вопросы:

1. Что называется индуктивным и емкостным сопротивлением и от чего они зависят?

2. Как вычисляется полное сопротивление неразветвленной цепи переменного тока?

3. Как вычисляется действующее значение тока в цепи с последовательным соединением резистивного, индуктивного и емкостного элементов?

4. Что такое коэффициент мощности цепи переменного тока и почему нужно стремиться к его повышению при потреблении электрической энергии?

5. При каком условии возникает резонанс напряжений в цепи переменного синусоидального тока? Чем характеризуется это явление?

6. Объясните, какую опасность может представлять резонанс напряжений в электрических цепях?

7. Каким должно быть соотношение индуктивного и емкостного сопротивлений, чтобы ток в цепи опережал напряжение? Поясните это при помощи векторной диаграммы.

8. Начертите схему замещения цепи, для которой изображена векторная диаграмма.

Что нужно дополнительно включить в эту цепь, чтобы получить в ней резонанс напряжений?

9. В цепи переменного тока частотой f=50 Гц с последовательно включенными катушкой и конденсатором имеет место резонанс. Определить напряжение на катушке и конденсаторе, если U=20В, r=10Ом, c=1мкФ. Вычислить индуктивность катушки.

Не нашли, что искали? Воспользуйтесь поиском: