Работа 4. Параллельное соединение индуктивности и емкости.

Резонанс токов.

Цель работы: рассмотреть явления, происходящие в цепи переменного тока, содержащей параллельно соединенные катушку и конденсатор (рис. 4.1), ознакомиться с резонансом токов.

Рис. 4.1. Схема электрической цепи с параллельным

соединением элементов.

Пояснения к работе

Рассмотрим параллельное соединение катушки, обладающей индуктивным x_L=ωL и активным r сопротивлениями, с конденсатором, обладающим емкостным сопротивлением (рис. 4.2). При включении такой цепи под напряжением U в катушке возникает ток I_к.

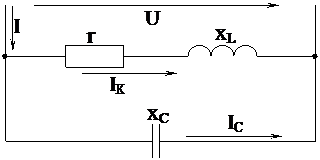
Рис. 4.2. Принципиальная схема параллельного

соединения r, x_L, x_c

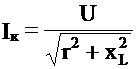, (4.1)

где 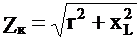— полное сопротивление катушки.

Вектор тока будет отставать от вектора напряжения на угол φ_к:

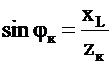; . (4.2)

В конденсаторе возникает ток I_c:

. (4.3)

Вектор тока İ_c будет опережать на 90˚ вектор , φ_с= 90˚. Вектор общего тока на основании первого закона Кирхгофа:

İ = İ_к + İ_с. (4.4)

Векторная диаграмма токов согласно (4.4) показана на рис.4.З

Вектор тока İ_к проводим под углом φ_к к вектору напряжения . Из конца вектора тока İ_к проводим вектор тока İ_с под углом φ_с=90˚ к вектору напряжения (в сторону опережения). Сумма вектора İ_к и İ_с даст вектор общего тока, отстающий на угол φ от вектора напряжения.

Для аналитического определения общего тока I и угла φ разложим ток катушки I_к на активную составляющую I_a, совпадающую с напряжением U, и индуктивностью I_L, отстающую на 90˚ от напряжения U.

;

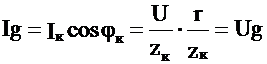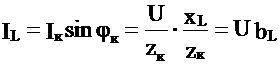, (4.5)

где g и b_L – активная и индуктивная проводимости катушки:

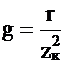; . (4.6)

Аналогично определяются проводимости конденсатора. При отсутствии в конденсаторе активного сопротивления (r_c= 0) активная проводимость его равна нулю: , где z_c= x_c.

Емкостная проводимость:

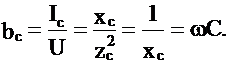(4.7)

Из векторной диаграммы на рис. 4.3. имеем:

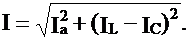(4.8)

. (4.9)

Подставим значения I_a, I_L и I_c из уравнения (4.5) и (4.7) в уравнение (4.8), получим:

. (4.10)

где 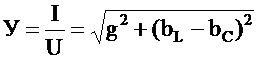– полная проводимость всей цепи.

Разделив стороны треугольника (рис.4.3) на напряжение U, получим треугольник проводимостей (рис.4.4), из которого находим:

(4.11)

Изменяя величину емкости С, от которой зависит значение b_c, согласно (4.7), можно изменять соотношение между b_c и индуктивными проводимостями (b_L), а, следовательно, и токами:

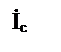I_c=Ub_c=Uωс; I_L=Ub_L

Рис.4.3. Векторная диаграмма напряжения и токов для цепи с параллельным

соединением катушки и емкости при I_L>I_С

При величине b_C<b_L, т.е. C< 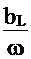имеем:

Uωс<Ub_c или I_C<I_L.

Преобладает индуктивная проводимость b_L и, следовательно, ток I_L, поэтому вектор общего тока İ отстает от вектора напряжения (рис.4.3).

При величине b_C>b_L, т.е. C> 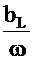имеем:

Uωс<Ub_L или I_L<I_С

Преобладает емкостная проводимость b_C и, следовательно, ток I_С, поэтому вектор общего тока İ опережает вектор напряжения (рис.4.5).

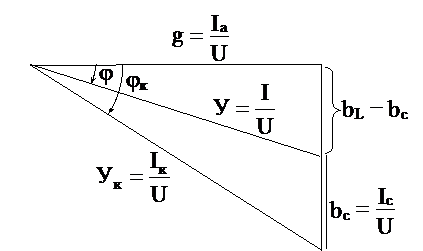
Рис.4.4. Векторная диаграмма для цепи с параллельным

соединением катушки и емкости при I_C< I_L

Рис.4.5. Векторная диаграмма для цепи с параллельным

соединением катушки и емкости при I_C> I_L

При величине емкости: , (4.12)

емкостная проводимость равна индуктивной:

b_C = ωc = b_L, (4.13)

а, следовательно, будут равны между собою емкостный и индуктивный токи (рис.4.6):

b_C U= b_LU; I_C= I_L. (4.14)

Мы получим резонанс токов, т.е. полную взаимную компенсацию индуктивного и емкостного токов:

I_C – I_L= 0. (4.15)

В результате общий ток I при резонансе состоит только из активной составляющей, согласно выражению (4.8) и рис.4.6.

I= I_a= Ug, (4.16)

поэтому угол φ= 0, а cos φ= 1.

Полная проводимость цепи, а следовательно, и ток I принимает минимальное значение, так как согласно (4.10) У=g, поскольку b_C – b_L= 0, а полное сопротивление цепи 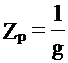, следовательно максимальное значение.

Реактивная мощность цепи равна нулю:

U(I_C - I_L) = 0; Q_L – Q_C= 0.

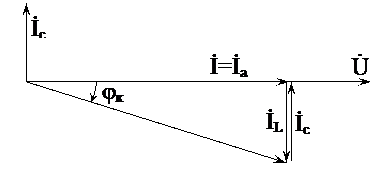Рис.4.6. Векторная диаграмма при резонансе токов (I_C= I_L)

Явление резонанса токов, т.е. взаимной компенсации реактивных токов (I_C–I_L=0), а, следовательно, и реактивных мощностей (Q_L–Q_C=0) объясняют следующим. Когда индуктивная ветвь (катушка) потребляет энергию для создания магнитного поля, в этот момент в параллельной ветви конденсатор разряжается и отдает энергию. Происходит взаимная компенсация энергий.

Общая энергия, потребляемая из сети, расходуется только на активном сопротивлении катушки (на нагревание провода катушки).

Зависимость полного сопротивления Z цепи от величины емкости будет иметь следующий вид:

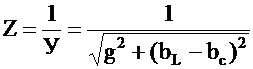, (4.18)

где 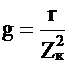и 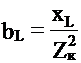от C не зависят.

Кривые Z= f₁(C) и I= f₂(C), построенные по выражениям (4.18) и (4.10), показаны на рис.4.7. Там же дана кривая cosφ= f₃(C), построенная по уравнению (4.11). Из (4.12) видно, что величины емкости и индуктивности, при которых наступает резонанс, зависят от частоты переменного тока. При заданных постоянных C и L явление резонанса может быть получено изменением частоты.

Рис.4.7. График зависимости тока в цепи I, cosφ

и полного сопротивления z от емкости.

Не нашли, что искали? Воспользуйтесь поиском: