Краткие сведения из теории. Простейший электрический колебательный контур состоит из конденсатора и катушки индуктивности, соединенных между собой (Рис

Простейший электрический колебательный контур состоит из конденсатора и катушки индуктивности, соединенных между собой (Рис. 1). Для простоты можно считать, что емкость между витками катушки и индуктивность соединительных проводов малы, т.е. вся емкость сосредоточена в конденсаторе, а индуктивность – в катушке.

Допустим, что при разомкнутом ключе конденсатор зарядили до напряжения U ₀ (сообщили заряд Q ₀). Энергия электрического поля равна:

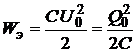После замыкания ключа начинается процесс разрядки конденсатора через катушку, в которой возникает ЭДС самоиндукции, препятствующая разрядному току. В катушке появляется магнитное поле, которое становится максимальным при полной разрядке конденсатора Энергия электрического поля преобразуется в энергию магнитного поля:

.

Далее ток начинает уменьшаться, возникает ЭДС самоиндукции, теперь поддерживающая уменьшающийся ток разряда. Конденсатор перезарядится до первоначального напряжения, но электрическое поле будет противоположного направления. Произойдет обратное преобразование энергии магнитного поля в энергию электрического поля. В дальнейшем процессы будут повторяться в обратном направлении, и в конечном итоге колебательная система вернется в исходное состояние. Если активное сопротивление колебательного контура R равно нулю, описанные выше колебания называются собственными электрическими колебаниями.

Период собственных колебаний определяется по формуле

,

а частота и циклическая (круговая) частоты, соответственно, равны:

.

Величина w ₀ называется собственной частотой колебательного контура.

В замкнутом колебательном контуре (Рис. 2), включающем в себя сопротивление R, индуктивность L и емкость C, по второму закону Кирхгофа сумма падений напряжения равна сумме ЭДС:

,

а, выразив напряжение на конденсаторе и ток в контуре через заряд

,

получаем дифференциальное уравнение второго порядка, связывающее заряд на обкладках конденсатора со временем:

.

Поделив на L и введя обозначения и , получаем окончательное уравнение:

.

При отсутствии активного сопротивления R это уравнение упрощается:

,

и его решением являются уравнения гармонических колебаний заряда, напряжения на конденсаторе и силы тока в контуре

.

,

где , а график колебаний представляет собой косинусоиду с плавно уменьшающейся амплитудой (Рис. 3).

Показатель b называется коэффициентом затухания, и его можно определить из следующего отношения последующих амплитуд:

.

Логарифм этого отношения называется логарифмическим декрементом затухания и равен:

,

где – период затухающих колебаний. Логарифмический декремент затухания можно определить и другим способом. Если обозначить t время, за которое амплитуда колебаний уменьшится в e раз, то

,

а, следовательно,

,

и отсюда получаем формулу для экспериментального определения d

.

.

Описанные выше рассуждения верны для небольших сопротивлений R, т.е. при которых выполняется условие . Если же сопротивление велико, и то электрических колебаний в контуре не возникает вовсе, а напряжение на конденсаторе по экспоненте спадает до нуля. Это происходит, при сопротивлениях, больших критического сопротивления R_кр, удовлетворяющего условию:

.

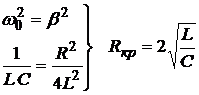Не нашли, что искали? Воспользуйтесь поиском: