Краткие сведения из теории. Переменным током называется любой ток, величина которого периодически меняется со временем

Переменным током называется любой ток, величина которого периодически меняется со временем. Но чаще всего под переменным током подразумевается ток, меняющийся по закону синуса (или косинуса):

,

где I – амплитуда тока, – циклическая частота, а – фаза колебаний, характеризующая состояние колебательной системы в данный момент времени t.

Рассмотрим электрическую цепь, содержащую последовательно соединенные резистор, конденсатор и катушку индуктивности, подключенную к источнику переменного напряжения (Рис. 1). По этой цепи протекает ток, меняющийся по синусоидальному закону

.

,

но при переменном токе в цепи, содержащей емкость и индуктивность, есть некоторые отличия.

Падение напряжения на резисторе колеблется по такому же закону, как и ток

,

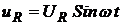и их фазы колебаний совпадают.

Напряжение на обкладках конденсатора пропорционально заряду на них в каждый момент времени

,

а заряд можно определить как интеграл тока по времени

.

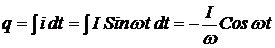Тогда

.

Из этого выражения следуют два вывода: во-первых, колебания напряжения на конденсаторе отстают от колебаний тока на 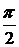, а во-вторых, амплитудное значение напряжение связано с амплитудным значением тока соотношением:

,

где называется емкостным сопротивлением.

.

В этом случае для участка цепи, содержащего катушку (т.е. источник ЭДС, включенный навстречу току) падение напряжения равно

,

так как помимо ЭДС самоиндукции происходит падение напряжения на сопротивлении провода r, из которого изготовлена катушка. Если предположить его малым, то и

.

Очевидно, что колебания напряжения на катушке опережают колебания тока на 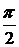, а их амплитуды связаны соотношением

,

где – индуктивное сопротивление катушки.

Сопротивления R, r называются активными (или омическими), а сопротивления X_L и X_C – реактивными.

Соотношения фаз колебаний напряжений на активных и реактивных сопротивлениях можно проиллюстрировать на векторной диаграмме (Рис. 2). За основное направление надо взять силу тока, так как он является общим для последовательно соединенных элементов схемы. Величину амплитуды выходного напряжения можно определить, используя закон сложения векторов:

Видно, что колебания напряжения и тока сдвинуты по фазе друг относительно друга на j. Вынеся общий множитель – силу тока – из-под корня, получаем выражение:

,

где R ₀ – все активное сопротивление электрической цепи. Это выражение является математической формулировкой закона Ома для переменной цепи. Общее сопротивление цепи Z и тангенс сдвига фаз между колебаниями тока и напряжения tgj определяется по формулам:

.

Как видно из этих формул, полное сопротивление цепи переменного тока зависит не только от величин активного сопротивления, индуктивности и емкости, но и от частоты переменного тока. При частоте близкой к нулю полное сопротивление цепи определяется емкостным сопротивлением 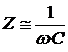и стремится к бесконечности, а сдвиг фаз . При высокой частоте переменного тока соответственно и .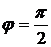

Интересная ситуация наблюдается, когда частота переменного тока удовлетворяет условию:

.

Интересен также факт превышения напряжения на реактивных элементах схемы выходного напряжения источника тока. Если в момент резонанса индуктивное и емкостное сопротивления больше активного сопротивления цепи , то напряжения на них .

Не нашли, что искали? Воспользуйтесь поиском: