ОСНОВЫ ТЕОРИИ ПОГРЕШНОСТЕЙ

3.I. Элементы математической статистики

Пусть в некотором эксперименте проведено N измерений неко­торой величины X. Получены значения величины X, которые в общем случае отличаются друг от друга:

X₁; X₂;... X_i,... X_N (3)

Если , то говорят о полном наборе величин X или о генеральной совокупности. Реально N невелико, эксперимен­татор имеет дело с неполным набором величин X, который называется выборкой из генеральной совокупности.

Величина

(4)

называется средним арифметическим (средним выборочным) значением измеряемой величины X.

Разность (5)
называется случайным отклонением i -го измерения от среднего, или абсолютной погрешностью отдельного измерения. Можно ввести среднюю абсолютную погрешность измерений

(6)

В основе теории погрешностей лежат положения, сформулирован­ные Гауссом:

- погрешности равной абсолютной величины и противоположных знаков
равновероятны (эto означает, что если в генеральной совокупности
есть значение X+Δ_i, то можно утверждать, что с той же
вероятностью совокупность содержит значение X - Δ_i);

- чем больше абсолютная погрешность, тем она менее вероятна.

С учётом этих положений можно утверждать, что если , то средняя абсолютная погрешность стремится к нулю и среднее арифме­тическое значение измеряемой величины стремится к истинному зна­чению. Отсюда следует вывод, что для повышения точности измерений необходимо увеличивать число измерений N.

Результаты измерений (3) можно представить наглядно, построив диаграмму, которая показывает частоту (вероятность) получения тех или иных значений измеряемой величины в серии (3). Такую диаг­рамму называют гистограммой и строят её следующим образом (рис.1). Весь диапазон изменения измеряемой величины в серии (3) разобьём на некоторое число одинаковых интервалов и отложим их на оси абсцисс. На этих интервалах построим прямоугольники с высотой, равной , где - число результатов в серии (3), попавших в m -й интервал. Площади прямоугольников имеют смысл вероятности получения результата из соответствующего интервала оси абсцисс.

Рис.1. Рис.2.

Если измеряемая величина X меняется непрерывно в интервале , а число измерений N неограниченно возрастает, то при ,стремящемся к нулю, гистограмма, представленная на рис.1, перейдет в плавную кривую p(x), которую называют плотностью распределения вероятности результатов измерения (рис.2). Произведение равно вероятности получения результата из интервала [ X,X+dX ]:

(7)

Вероятность получения результата измерения из некоторого конечного
интервала [ X₁,X₂ ] равна площади под кривой p(X) в заданном интервале:

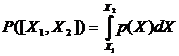(8)

Очевидно, что площадь под всей кривой p(x), как вероятность
достоверного события, равна:

(9)

В случае, если отклонение измеряемых величин в серии (3) обусловлены случайной погрешностью, то, как показывает опыт, плотность распределения вероятности результатов при большом числе измерений хорошо описывается функцией:

, (10)

которая называется нормальной (или гауссовой) плотностью распре­деления вероятности.

График функции (10) представлен на рис.2. Видно, что при функция имеет максимум. Это означает, что чем меньше абсо­лютная погрешность отдельного измерения, тем она более вероятна.

Параметр σ в выражении (10) называется среднеквадратичным отклонением результатов измерения (среднеквадратичной погрешностью отдельного измерения) и характеризует степень разброса результа­тов измерения относительно среднего арифметического. Величину σ² называют дисперсией результатов измерения. Чем больше σ, тем шире распределение (10) и тем больше вероятность заметных откло­нений результатов измерения от среднего арифметического значения измеряемой величины. Следовательно, параметр σ характеризует качество измерений на данной установке, либо по данной методике.

Поскольку в конкретном эксперименте число измерений N ограни­чено, то вместо дисперсии σ² обычно рассматривают так называемую выборочную ди с персию S², которая является оценкой для σ. Очевидно, что . Поэтому далее будем рассматривать выборочную дисперсию S² и оцен­ку среднеквадратичного отклонения S.

Проведем М серий измерений некоторой величины X, аналогич­ных серии (3), и по формуле определим средние арифметические зна­чения измеряемой величины для каждой серии:

(11)

Очевидно, что в общем случае числа в серии (11) отличаются друг от друга и для этой последовательности можно было бы также построить гистограмму, которая при перейдёт в непрерывную кривую плотности распределения вероятности средних значений измеряемой вели­чины с параметрами и :

(12)

Оказывается, что среднеквадратичные отклонения результатов в сериях (3), (11) связаны между собой:

(13)

Отсюда видно, что дисперсия средних значений измеряемой величины может быть сделана существенно меньшей, чем дисперсия результатов измерений. С учётом (13) по результатам измерений можно определить оценки среднеквадратичных отклонений результатов измерений:

(14)

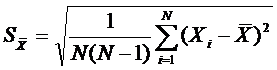(15)

Как уже указывалось ранее, в результате проведённых измерений необходимо определить интервал значений измеряемой величины (до­верительный интервал), внутри которого находится её истинное зна­чение. Предположим, что доверительный интервал известен и находит­ся в пределах . Тогда, используя функцию плотности распределения вероятности результатов измерения (10),можно определить вероятность Р того, что истинное значение измеряемой величины находится в указанном интервале:

(16)

Величина Р называется доверительной вероятностью. Чем меньше доверительный интервал, тем меньше соответствующая площадь под кривой p(X). Следовательно, вероятность того, что истинное значение величины X лежит в узком доверительном интервале, мала (P<<1) и, наоборот, с большой вероятностью (P≤1) мы можем гарантиро­вать нахождение истинного значения в широком доверительном интервале. Но, очевидно, что в этом случае уменьшается ценность среднего арифметического, как оценки истинного значения измеряемой величины. С использованием доверительной вероятности Р окончательный результат измерения физической величины в случае, когда отклонения её обусловлены случайной погрешностью, записывается в виде:

, (17)

где t_P,N – коэффициент Стьюдента, определяемый по задаваемой доверительной вероятности Р и числу измерений N. Коэффициент Стьюдента учитывает отклонение реальной кривой плотности распределения результатов измерения от гауссовой кривой (10) при малом числе измерений, что, как правило, реализуется на практике. Значение доверительной вероятности Р, определяющей окончательный результат, выбирают, исходя из требований, предъявляемых к измерениям. Обычно выбирают 0,68≤Р≤0,95. Если выбрано Р=0,68, то случайная погрешность в этом случае равна среднеквадратичному отклонению и окончательный результат записывается в виде:

(18)

Случайная погрешность определяет абсолютное откло­нение результатов измерения от истинного значения, поэтому она называется абсолютной случайной погрешностью. Отношение абсолютной случайной погрешности к среднему арифметическому значению измеря­емой величины называется относительной случайной погрешностью.

3.2. Полная погрешность прямых измерений

При проведении прямых измерений необходимо и, как правило, достаточно учитывать следующие погрешности: случайную 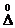, приборную 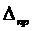и погрешность округления . Тогда результирующая абсолютная погрешность прямых измерений может быть определена по формуле:

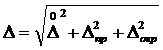(19)

Порядок вычисления полной абсолютной погрешности следующий: вначале вычисляются по отдельности - случайная 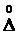, приборная погрешности и погрешность округления .

3.3. Случайная погрешность. Обычно признаком присутствия в изме­рениях случайной погрешности является случайное отклонение изме­ряемой величины от измерения к измерению. В этом случае, проведя порядка десяти измерений, проводят следующие вычисления:

I. По формуле (4) определяют среднее арифметическое значение измеряемой величины .

2. Определяют абсолютные погрешности отдельных измерений по
формуле (5) .

Если сумма этих погрешностей в серии измерений существенно отличается от нуля, необходимо увеличить число измерений.

3. Вычисляют среднеквадратичное отклонение по формуле (15) .

4. Задаваясь доверительной вероятностью Р при данном числе измерений по таблице 1(см.приложение), определяют значение коэффициента Стьюдента t_P,N. Тогда случайную абсолютную погрешность прямых измерений определяют по формуле: .

3.4. Приборная погрешность. Приборную погрешность вычисляют по классу точности К используемого прибора:

,

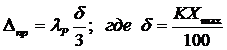где δ – предельная абсолютная погрешность прибора, вычисляется из формулы (2).

λ_P – коэффициент, определяемый надёжностью из­мерения. Значения этого коэффициента: .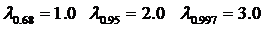

3.5. Погрешность округления. Чтобы понять причины возникновения погрешности округления, рассмотрим пример. Предположим, что мы измеряем длину некоторого предмета штангенциркулем с ценой деления нониуса 0,01 мм. Известно, что длина предмета равна, например, 16,015 мм. Какой отсчёт мы получим по шкалам штангенциркуля? Очевидно, получим 16,01, либо 16,02. И тот и другой отсчеты прави­льные, так как штангенциркуль, имея цену деления нониуса 0,01 мм округляет результат измерения до 0,01 мм. Ясно, что погрешность такого округления не может превосходить половины цены деления измерителя.

Аналогичные погрешности округления возникают при пользовании линейкой, микрометром, при отсчётах по шкалам стрелочных приборов, при пользовании цифровыми приборами и т.д.

Абсолютная погрешность округления определяется по формуле:

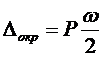
где ω - интервал округления, который равен цене деления изме­рительного прибора, если отсчёт берется с точностью до деления, половине цены деления, если отсчёты округляются до половины цены деления и т.д.

Окончательно формула для определения полной абсолютной погреш­ности принимает вид:

(20)

В силу разновеликости вкладов различных погрешностей в (20), как правило, нет смысла учитывать их все одновременно.

В процессе измерений могут возникнуть следующие ситуации:

1. Приборная погрешность 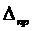существенно превосходит случайную погрешность 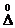. (Достаточно при этом, чтобы они отличались в несколько раз). В этом случае случайной погрешностью можно пренебречь.

2. Приборная погрешность существенно меньше случайной погрешности, тогда ею можно пренебречь.

3. Случайная и приборная погрешности близки друг другу. В
этом случае их необходимо учитывать одновременно.

У измерительных приборов, имеющих класс точности, погрешность округления обычно существенно меньше приборной погрешности и ею можно пренебречь. В то же время для ряда приборов (например, линейки, микрометры, штангенциркули т.д.) понятие приборной погрешности не имеет смысла и в этом случае при вычислении полной абсолютной погрешности предварительно сопоставляют погрешности случайную и округления.

Полная относительная погрешность прямых измерений определяется по формуле:

, (21)

где Δ – полная абсолютная погрешность,

– среднее ариф­метическое значение измеряемой величины.

Окончательный результат прямых измерений некоторой величины записывается в виде:

, (22)

где – нижняя и верхняя границы доверительного интер­вала.

Примечание: Вычисления случайной, приборной погрешностей и погреш­ности округления должны проводиться при одинаковой доверительной вероятности.

Прямые измерения могут быть однократными и многократными. Выбор той или иной методики измерений определяется следующими сооб­ражениями: если измеряемая величина изменяется со временем доста­точно быстро или характер её изменения неизвестен исследователю, то делают однократные измерения. Если же измеряемая величина достаточно долго остается неизменной, то делают многократные измерения. При этом могут возникнуть следующие ситуации:

1. Приборная погрешность является определяющей (то-есть су­щественно превосходит случайную погрешность). В этом случае дос­таточно провести однократное измерение. Однако, во избежание про­махов, обычно делают два-три измерения.

2. Если определяющей является случайная погрешность, то делают столько измерений, чтобы средняя абсолютная погрешность (6) была невелика. Обычно достаточно сделать 5-10 измерений.

3.6.Погрешность косвенных измерений

Пусть в некотором эксперименте определяются физическая вели­чина U, являющаяся функцией нескольких аргументов X, Y, Z, t, величины которых определяются в прямых измерениях (например, в качестве U может быть плотность тела, тогда X, Y, Z, t соответственно, его линейные размеры и масса). Другими словами, задана функциональная связь:

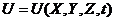(23)

На основании прямых измерений величин X, Y, Z, t оп­ределяют их средние значения и полные абсолютные погрешности. Подставляя средние значения аргументов в (23), получим:

(24) Поскольку эта величина также является случайной, возникает вопрос об отыскании того доверительного интервала, внутри которого нахо­дится её истинное значение. Полуширина этого интервала может быть определена по формулам:

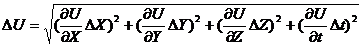, (25)

либо

, (26)

где ΔX, ΔY, ΔZ, Δ 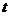– полные абсолютные погрешности прямых измерений величин X, Y, Z, t. Относительная погрешность косвенных измерений определяется по формуле:

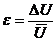(27)

3.7. Определение необходимого количества измерений

Увеличивая количество измерений N даже при неизменной их точности, можно увеличить надёжность измерений либо сузить дове­рительный интервал. Необходимое количество измерений для достижения требуемой точности при надёжности P можно определить, если предварительно сделать оценку среднеквадратичной погрешности измерения (по предварительным измерениям) и найти величину:

, (28)

где - требуемая погрешность измерения среднеквадратического, S - среднеквадратичное отклонение результатов измерений, определяется по формуле (14). Далее по таблице 2 Приложения оп­ределяют необходимое количество измерений.

3.8. Исключение промахов

Существует несколько приёмов для проведения анализа и отсева грубых погрешностей измерений. Рассмотрим один из них.

Если имеется некоторая выборка из генеральной совокупности с N ≤25, то можно воспользоваться методом вычисления максимального относительного отклонения:

,

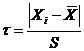где – наибольшее или наименьшее (подозреваемое как промах) значение измеряемой величины;

– среднее арифметическое значение измеряемой величина и её среднеквадратичное отклонение, вычисленные по выборке с учётом промахов по формулам (4) и (14).

По таблице 3 Приложения по заданной доверительной вероятнос­ти Р находят предельное значение относительного отклонения . Если ≤ , то данное измерение не отбрасывают, если же неравенство не соблюдается, то измерение отбрасывают как промах. После исключения промахов все характеристики () должны быть пересчитаны заново.

Не нашли, что искали? Воспользуйтесь поиском: