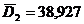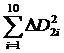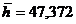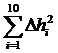ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
МЕТОДЫ СТАТИСТИЧЕСКОЙ ОЦЕНКИ ПАРАМЕТРОВ ЛИНЕЙНОЙ ЗАВИСИМОСТИ
4.I. Метод наименьших квадратов
На опыте часто приходится измерять пары величин X и Y, когда одна из них является функцией другой. Проведя измерения, пытаются, как правило, найти аналитический вид такой кривой, которая проходила бы как можно ближе к экспериментальным точкам. Например, если величины X и Y связаны линейной зависимостью:
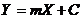 , (29)
, (29)
то задача исследований состоит в том, чтобы найти такие параметры m и C, при которых прямая наилучшим образом проходила бы через экспериментальные точки.
Линейная зависимость существенно упрощает анализ метода наименьших квадратов. Однако, даже в случае, когда зависимость между измеряемыми величинами нелинейная, можно попытаться представить её в таких координатах, чтобы получалась линейная связь. Например, связь между сопротивлением полупроводника и температурой нелинейна:
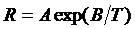 , (30)
, (30)
где А, В - постоянные.
Если провести замену 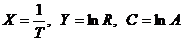 , то (30) примет вид:
, то (30) примет вид: 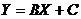 , то есть, получилось уравнение прямой. Поэтому, не нарушая общности, рассмотрим случай, когда величины X и Y связаны зависимостью (29). Пусть в некоторых измерениях мы получим N пар значений измеряемых величин:
, то есть, получилось уравнение прямой. Поэтому, не нарушая общности, рассмотрим случай, когда величины X и Y связаны зависимостью (29). Пусть в некоторых измерениях мы получим N пар значений измеряемых величин:
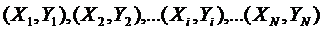 (31)
(31)
Предположим, что погрешность измерения величины X существенно меньше погрешности измерения Y, причём погрешностью ΔX можно пренебречь. (Такая ситуация часто реализуется в измерениях). Можно не принимать этого ограничения, но тогда анализ существенно усложняется.
Отклонение результата i - го измерения от прямой можно представить так:
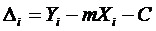 (32)
(32)
Сущность метода наименьших квадратов заключается в том, что оптимальное значение параметров m и C выбирается из условий минимальности суммы квадратов отклонения (32):
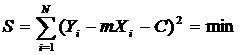 (33)
(33)
Рассматривая S как функцию переменных m и C, запишем условие её минимума:
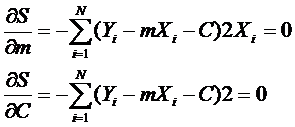 (34)
(34)
Тогда искомые параметры линейной зависимости m, C могут быть найдены из системы уравнений:
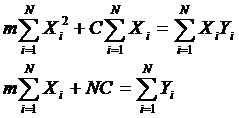 (35)
(35)
Решая систему (35), найдём
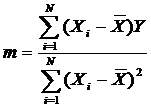 (36)
(36)
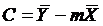 , где (37)
, где (37)
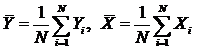 .
.
Среднеквадратичные отклонения величин m и C могут быть определены по формулам:
 (38)
(38)
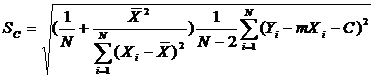 (39)
(39)
В том случае, когда известно, что исследуемая теоретическая кривая должна проходить через начало координат (т.е. С =0), параметр m и его дисперсия могут быть найдены по формулам:
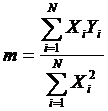 (40)
(40)
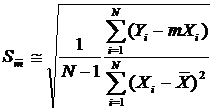 (41)
(41)
4.2. Метод парных точек
В том случае, когда требуется определить лишь угол наклона прямой [по угловому коэффициенту m в (29)], нет смысла проводить громоздкие вычисления по методу наименьших квадратов.
Пусть в результате измерений некоторых величин X, Y получено N точек. Возьмем пару точек 1 и (N/2)+1. Через них проходит прямая с угловым коэффициентом m1. Следующей паре точек 2 и (N/2)+2 отвечает коэффициент m2 и т.д. В результате получим N/2 значений параметра m, которые можно обработать обычным способом: найти среднее значение  и его среднеквадратичное отклонение
и его среднеквадратичное отклонение  . Окончательный результат запишется в виде
. Окончательный результат запишется в виде  , Δ от
, Δ от  до
до 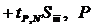 . Следует отметить, что при нахождении параметра m нет необходимости строить экспериментальный график.
. Следует отметить, что при нахождении параметра m нет необходимости строить экспериментальный график.
4.3. Округление окончательного результата измерений
Точность обработки числового материала должна быть согласована с точностью самих измерений. Вычисления, проведённые с большим числом десятичных знаков, чем это необходимо, необоснованно затрудняют вычисления. В то же время недостаточная точность вычислений ухудшает результаты измерений. Поэтому в вычислениях следует руководствоваться следующим правилом: погрешность, получающаяся в результате вычислений, должна быть по крайней мере на порядок меньше результирующей погрешности измерений.
Необходимо руководствоваться следующими правилами действия над приближёнными числами:
I. При сложении и вычитании в результате следует сохранить столько десятичных знаков, сколько их в приближённом числе с наименьшим числом десятичных знаков.
2. При умножении двух приближённых чисел, имеющих одинаковое число значащих цифр, окончательный результат должен содержать такое же количество значащих цифр. Если число значащих цифр в сомножителях различно, то результат должен иметь столько же значащих цифр, что и наименее точный сомножитель.
3. При возведении в степень (в том числе и в дробную) результат должен иметь столько же значащих цифр, что и основание.
С другой стороны, среднеквадратичная погрешность измерений при сравнительно небольшом числе измерений (N~ 10) определяется с погрешностью более 30%, поэтому в результирующей погрешности следует оставлять одну значащую цифру, если она больше трёх, и две значащие цифры, если первая из них меньше четырёх. Например, если Δ = 0,635, то следует округлить Δ = 0,6, если же Δ = 0,218, то нужно оставить Δ =0,22.
В среднем значении окончательного результата измерений последняя значащая цифра оставляется в том же десятичном разряде, что и последняя значащая цифра в погрешности.
Ниже приведём примеры правильного и неправильного округления окончательного результата:
| Правильно: 1. (39,4 ± 0,6) В 2. (121,4 ± 2,4) с 3. (2,62± 0,05)·10-19 Кл 4. (19,02± 0,26) г |
Неправильно:
1. (39,421±0,625) В
2. (121,37 ±2,39) с
3. (2,619·10-19±5,36·10-21) Кл
4. (19,025±0,26) г
Во избежание накопления ошибок, связанных с округлением при вычислениях, рекомендуется в промежуточных расчётах сохранять число знаков на один - два больше, чем это рекомендуется вышеуказанными правилами.
Примечание: Значащими цифрами числа называются все цифры от 1 до 9, а также нуль, если он стоит в середине или в конце числа. Например: число 0,39 имеет две значащих цифры, а числа 10,9 и 10,90 соответственно три и четыре значащих цифры.
4.4. Основные требования к графику
1. Наименьшее расстояние, считываемое с графика, должно быть не
меньше абсолютной погрешности измерений.
2. Масштаб выбирается таковым, чтобы кривые заполняли все поле
чертежа, а физическая сущность исследуемого явления должна быть раскрыта максимально ясно. Выбор начального и конечного значения шкал
на осях проводится, исходя из полного использования поля графика.
3. Обычно на оси абсцисс откладывают аргумент, а на оси ординат –функцию. Масштаб графика должен быть простым. Лучше всего, если 1 см
соответствует единице измеряемой величины, либо её значению, кратному 10 (1; 10; 100; 0,1; 0,01;...............................................................). Менее удобен, но возможен масштаб, кратный 2 или 5 (2, 4, 5, 0,5....).
4. На осях графика указывается символ, либо название измеряемой
величины и указывается единица измерения её. Если измеряемые величины на много порядков больше или меньше единицы, то удобно представлять
их в форме с общим множителем, стоящим у символа.
5. Экспериментальные точки наносятся чётко без вспомогательных
построений.
6. Точки не соединяются ломаной прямой, а проводится сглаживающая кривая.
7. При сравнении теоретической кривой с данными эксперимента
экспериментальные точки на графике, как правило, не соединяются (при
этом точки теоретической кривой не должны быть видны на графике).
8. Строят графики мягкими графитовыми карандашами. Применение
цветных карандашей и ручек нежелательно.
9. Если на график наносится несколько кривых, то каждой кривой
присваивается номер, а на свободном поле графика эти номера расшифровываются.
СПИСОК ЛИТЕРАТУРЫ
5.1. Зайдель А.Н. Элементарные оценки ошибок измерений. Л., Наука, 1967,
88 с.
5.2. Сквайре Дж. Практическая физика (пер. с англ.). М., Мир, 1972, 246 с.
5.3. Худсон Д. Статистика для физиков (пер. с англ.), М., Мир, 1979, 296 с.
5.4. Румшинский Л.З. Математическая обработка результатов эксперимента. М., Наука, 1971, 192 с.
5.5. ГОСТ 8.011-72 Показатели точности измерений и формы представления результатов измерения.
5.6. ГОСТ 16263-70. Метрология. Термины и определения.
5.7. Львовский Е.Н. Статистические методы построения эмпирических формул. М., Высшая школа, 1982, 224 с.

ПРИЛОЖЕНИЕ 2
Необходимое число измерений N для получения заданной
случайной погрешности
Таблица 2
| P μN,P | 0.5 | 0.7 | 0.9 | 0.95 | 0.98 | 0.99 | 0.999 |
| 1.0 | |||||||
| 0.5 | |||||||
| 0.4 | |||||||
| 0.3 | |||||||
| 0.2 | |||||||
| 0.1 | |||||||
| 0.05 |
ПРИЛОЖЕНИЕ 3
Максимальное относительное отклонение τP
Таблица 3
| Кол.изм N | Доверительная | вероятность | р | |
| 0.90 | 0.95 | 0.975 | 0.99 | |
| 1,41 | 1,41 | 1,41 | 1,41 | |
| 1,65 | 1,69 | 1,71 | 1,72 | |
| 1,79 | 1,87 | 1,92 | 1,96 | |
| 4 б | 1,89 | 2,00 | 2,07 | 2,13 |
| 1.97 | 2,09 | 2,18 | 2,27 | |
| 2,04 | 2,17 | 2,27 | 2,37 | |
| 2,10 | 2,24 | 2,35 | 2,46 | |
| 2,15 | 2,29 | 2,41 | 2,54 | |
| 2,19 | 2,34 | 2,47 | 2,61 | |
| 2,23 | 2,39 | 2,52 | 2,66 | |
| 2,26 | 2,43 | 2,56 | 2,71 | |
| 2,30 | 2,46 | 2,60 | 2,76 | |
| 2,33 | 2,49 | 2,64 | 2,80 | |
| 2,35 | 2,52 | 2,67 | 2,84 | |
| 2,38 | 2,55 | 2,70 | 2,87 | |
| 2,40 | 2,58 | 2,73 | 2,90 | |
| 2,43 | 2,60 | 2,75 | 2,93 | |
| 2,45 | 2,62 | 2,78 | 2,96 | |
| 2,47 | 2,64 | 2,80 | 2,98 | |
| 2,49 | 2,66 | 2,82 | 3,01 | |
| 2,50 | 2,68 | 2,84 | 3,03 | |
| 2,52 | 2,70 | 2,86 | 3,05 | |
| 2,54 | 2,72 | 2,88 | 3,07 |
ПРИЛОЖЕНИЕ 4
Пример расчёта погрешностей измерений в лабораторном практикуме
Задача. Определить плотность вещества трубки и погрешность её измерения. Рабочая формула, по которой определяется плотность вещества трубки:
 , (1)
, (1)
где m – масса образца; D1, D2 – внешний и внутренний диаметры трубки соответственно; h – высота трубки.
Поскольку плотность в соответствии с (1) определяется по результатам измерения параметров m, D1, D2, h, то налицо косвенные измерения и, следовательно, необходимо определить погрешность косвенных измерений.
1. Выведем формулу для определения относительной погрешности измерения плотности. Известно, что относительная погрешность косвенных измерений некоторой величины U=U(X, Y, Z), выражается формулой:
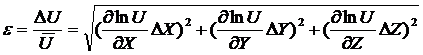 , (2)
, (2)
где ΔX, ΔY, ΔZ – абсолютные погрешности прямых измерений величин X, Y, Z.
Чтобы применить (2) к условиям нашей задачи, необходимо:
а) Прологарифмировать алгебраическое выражение (1), но при этом иметь в виду, что логарифм именованного(имеющего размерность) числа не имеет смысла:
 (3)
(3)
б) Продифференцировать (3) по тем параметрам, которые вносят вклад в результирующую погрешность измерений (для нашей задачи это m, D1, D2, h).
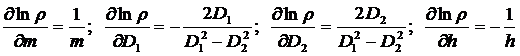 (4)
(4)
в) Подставив (4) в (2), получим формулу для определения относительной погрешности измерения плотности:
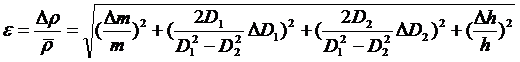 , (5)
, (5)
где Δm, ΔD1, ΔD2, Δh – абсолютные погрешности измерений величин m, D1, D2, h.
Если эти величины определяются в прямых измерениях, то их полные абсолютные погрешности выражаются в общем случае:
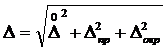 , (6)
, (6)
где 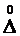 – случайная погрешность;
– случайная погрешность; 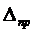 – приборная погрешность;
– приборная погрешность;  – погрешность округления.
– погрешность округления.
Следовательно, для определения погрешности измерения плотности необходимо определить абсолютные погрешности Δm, ΔD1, ΔD2, Δh и средние значения m, D1, D2, h. (В формуле (5) так обозначены средние значения этих величин).
Измерения. Проведём при помощи штангенциркуля измерения D1, D2, h. (В соответствии с методическими указаниями рекомендуется эти измерения проделать по 10 раз).
Результаты измерений D1, D2, h представлены в виде таблицы 3.
Во избежание промаха взвесим образец трижды и допустим, что:
m1 = 0.13755 кг, m2 = 0.13734 кг, m3 = 0.13756 кг.
Расчёт.
а) Определим среднюю массу образца:
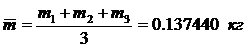 (7)
(7)
В отсутствие случайной погрешности (или при малом числе измерений) погрешность взвешивания определяется погрешностью округления, приблизительно равной половине цены деления весов. Однако в данной работе рекомендуется принять погрешность взвешивания равной половине массы наименьшего разновеса, используемого при взвешивании. Эта оценка заведомо больше погрешности округления. Следовательно: 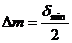 , где
, где 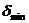 – масса наименьшего разновеса.
– масса наименьшего разновеса.
Пусть 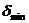 = 0.1·10-4 кг, следовательно:
= 0.1·10-4 кг, следовательно:
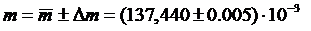 кг (8)
кг (8)
б) Определим средние значения остальных величин 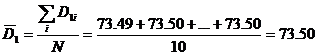 мм, (9)
мм, (9)
где N – число измерений.
Аналогично:
 = 38.93 мм (10)
= 38.93 мм (10)
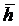 = 47.37 мм (11)
= 47.37 мм (11)
в) Определим абсолютные погрешности i -х измерений, их квадраты, занесём результаты в таблицу 3. Сложим квадраты указанных погрешностей.
Абсолютная погрешность i-го измерения определяется по формуле:  .
.
Поскольку суммы абсолютных погрешностей измерений каждой из величин невелики, это значит, что число измерений N =10 достаточно для статистической обработки результатов измерений.
г) Определим случайную погрешность 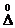 , которая входит в формулу (6). Для этого вначале найдём среднеквадратичную погрешность по формуле:
, которая входит в формулу (6). Для этого вначале найдём среднеквадратичную погрешность по формуле:
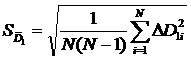 (12)
(12)
Подставляя в (12) значения из таблицы 3, находим  = 2.1·10-3 мм,
= 2.1·10-3 мм,  = 5.7·10-3 мм,
= 5.7·10-3 мм,  = 0.17 мм.
= 0.17 мм.
Так как число измерений мало (N = 10), то для определения случайной погрешности необходимо ввести коэффициент Стьюдента, округлённый по задаваемой доверительной вероятности Р и числу измерений N (таблица 2):
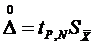
Зададимся доверительной вероятностью Р = 0.95 и по табл.1 (при N = 10) находим 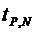 = 2.3.
= 2.3.
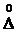 D1 = 4.83·10-3 мм (13)
D1 = 4.83·10-3 мм (13)
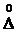 D2 = 13.11·10-3 мм (14)
D2 = 13.11·10-3 мм (14)
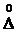 h = 0.391 мм (15)
h = 0.391 мм (15)
д) Приборная погрешность 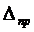 , входящая в формулу (6), обычно определяется по классу прибора:
, входящая в формулу (6), обычно определяется по классу прибора: 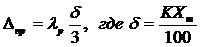 , где К – класс прибора (в процентах), Xm – предел измерения прибора, δ – максимальная абсолютная погрешность прибора, λр – нормирующий множитель, определяемый по доверительной вероятности (при Р = 0.95 λр = 2.0).
, где К – класс прибора (в процентах), Xm – предел измерения прибора, δ – максимальная абсолютная погрешность прибора, λр – нормирующий множитель, определяемый по доверительной вероятности (при Р = 0.95 λр = 2.0).
Поскольку штангенциркули не имеют класса, то следует положить
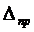 =0 (16)
=0 (16)
е) Погрешность округления  может быть определена по формуле:
может быть определена по формуле:  , где ω – интервал округления (обычно равен цене деления, либо половине её в зависимости от того, с какой точностью мы делаем отсчёт).
, где ω – интервал округления (обычно равен цене деления, либо половине её в зависимости от того, с какой точностью мы делаем отсчёт).
Для штангенциркуля интервал округления равен цене деления нониуса. Для нашего штангенциркуля интервал округления ω = 0.01 мм и одинаков для всех измерений. Так как доверительная вероятность выбрана равной 0.95, то
 мм (17)
мм (17)
ж) Подставляя значения из формул (13, 14, 15, 16, 17) в формулу (6), получим полные абсолютные погрешности прямых измерений:
ΔD1 = 6.95·10-3 мм, ΔD2 =1.6·10-2 мм, Δh = 0.4 мм (18)
Из анализа величин абсолютных погрешностей (13, 14, 15) и погрешности округления (17) видно, что можно было при расчёте ΔD1 пренебречь величиной 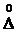 D1, а при расчёте Δh – величиной
D1, а при расчёте Δh – величиной 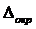 h.
h.
Получим:
m = (137.440±0.005)·10-3 кг
D1 = (73. 497±0.007) мм
D2 = (38.90±0.016) мм (19)
h = (47.4±0.390) мм
з) Подставляя величины (19) в формулу (5), получим относительную погрешность измерения плотности:
ε = 0.0029
и) Подставляя в формулу (1) средние значения измеренных величин, получим среднее значение плотности:
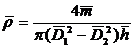 = 0.9507·103 кг/м3
= 0.9507·103 кг/м3
Зная 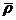 и ε, можно найти абсолютную погрешность измерения плотности:
и ε, можно найти абсолютную погрешность измерения плотности: 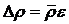 = 2.76 кг/м3.
= 2.76 кг/м3.
Окончательно:
Плотность вещества трубки – 950.7 кг/м3, Δ от (-2.8 до +2.8) кг/м3, Р = 0.95.
|
Не нашли, что искали? Воспользуйтесь поиском:
 , мм2
·10-6
, мм2
·10-6
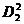 , мм 2
·10-6
, мм 2
·10-6