Сила давления жидкости на плоскую поверхность

Сила давления на плоскую поверхность определяется по формуле:

, (1.9)

где h_с - глубина погружения центра тяжести площади фигуры; w - площадь фигуры (смоченной поверхности).

При определении силы давления строят эпюру гидростатического давления. Для построения эпюры в точке пересечения свободной поверхности воды со стенкой откладывают величину избыточного гидростатического давления, в этой точке оно равно 0. Величина избыточного давления на максимальной глубине откладывается перпендикулярно поверхности, эта величина определяется по формуле g·h (h -глубина слоя воды перед стенкой).

Величину силы давления можно определить произведением площади эпюры на ширину стенки. (Величина силы давления численно равна объему тела давления). Площадь треугольника определяется как произведение половины основания на высоту; основание равно (g·h), высота – h, тогда сила давления Р = (g·h)∙h∙b/2, где b - ширина стенки.

Рис. 1.3. Эпюры гидростатического давления на вертикальную и наклонную стенки

Равнодействующая силы давления приложена в центре давления. Для треугольной эпюры центр давления располагается на расстоянии, равном ⅔ от вершины эпюры (точки пересечения поверхности воды со стенкой) - на схеме h_д = h`. В общем случае центр давления определяют по формуле

, (1.10)

где – глубина расположения центра тяжести смоченной поверхности;

- момент инерции смоченной поверхности относительно горизонтальной оси, проходящей через центр тяжести смоченной поверхности;

- площадь смоченной поверхности.

Для прямоугольника с шириной b и высотой h момент инерции равен , для круга – .

Задача 1.5. Определить давление воды на стенку при ее ширине b = 3 м и глубине слоя воды перед стенкой h = 4 м.

Решение: Сила давления определяется по формуле (1.9): g - удельный вес воды, g = 1 Т/м³, h_с - центр тяжести смоченной поверхности стенки находится на глубине 2м, w -площадь стенки; w = 3∙4=12 м². Тогда сила давления P = 1∙2∙12 = 24Т. Центр давления будет находиться на глубине 2/3 от глубины воды перед стенкой или (2/3)∙4 = 2,67м; или, используя формулу (1.10)

y _Д= 2 + (3∙4³)/(12∙2∙12) = 2,67 м.

Закон Архимеда

На тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной телом жидкости. При плавании тела сила тяжести G равна выталкивающей силе 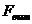, т.е. G = 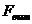. Выталкивающая сила равна

(1.11)

или (1.12)

где - объем вытесняемой телом жидкости;

- плотность жидкости;

- ускорение свободного падения;

-удельный вес воды в Н/м³, Г/см³, кГ/л или Т/м³.

Объем вытесняемой телом воды определяется как площадь погруженного в воду тела на глубину погружения тела под уровень воды (осадка). Тогда закон Архимеда можно представить в виде:

(1.13)

Задача 1.6. Определить максимальную грузоподъемность понтона размером 3х4м и осадке h = 0.5 м.

Решение

= = 6 т [м∙^∙м∙ м∙Т/м³ = Т]

Удельный вес можно выразить в Т/м³, = 1 Т/м³. Грузоподъемность понтона (водоизмещение) в данном случае общая с учетом веса самого понтона. При плавании тела весом в 1 Т, будет вытесняться 1 м³ воды (1 кГ → 1 л, 1 Г → 1 см³.).

Задача 1.7. В воде плавает понтон d = 1м, вес самого понтона 20кГ, вес груза, который находится на понтоне, составляет 60 кГ. Определить осадку понтона h.

Решение

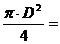
Общий вес понтона и груза G = 20+60 = 80 кГ=0,08 Т. Площадь понтона определяется по формуле = 0,785 м².

G = ,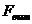

0,8=0,785∙h∙g → h=0,08/(0,785 ∙ 1)=0,12(м)

Гидродинамика

Не нашли, что искали? Воспользуйтесь поиском: