Движение жидкости в каналах

Скорость движения воды в канале определяется по формуле Шези

(2.20)

где С- коэффициент Шези, определяемый по формуле Павловского,

(2.21)

где - гидравлический радиус, м;

– коэффициент, вычисляемый по формуле в зависимости от величины гидравлического радиуса; при R<1м , при R>1м ;

- коэффициент шероховатости, определяется по справочным данным и изменяется в пределах от 0,011 до 0,014 и более.

Коэффициент Шези С можно определить по формуле

(2.22)

Задача 2.10. Выполнить гидравлический расчет прямоугольного канала при расходе Q = 100 л/с. Коэффициент шероховатости принять n = 0,014, скорость воды в канале V=1 м/с.

Рис. 2.6. Разрез прямоугольного канала

Решение.

Площадь живого сечения канала определится из выражения (2.2)

= = 0,1(м² )

Наполнение в канале принимается в пределах 0.5÷0.8, в данном случае можно принять h/a=0,5 (где а – ширина канала). Высота воды в канале = . Площадь сечения канала будет равна

Отсюда = 0,447 (м) Ширину канала можно округлить до десятых долей, т.е. принять 0,4м. Тогда глубина воды в канале равна = = = 0,25 м.

Гидравлический радиус для канала равен R = = = = 0.11 м. Коэффициент Шези C определится по формуле (2.21), предварительно высчитывается коэффициент = = 0.177.

= = 48,33.

Из формулы (2.20) гидравлический уклон равен

= = 0,00344

Задача 2.11. Определить расход воды в канале прямоугольного сечения (рис.2.7) при ширине канала а = 0,6м, наполнении h/ a =0,5, гидравлическом уклоне 0,004, коэффициенте шероховатости n =0,014.

Решение.

Глубина слоя воды h = = 0,3 м. Площадь живого сечения ω = = 0,18 м². Гидравлический радиус R = = = 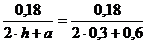0,15

= = 0.177

= = 51,06.

Расход воды в канале определится по формуле (2.2), для чего первоначально вычисляется скорость движения воды в канале по формуле (2.20)

= = 1,25 (м/с)

= = 0,225 (м³/с) = 225 (л/с)

Задача 2.12. В канале трапецеидального сечения (ширина канала понизу b₁ =0,8 м, глубина воды h =0,5м) коэффициент заложения откосов m =1 (m= ctg α =a/h), расход воды в канале Q = 1м³/с. Коэффициент шероховатости равен n = 0,014. Определить гидравлический уклон канала при равномерном движении воды.

Рис. 2.7. Разрез трапецеидального канала

Решение.

При ширине канала поверху и а=h площадь поперечного сечения канала равна:

ω = = 0,65(м²)

Смоченный периметр будет равен 2,21 (м)

Гидравлический радиус равен R = = = 0,29

Скорость течения воды = 1.54 м/с.

= = 0.177

= = 57,37

Из формулы (2.20) гидравлический уклон равен

= = 0,0025

Приложения

Приложение 1.

Не нашли, что искали? Воспользуйтесь поиском: