
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Принцип неопределенности Гейзенберга. Главная особенность поведения микрочастиц состоит в том, что динамические параметры, как координата
Главная особенность поведения микрочастиц состоит в том, что динамические параметры, как координата, импульс, энергия, момент импульса и другие, используемые для описания поведения материальной точки (макрочастицы) не могут быть точно одновременно измерены. Так, например, электрон или протон не могут иметь одновременно однозначных значений координаты «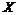 » и проекции импульса «
» и проекции импульса « ». Неопределенности, обусловленные законами микромира, для названных параметров, как показала квантовая механика, должны удовлетворять соотношению:
». Неопределенности, обусловленные законами микромира, для названных параметров, как показала квантовая механика, должны удовлетворять соотношению:
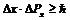 . (5 – 2)
. (5 – 2)
Из (5 – 2) следует, что чем меньше неопределенность одной величины, тем больше неопределенность другой канонически сопряженной ей величины.
Аналогично (5 – 2) запишется произведение неопределенностей для другой пары канонически сопряженных величин (энергии и времени):
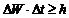 . (5 – 3 )
. (5 – 3 )
Принцип неопределённости Гейзенберга гласит: «произведение неопределенностей значений двух сопряженных параметров не может быть меньше постоянной Планка 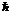 ».
».
Соотношение неопределенности указывает, в какой мере можно пользоваться понятиями классической механики применительно к микромиру, и является фундаментальным положением квантовой механики.
3. Уравнение Шредингера. Смысл 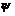 - функции
- функции
В 1926 г. Э. Шредингер, исходя из оптико–механической аналогии, записал основное уравнение нерелятивистской квантовой механики для пси – функции, которое для стационарных состояний микрочастиц принимает выражение:
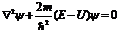 , (5 – 4)
, (5 – 4)
где 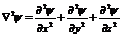 - оператор Лапласа для
- оператор Лапласа для 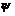 - функции,
- функции, 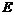 -полная энергия микрочастицы,
-полная энергия микрочастицы, 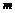 – масса частицы,
– масса частицы, 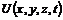 – потенциал силового поля, взятый с обратным знаком.
– потенциал силового поля, взятый с обратным знаком.
Пси–функция зависит от координат и времени, описывает состояние системы, позволяет находить среднее значение характеризующих систему физических величин и квадрат ее модуля определяет вероятность обнаружения микрочастиц в объеме:
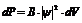 , (5 – 5)
, (5 – 5)
где  – коэффициент пропорциональности.
– коэффициент пропорциональности.
Следовательно, квантовая механика дает не динамический ответ (однозначный), а статистический (вероятностный). Уравнение Шредингера дает выражение 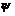 - функции. Сама
- функции. Сама 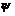 - функция должна быть однозначной, непрерывной и конечной (стандартные условия
- функция должна быть однозначной, непрерывной и конечной (стандартные условия 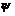 - функции).
- функции).
Применим уравнение Шредингера для описания состояния микрочастицы, находящейся в бесконечно глубокой одномерной потенциальной яме (рис.32).
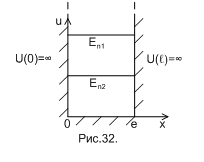
Пусть потенциальная энергия внутри ямы равна нулю (отсутствие гравитации) при  и бесконечно большая вне ямы (
и бесконечно большая вне ямы ( и
и 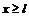 ). Так как «яма» одномерна, то оператор Лапласа для
). Так как «яма» одномерна, то оператор Лапласа для 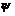 - функции запишется:
- функции запишется:
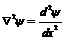 . (5 – 6)
. (5 – 6)
Из-за высоких потенциальных стенок ямы микрочастица за пределами ямы находиться не может, следовательно, 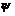 - функция равна нулю при
- функция равна нулю при 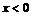 и
и 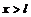 , а так же (по условию ее непрерывности) при
, а так же (по условию ее непрерывности) при 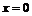 и
и 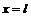 , т.е.
, т.е.
 . (5 – 7)
. (5 – 7)
Внутри ямы, где 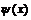 не равна нулю, уравнение Шредингера запишется:
не равна нулю, уравнение Шредингера запишется:
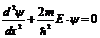 . (5 – 8)
. (5 – 8)
Дифференциальное уравнение (5 – 8) приведем к стандартному виду, если обозначить
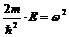 (5 – 9)
(5 – 9)
Решением дифференциального уравнения (5 – 3) будет гармонический закон, т.е. волновая 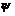 - функция будет изменяться по синусоидальному закону:
- функция будет изменяться по синусоидальному закону:
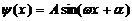 (5 – 10).
(5 – 10).
Из условия 
 , получаем
, получаем  ≡0. Из условия
≡0. Из условия 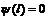 ;
; 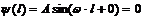 , получаем
, получаем
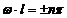 , (5 – 11)
, (5 – 11)
где  =1; 2; 3; ….
=1; 2; 3; ….
Выразив из (5 – 11) 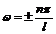 и подставив в (5 – 9), получим квантовое распределение энергии по уровням:
и подставив в (5 – 9), получим квантовое распределение энергии по уровням:
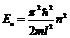 (5 – 12).
(5 – 12).
Подставив 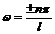 в (5 – 10), получим уравнение
в (5 – 10), получим уравнение  - функции для различных уровней энергии внутри ямы:
- функции для различных уровней энергии внутри ямы:
 . (5 - 13)
. (5 - 13)
Графики  показаны на (рис.33) для трех уровней.
показаны на (рис.33) для трех уровней.
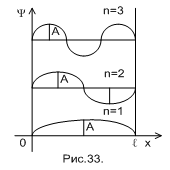
С учетом того, что вероятность нахождения частицы пропорциональна 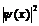 , приходим к следующим выводам:
, приходим к следующим выводам:
1) на уровне 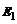 вероятнее всего обнаружить микрочастицу около центра ямы;
вероятнее всего обнаружить микрочастицу около центра ямы;
2) на уровне энергии 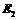 вероятнее всего обнаружить частицу вблизи координат
вероятнее всего обнаружить частицу вблизи координат  и
и 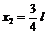 и т.д.
и т.д.
Полученные результаты свидетельствуют о том, что поведение микрочастиц в ограниченном объеме резко отличается от поведения классических молекул идеального газа. Например, в закрытом пространстве космического корабля в состоянии невесомости молекулы по классике распределяются равновероятно во всем объеме корабля.
Не нашли, что искали? Воспользуйтесь поиском: