Основные принципы временной дискретизации при моделировании процессов эволюции систем

На начальном этапе вычислительного эксперимента производится формирование полигона исходной топологической структуры объекта моделирования. В простейшем случае, а именно - полигона поверхностного типа, полигон моделирования представляется в виде совокупности атомов определенного типа (пример графического отображения структуры в начальный момент времени представлен на рис. 3.4).

По условию постановки задачи считается, что атомы типов А и В могут совершать в процессе эволюции системы во времени:

· диффузионные перемещения по поверхности подложки (по механизму термической активации), благодаря наличию свободных соседних ячеек подложки;

· химическое взаимодействие между собой, приводящее к образованию устойчивых молекулярных комплексов, обладающих существенно большими (чем для индивидуальных атомов типа А и В) значениями энергии активации поверхностной диффузии;

· уход (или приход) с подложки ввиду наличия адсорбционно-десорбционного равновесия между подложкой и окружающей газовой средой, содержащей в своем составе атомы типа А и В.

Таким образом, можно заключить, что, даже в первом приближении, при моделировании процесса эволюции системы возникает необходимость учета достаточно широкого спектра разнородных элементарных ФХП, обладающих различными характеристическими временами их реализации (прежде всего, в зависимости от значений энергий активации элементарных физико-химических процессов).

Процесс моделирования по методу клеточных автоматов производится во времени в режиме «шаг за шагом», через определенные, наперед заданные, интервалы времени – шаг временной дискретизации. Ввиду существенного различия характеристических времен элементарных ФХП возникает проблема выбора оптимальной временной дискретизации, закладываемой при моделировании. Основная трудность, возникающая при выборе оптимального значения временной дискретизации, состоит в том, что необходимо выполнить требование о правомерности его использования как для всех возможных типов заполнения атомами (молекулами) индивидуальных ячеек полигона моделирования, так и – всего рассматриваемого спектра элементарных ФХП.

Атомы (молекулы), находящиеся в конденсированных средах (в рассматриваемом случае - ячейках), обладают колебательным движением относительно центра равновесия с частотой порядка 10¹¹ - 10¹² (10⁹ - 10¹⁰) Гц. Каждое колебательное движение атома (молекулы) можно рассматривать в качестве «потенциальной попытки» реализовать тот или иной элементарный ФХП, которой ставится в соответствии определенная вероятность наступления этого события (в случае детерминированного клеточного автомата эта вероятность равна единице). В этой связи представляется уместным и естественным использовать в качестве шага временной дискретизации параметр: . Однако, такой подход на пути преодоления трудностей оптимизации шага временной дискретизации представляется крайне проблематичным по следующим причинам:

· расхождение параметра 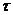для различных атомно-молекулярных объектов, расположенных в ячейках полигона моделирования, может быть весьма значительным: 10^-9 – 10^-12;

· использование столь малых значений шага временной дискретизации приведет к неоправданно большому суммарному количеству шагов моделирования;

· в принципе отвергается любая возможность реализации ускоренных режимов моделирования (например, чтобы за один шаг моделирования произошло изменение состояния определенного количества ячеек полигона).

Для согласования вышеперечисленных моментов необходимо разработать общие принципы вычисления вероятностей реализации ФХП за определенный промежуток времени, превосходящий длительность, определяемую параметром 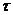для колебательного движения атомов (молекул). Для этого поступим следующим образом [6]. Обозначим посредством вероятность события, что элементарный процесс может быть реализован за время (, где 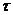- период тепловых колебаний атома). Вероятность наступления противоположного события (процесс не реализуется) должна удовлетворять очевидному условию нормировки:

.

(3.1)

Определим вид функции распределения для вероятности . Вероятность события, что процесс не реализуется за промежуток времени , может быть представлена в виде (здесь учтено то обстоятельство, что оба случая не реализации процесса за время и являются статистически независимыми событиями):

.

(3.2)

В первом приближении, ввиду малости промежутка времени , вероятность может быть выражена в виде линейной функции:

.

(3.3)

где - константа, характерная для рассматриваемого процесса.

На основании выражений (3.2) и (3.3) имеем:

.

(3.4)

Разлагая функцию в степенной ряд по переменной , и ограничиваясь линейным приближением, имеем:

.

(3.5)

Подставляя выражение (3.5) в выражение (3.4) получаем дифференциальное уравнение

(3.6)

Решением уравнения (3.6) является функция распределения вида:

(3.7)

Для определения значения постоянной А воспользуемся условием, что вероятность реализации процесса за нулевой отрезок времени равна нулю, а, следовательно, (согласно выражению (3.1)). Из этого следует, что постоянная А в выражении (3.7) равна единице, а выражение (3.7) имеет вид:

(3.8)

Для определения константы а, используемой в выражении (3.8), введем в рассмотрение для каждого элементарного ФХП понятия:

· «характеристическое время» элементарного процесса - ;

· «характеристическая вероятность» элементарного процесса - .

Взаимосвязь между параметрами и может быть установлена на основании аппарата статистической механики, в приближении, что элементарный ФХП является случайным процессом пуассоновского типа [7].

С учетом принятых понятий и выражения (3.8) имеем:

(3.9)

Константа а определяется из выражения (3.9) в виде:

(3.10)

Подставляя а из выражения (3.10) в выражение (3.8), для вероятности события типа - «не реализация процесса в течении интервала времени », имеем:

(3.11)

Подставляя (3.11) в выражение (3.1) для искомой вероятности реализации процесса за интервал времени имеем:

(3.12)

Функция распределения (3.12) позволяет определить вероятность реализации рассматриваемого элементарного ФХП по истечении любого интервала времени , в том числе, намного превосходящего период атомных (молекулярных) колебаний объектов, находящихся в ячейках полигона моделирования.

Не нашли, что искали? Воспользуйтесь поиском: