
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Решение дробно- рациональных
Неравенств с одной переменной методом интервалов
Дробно-рациональным называют неравенство вида  (1)
(1)
Вместо знака > могут стоять знаки <, ≥, ≤.), где и - многочлены.
План решения.
1. Если неравенство не имеет вид (1), то привести его к этому виду: перенести все слагаемые в левую часть, привести к общему знаменателю, а в правой части оставить нуль.
2. Найти нули числителя - корни уравнение P(x)=0.
3. Найти нули знаменателя – корни уравнения Q(х)=0.
4. Нанести нули числителя на числовую прямую с учетом знака неравенства:
- если неравенство нестрогое (стоят знаки ≥, ≤), то точки закрашенные (числитель может равняться нулю);
- если неравенство строгое (стоят знаки >,<), то точки не закрашенные.
5. Нанести нули знаменателя на числовую прямую: точки не закрашенные для любого знака неравенства (знаменатель не может равняться нулю).
6. Определить кратность нулей.
Пример. Нули числителя: х1=-5; х2= 2; х3= 7
Нули знаменателя: х4=х5=2; х6=7.
Корни: х = -5 кратности 1, х = 2 кратности 3, х = 7 кратности 2.
Замечание 1. Корни четной кратности подчеркнуть двойной чертой.
7. Найти знак левой части неравенства на каждом из полученных интервалов. Для этого на одном из интервалов выберем какое-то значение x=x0 и, подставив это значение в левую часть неравенства, определим знак А(х) на выбранном интервале (метод пробных точек), а потом учесть, что:
а) А(х) меняет знак при переходе от одного промежутка к соседнему через корень нечетной кратности;
б) А(х) не меняет знак при переходе через корень четной кратности.
8. Выберем те промежутки, где выполняется заданное неравенство (отметим их штрихами - заборчиком).
Замечание 2. В случае A(x)³0 корни уравнения A(x)=0 являются решениями неравенства (закрашенные точки на числовой прямой).
4. Запишем ответ.
Пример 1.

1. Нули числителя: (х –5)(2 х +6)=0 Û х =5 или х =−3;
2. Нули знаменателя: (6–3 х)(х +8)=0 Û х =2 или х =−8.
3.
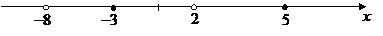 |
Нанесем полученные значения х на числовую прямую
4. Определим знак левой части неравенства на интервале [5; +¥).
х =6, 
Не нашли, что искали? Воспользуйтесь поиском: