
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задания (для тех, кто желает знать больше).
№1. Решите неравенство:
а) 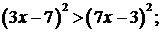
б) 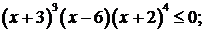
в) 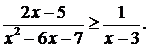
№2. Постройте эскизы графиков функций:
а)  ; б)
; б)  .
.
Метод интервалов. В. 1.
1. Решить неравенство:
а) (х - 3)(х + 2) ≤ 0;
б) (х - 2)³ х² (х + 1) > 0;
в)  ; г) ; г)  .
2. Пусть f(x) = x²(x - 3).
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство: .
2. Пусть f(x) = x²(x - 3).
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство:
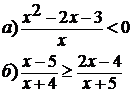 4. Найдите область допустимых значений функции:
4. Найдите область допустимых значений функции:
 5. Пусть f(x) =
5. Пусть f(x) = 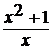 .
Найдите все х, удовлетворяющ. условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0; .
Найдите все х, удовлетворяющ. условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0;
| Метод интервалов. В. 2.
1. Решить неравенство:
а) (х - 2)(х + 5) ≥ 0;
б) (х - 3)² х³ (х + 2) < 0;
в)  ; г) ; г) 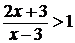 .
2. Пусть f(x) = x(x + 2)².
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство: .
2. Пусть f(x) = x(x + 2)².
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство:
 4. Найдите область допустимых значений функции:
4. Найдите область допустимых значений функции:
 5. Пусть f(x) =
5. Пусть f(x) =  Найдите все х, удовлетворяющие условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0;
Найдите все х, удовлетворяющие условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0;
|
Метод интервалов. В. 3.
1. Решить неравенство:
а) (х - 1)(х + 2) ≤ 0;
б) (х - 5)³ х4 (х + 1) > 0;
в)  ;г) ;г)  .
2. Пусть f(x) = 2x(x + 3)².
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство: .
2. Пусть f(x) = 2x(x + 3)².
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство:
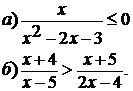 4. Найдите область допустимых значений функции:
4. Найдите область допустимых значений функции:
 5. Пусть f(x) =
5. Пусть f(x) =  . Найдите все х, удовлетворяющ. условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0; . Найдите все х, удовлетворяющ. условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0;
| Метод интервалов. В. 4.
1. Решить неравенство:
а) (х - 6)(х + 5) ≥ 0;
б) (х - 3)4 х³ (х + 4) < 0;
в) 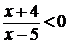 ; г) ; г)  .
2. Пусть f(x) =7x²(x - 2).
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство: .
2. Пусть f(x) =7x²(x - 2).
Найдите те значения х, для которых: а) f(x) > 0;
б) f(x) < 0; в) f(x) ≥ 0;
г) f(x) ≤ 0.
3. Решить неравенство:
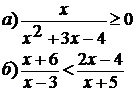 4. Найдите область допустимых значений функции:
4. Найдите область допустимых значений функции:
 5. Пусть f(x) =
5. Пусть f(x) =  Найдите все х, удовлетворяющие условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0;
Найдите все х, удовлетворяющие условию:
а) f′(x) > 0; б) f′(x) < 0;
в) f′(x) = 0;
|
Не нашли, что искали? Воспользуйтесь поиском: