Совершенная конъюнктивная нормальная форма.

Конъюнктивной нормальной формой (КНФ) называется форма представления функции в виде конъюнкции ряда членов, каждый из которых является простой дизъюнкцией аргументов (или их инверсий).

Примером КНФ может служить следующая форма представления функции:

.

Приведем формы представления функций, не являющиеся КНФ:

(здесь третий член не является простой дизъюнкцией аргументов или их инверсий);

.

(эта форма также не является КНФ, так как в ней первый член не увязан с остальными операцией конъюнкции).

В совершенной конъюнктивной нормальной форме (СКНФ) в каждом члене КНФ должны быть представлены все аргументы или их инверсии.

Для перехода от КНФ к СКНФ необходимо добавить к каждому члену, не содержащему всех аргументов, члены вида , где x_i – аргумент, не представленный в члене. Так как , то такая операция не может изменить значение функции.

Добавление к некоторому члену функции Y = f(x₁,x₂,x₃) образует выражение вида , которое можно привести к виду:

.

Справедливость данного равенства вытекает из распределительного закона, она может быть показана также путем раскрытия скобок в правой части выражения:

,

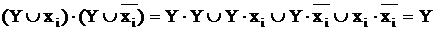так как Y·Y = Y; ; .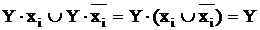

Рассмотрим переход от КНФ к СКНФ на примере функции

В первую очередь добавим в каждую дизъюнкцию недостающие аргументы:

Обзаведемся черновиком и применим распределительный закон к выражению в первых скобках. Сделав замену переменных и обозначив , получим:

Проведя обратную замену, подставим вместо Y замененное выражение:

.

Для дальнейшего преобразования сделаем еще две замены: и , и вновь применим распределительный закон:

.

Подставив сюда значения z₁ и z₂ и упорядочив переменные в дизъюнкциях, получим соответствующие члены приведенного выше выражения при переходе от КНФ к СКНФ:

Обозначив 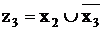, аналогично преобразуем выражение во второй скобке и добавим результат к полученному ранее выражению:

Учитывая, что 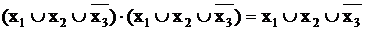приведем подобные члены и получим окончательную запись СКНФ:

Совершенная КНФ легко строится по таблице истинности. Рассмотрим в качестве примера функцию, таблица истинности которой приведена выше в таблице 1. СКНФ этой функции имеет вид:

.

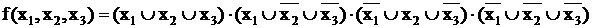Выражение содержит столько членов, связанных операцией конъюнкции сколько нулей имеется среди значений функции f(x₁,x₂,x₃) в таблице истинности. Таким образом, каждому набору значений аргументов, при котором значение функции равно нулю, соответствует определенный член СКНФ, принимающий при этом наборе значение нуль. Так как члены СКНФ связаны операцией конъюнкции, при обращении в нуль одного из членов и вся функция оказывается равной нулю.

Таким образом, можно сформулировать следующее правило записи СКНФ функции, заданной таблицей истинности.

Следует записать столько конъюнктивных членов, представлявших собой дизъюнкции всех аргументов, при скольких наборах значений аргументов функция равна нулю, и если в наборе значение аргумента равно единице, то в дизъюнкцию входит инверсия этого аргумента. Любая функция имеет единственную СКНФ.

Структурная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Недостаток такого метода построения структурных схем, обеспечивающего, в общем, правильное функционирование устройства, состоит в том, что получающиеся схемы, как правило, оказываются неоправданно сложными, требуют использования большого числа логических элементов и, следовательно, имеют низкие экономичность и надежность.

Во многих случаях удается так упростить логическое выражение, не нарушая функции, что соответствующая структурная схема оказывается существенно более простой. Рассмотрим один из методов (называемых методами минимизации логических функций) такого упрощения функции.

Не нашли, что искали? Воспользуйтесь поиском: