Упрощение логических функций.

Карта Карно. Наиболее распространенным способом минимизации СДНФ и СКНФ логической функции является выполнение преобразований, аналогичных преобразованиям обычной алгебры. Это возможно, поскольку для операций «И» и «ИЛИ» справедливы законы ассоциативности (сочетательный) и дистрибутивности (распределительный). Другими словами, аргументы можно группировать, а общие аргументы – выносить за скобки. Речь идёт о том, чтобы перейти от СДНФ к ДНФ с минимумом слагаемых, при этом количество множителей в каждом слагаемом должно быть также минимальным (избавиться от «совершенства»), то есть максимально уменьшить количество переменных и операций в СДНФ. Целью минимизации логической функции в строгом понимании этого термина является нахождение минимальной ДНФ или одной из минимальных ДНФ, если их несколько.

Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

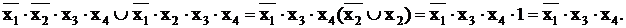
Аналогично для КНФ:

В отличие от единственных существующих СДНФ и СКНФ, ДНФ и КНФ может быть несколько. Какого-либо правила группировки, гарантированно приводящего любую ДНФ и КНФ к её минимальной форме (которых тоже может быть несколько), не существует. Приходится пробовать различные варианты и сравнивать результаты, что для больших форм может оказаться достаточно сложной задачей. Карты Карно – это наглядный способ отыскания таких термов. Перестроенную соответствующим образом таблицу истинности функции, представленную картой Карно, можно рассматривать как определенную плоскую развертку n-мерного булева куба.

Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.

В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом. Благодаря использованию кода Грея, верхняя строка карты Карно является соседней с нижней, а правый столбец соседний с левым.

Если представить объемный образ, то нетрудно заметить, что при n = 2 (функция от двух переменных) карта Карно имеет размерность 2 х 2 и ничего соединять не надо. Такой функции соответствует 2-мерный куб (квадрат). Заполняя карту, запишем в заголовки столбцов возможные формы (аргументы или их инверсии) аргумента , а в подписи строк формы аргумента .Например, для функции , записанной в СДНФ карта Карно принимает вид

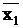
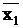
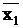
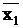
f

На карте 2 х 4 нужно соединять только 2 грани (строки соединять не надо) – получаем цилиндр (см. рис. 1).

Рис. 2. Первый и последний столбец являются соседними

На карте 4 x 4 соединяются и строки, и столбцы – получается тор. Приводя примером этой геометрической фигуры бублик, следует понимать, что карта Карно представляет только его поверхность, а не весь объем.

Рис. 3. Крайние строки и столбцы являются соседними

На карте 4 х 8 склеиваем поэлементно квадраты 4 х 4 и получаем телесный тор (толстый шланг, скрученный в тор). Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки.

На карте 8х8 - склеиваем поэлементно квадраты 4 х 4 в вертикальной и в горизонтальной плоскости – получаем телесный тор (толстый шланг, скрученный в тор), каждая точка которого имеет свой (самостоятельный) цвет, разлагаемый в ряд Фурье (без цвета в трехмерное пространство данный объект не вписывается).

С получаемыми торами нужно быть осторожнее. Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти.

Подробная информация по теме занятия размещена в электронных учебниках (Lessons и «Медицинская информатика»)

Не нашли, что искали? Воспользуйтесь поиском: