Теоретические основы. С помощью логических переменных и символов логических операций любое высказывание можно формализовать

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Логическая формула - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).

Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

Пример. – логическая функция двух переменных A и B.

Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности.

Приведем таблицу истинности основных логических операций (табл. 2)

Таблица 2

A	B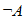

Опираясь на данные таблицы истинности основных логических операций можно составлять таблицы истинности для более сложных формул.

Алгоритм построения таблиц истинности для сложных выражений:

1. Определить количество строк:

• количество строк = 2ⁿ + строка для заголовка,
• n - количество простых высказываний.

2. Определить количество столбцов:

• количество столбцов = количество переменных + количество логических операций;
• определить количество переменных (простых выражений);
• определить количество логических операций и последовательность их выполнения.

Пример 1. Составить таблицу истинности для формулы И–НЕ, которую можно записать так: .

1. Определить количество строк:

На входе два простых высказывания: А и В, поэтому n=2 и количество строк =2²+1=5.

2. Определить количество столбцов:

Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4.

3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 3).

Таблица 3. Таблица истинности для логической операции

A	B

Подобным образом можно составить таблицу истинности для формулы ИЛИ–НЕ, которую можно записать так:

.

Таблица 4. Таблица истинности для логической операции

A	B

Примечание: И–НЕ называют также «штрих Шеффера» (обозначают |) или «антиконъюнкция»; ИЛИ–НЕ называют также «стрелка Пирса» (обозначают ↓) или «антидизъюнкция».

Пример 2. Составить таблицу истинности логического выражения .

Решение:

1. Определить количество строк:

На входе два простых высказывания: А и В, поэтому n=2 и количество строк=2²+1= 5.

2. Определить количество столбцов:

Выражение состоит из двух простых выражений (A и B) и пяти логических операций (2 инверсии, 2 конъюнкции, 1 дизъюнкция), т.е. количество столбцов таблицы истинности = 7.

Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.

3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 5).

Таблица 5. Таблица истинности для логической операции

A	B		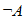			C

Практическое задание

1. Определить тождественно истинность формулы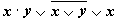

2. Определить тождественно ложность формулы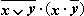

3. Являетсяформула выполнимой.

Контрольные вопросы

1.Понятие логической формулы.

2. Понятие логической функции.

3.Таблицы истинности основных логических функций.

Список литературы

Не нашли, что искали? Воспользуйтесь поиском: