
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теоретические основы. Элементы математической логики
Элементы математической логики
Логика высказываний
Высказыванием называется повествовательное предложение, о котором можно сказать в данный момент, что оно истинно или ложно, но не то и другое одновременно. Истинность или ложность предложения есть истинное значение высказывания. Сопоставим каждому высказыванию переменную равную 1, если оно истинно и равную 0 если оно ложно. Если P и Q – некоторые высказывания, то можно образовать высказывания “P или Q”, “P и Q”, “не P”, введя операции дизъюнкции (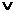 ), конъюнкции(&) и отрицания. Действия этих операций задаются таблицами истинности (таб. 1-3), каждой строке которых взаимно однозначно соответствуют набор значений составляющих высказываний и соответствующее значение составного высказывания.
), конъюнкции(&) и отрицания. Действия этих операций задаются таблицами истинности (таб. 1-3), каждой строке которых взаимно однозначно соответствуют набор значений составляющих высказываний и соответствующее значение составного высказывания.
Таблица 1 Таблица 2 Таблица 3
| P | Q | P 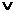 Q Q
| P | Q | P&Q | P | 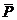
| ||
Операции дизъюнкции, конъюнкции и отрицания читаются как «или», «и» и «не».
Приведем основные законы, определяющие эти операции:
закон идемпотентности дизъюнкции и конъюнкции
 (1)
(1)
закон коммутативности дизъюнкции и конъюнкции
 (2)
(2)
закон ассоциативности дизъюнкции и конъюнкции
 (3)
(3)
закон дистрибутивности конъюнкции относительно дизъюнкции и дизъюнкции относительно конъюнкции
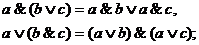 (4)
(4)
закон двойного отрицания
 (5)
(5)
законы де Моргана
 (6)
(6)
законы склеивания
 (7)
(7)
законы поглощения
 (8)
(8)
законы Порецкого
 (9)
(9)
Законы, определяющие действия с константой
 (10)
(10)
Всякое высказывание, построенное с помощью операций «и», «или», «не», имеет некоторое истинное значение, зависящее от значений составляющих высказываний. Любое высказывание f может быть задано в виде таблицы истинности. Если значение высказывания зависит от n составляющих высказываний x1,x2,x3,…xn, то таблица истинности содержит 2 n строк. Составляющие высказывания xi будем называть атомарными высказываниями или просто переменными xi, рассматривая при этом сложное высказывание как функцию f от n переменных.
Построение совершенных нормальных форм.
Исчисление высказываний можно построить используя соответствующие таблицы истинности. Алгебра Буля простейшая в классе булевых алгебр; она является двухэлементной булевой алгеброй. Одним из элементов двухэлементной булевой алгебры является 0, так как булева алгебра является решеткой с дополнениями, поэтому вторым элементом этой алгебры является 1.
Каждое высказывание и соответствующую ему булеву функцию f (x1,x2,…xn) можно представить в виде дизъюнкции конституент 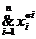 , где
, где
 .
.
Пример 1. Рассмотрим пример высказывания f(x1,x2,x3), заданное таблицей истинности (таб. 4)
Таблица 4.
| x1 | X2 | x3 | f(x1,x2,x3) | x1 | x2 | x3 | f(x1,x2,x3) | |
Согласно предыдущему утверждению функция f(x1,x2,x3) может быть представлена в виде:
f(x1,x2,x3)=  .
.
В дальнейшем представление булевой функции f(x1,x2…xn) в виде дизъюнкции конституент будем называть совершенной дизъюнктивной нормальной формой (СДНФ) функции f(x1,x2…xn).
Переменную или ее отрицание будем называть первичным термом. Количество первичных термов, которые образуют форму, называют сложностью L(f) этой формы.
Сложность СДНФ функции из примера равна 12. Для уменьшения сложности этой функции используют основные тождества алгебры Буля (законы 1-8). Согласно свойству идемпотентности дизъюнкции имеем:
f(x1,x2,x3)=  .
.
Используя свойства коммутативности, ассоциативности и дистрибутивности, получаем:
f(x1,x2,x3)= 
Окончательно имеем
f(x1,x2,x3)= 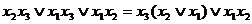
В результате получаем сложность L(f) функции f(x1,x2,x3) равную 5.
Аналогично можно каждое высказывание и соответствующую ему булеву функцию f (x1,x2,…xn) представить в виде конъюнкции конституент  , где
, где
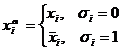 .
.
В дальнейшем представление булевой функции f(x1,x2…xn) в виде конъюнкции дизъюнкций будем называть совершенной конъюнктивной нормальной формой (СКНФ) функции f(x1,x2…xn).
Для примера 1 функция f(x1,x2,x3) может быть представлена в виде:
f(x1,x2,x3)= 
Булевы функции двух переменных
Любое сложное высказывание можно представить в виде выражения, в которое входят простые высказывания (переменные) xi операции дизъюнкции, конъюнкции, отрицания и, быть может, скобки. Рассмотрим, каким свойствам должны удовлетворять операции, с помощью которых можно выражать любое сложное выражение.
Суперпозицией системы
 называется любая функция f, полученная:
называется любая функция f, полученная:
а) из 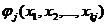 переименованием переменных,
переименованием переменных,  ;
;
б) подстановкой вместо некоторых переменных функции  функций
функций  ,
,  ;
;
в) с помощью многократно применения пунктов а) и б).
Система S называется полной в Pk, если любая функция f  Pk представима в виде суперпозиции этой системы; система S называется базисом, если полнота S теряется при удалении хотя бы одной функции, где Pk – k-значная логика.
Pk представима в виде суперпозиции этой системы; система S называется базисом, если полнота S теряется при удалении хотя бы одной функции, где Pk – k-значная логика.
Построим все булевы функции от двух переменных (таб.5)
Таблица5
| переменные | Булевы функции | ||||||||||||||||
| x1 | x2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
Индекс i функциональной переменной fi, i=0,1,2,….,15, равен десятичному эквивалентному набору значений этой функции, читаемой сверху вниз. Приведем эти булевы функции:
f0(x1,x2)=0 – константа 0;
f1(x1,x2)=  конъюнкция;
конъюнкция;
f2(x1,x2)=  - левая коимпликация (читается «не если x1, то x2);
- левая коимпликация (читается «не если x1, то x2);
f3(x1,x2)= 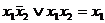 ;
;
f4(x1,x2)= 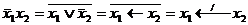 - правая коимпликация;
- правая коимпликация;
f5(x1,x2)= 
f6(x1,x2)=  - сложение по модулю 2 или функция неравнозначности, неэквивалентности;
- сложение по модулю 2 или функция неравнозначности, неэквивалентности;
f7(x1,x2)= 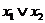 - дизъюнкция;
- дизъюнкция;
f8(x1,x2)= 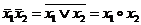 - функция Вебба;
- функция Вебба;
f9(x1,x2)=  - функция эквивалентности, равнозначности;
- функция эквивалентности, равнозначности;
f10(x1,x2)=  - отрицание;
- отрицание;
f11(x1,x2)=  - правая импликация (читается «если x2, то x1);
- правая импликация (читается «если x2, то x1);
f12(x1,x2)= 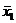 - отрицание;
- отрицание;
f13(x1,x2)=  левая импликация (читается «если x1, то x2);
левая импликация (читается «если x1, то x2);
f14(x1,x2)=  - функция Шеффера;
- функция Шеффера;
f15(x1,x2)=1– константа 1.
Не нашли, что искали? Воспользуйтесь поиском: