Метод покоординатного спуска.

Метод покоординатного спуска применяется для решения экстремальных задач, в которых целевая функция либо не обладает нужной гладкостью, либо является гладкой, но вычисление производных слишком трудоемко. В таких случаях желательно иметь методы решения, которые используют лишь значения функции. Далее приводится описание метода покоординатного спуска для следующей задачи:

Пусть e_i=(0,…,0,1,0,…,0) – i -ый единичный координатный вектор, x⁰ – начальное приближение, a₀ > 0 – начальная длина шага. Пусть x^k ϵ Rⁿ – текущее приближение, a_k > 0 – текущая длина шага, λ ϵ (0,1) – фиксированное число.

Метод покоординатного спуска – итеративный процесс. На каждой итерации метода в качестве направления спуска используется один из единичных координатных векторов. Так как таких векторов ровно n, то множество всех итераций естественно разбивается на группы из n итераций. Занумеруем итерации так, чтобы t -ая группа начиналась с итерации с номером (t-1)n+1, а последняя итерация этой группы заканчивалась номером tn.

Опишем итерацию с номером k, где

(t-1)n+1 ≤ k ≤ tn.

Сначала проверяется можно ли улучшить текущее приближение, сдвигаясь в направлении координатного вектора e_k-(t-1)n с длиной шага a_k-1. Если удается улучшить значение целевой функции

то пересчитывается текущее приближение по формулам

В противном случае проверяется вектор -e_k-(t-1)n. Если выполняется неравенство

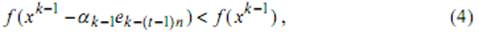
Тогда

Если выполняется (2) или (4), то будем говорить, что итерация k удачная. В случае неудачной итерации k положим x^k=x^k-1,

Пусть в t -ой группе не оказалось ни одной удачной итерации и шаг дробится. В этом случае выполняются неравенства

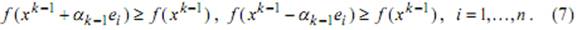
Если в данной группе из n итераций реализовалась хотя бы одна удачная итерация, то тогда на последней итерации группы длина шага не дробится и сохраняется еще на протяжении n итераций следующего цикла, так как дробление возможно только на последней итерации цикла.

Не нашли, что искали? Воспользуйтесь поиском: