Метод случайного поиска. Алгоритм с возвратом при неудачном шаге.

Основная особенность этого метода состоит в том, что в процессе вычисления приближений x^k используются случайные вектора в качестве направления движения. Например,

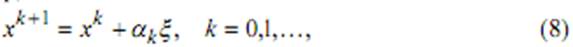
где a_k > 0 – длина шага, – реализация n -мерной случайной величины ξ с заданным распределением. Например, ξ_i – независимые случайные величины, равномерно распределенные на отрезке [-1,1]. Таким образом, любая реализация метода случайного поиска использует генератор случайных чисел, который по любому запросу выдает реализацию случайного вектора ξ с заданной функцией распределения.

Рассмотрим задачу 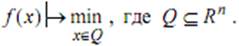Пусть известно k -ое приближение x^k ϵ Q, k = 0,1,…. Далее приводится описание нескольких вариантов метода случайного поиска.

Алгоритм с возвратом при неудачном шаге

Идея этого алгоритма заключается в следующем. На каждом шаге берется некоторая реализация случайной величины ξ и вычисляется вектор v^k=x^k+aξ, где a=const > 0 – длина шага. Если v^k ϵ Q и f(v^k) < f(x^k), то предлагаемый шаг считаем удачным. В этом случае x^k+1=v^k. Если v^k ϵ Q, f(v^k) ≥ f(x^k), или v^k ϵ Q, то шаг является неудачным, тогда полагаем x^k+1=x^k. Если на текущей итерации оказывается, что x^k=x^k+1=…=x^k+N для достаточно большого N, то алгоритм останавливается и x^k является искомым приближением.

Не нашли, что искали? Воспользуйтесь поиском: