Градиентный метод. Метод с дроблением шага.

В этом варианте градиентного метода величина шага 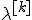на каждой итерации выбирается из условия выполнения неравенства 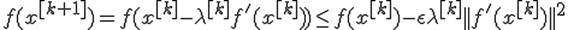(2)

где - 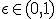некоторая заранее выбранная константа.

Процедуру нахождения такого 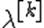обычно оформляют так. Выбирается число 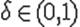и некоторый начальный шаг 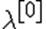. Теперь для каждого k полагают 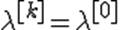и делают шаг градиентного метода. Если с таким 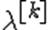условие (2) выполняется, то переходят к следующему k. Если же (2) не выполняется, то умножают 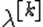на 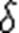("дробят шаг") и повторяют эту процедуру до тех пор пока неравенство (2) не будет выполняться. В условиях теоремы 1 эта процедура для каждого k за конечное число шагов приводит к нужному .

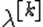Можно показать, что в условиях теоремы 2 градиентный метод с дроблением шага линейно сходится. Описанный алгоритм избавляет нас от проблемы выбора 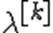на каждом шаге, заменяя ее на проблему выбора параметров 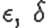и 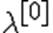, к которым градиентный метод менее чувствителен. При этом, разумеется, объем вычислений возрастает (в связи с необходимостью процедуры дробления шага), впрочем, не очень сильно, поскольку в большинстве задач основные вычислительные затраты ложатся на вычисление градиента.

Не нашли, что искали? Воспользуйтесь поиском: