Численные методы решения задач линейного программирования. Прямой симплекс-метод. Алгоритм симплекс-метода.

Сформулируем симплекс-метод в виде следующей последовательности шагов.

Шаг 0. Построить симплекс-таблицу, соответствующую заданному базисному допустимому решению, таблица будет прямо допустимой.

Шаг 1. Если симплекс-таблица двойственно допустима, то КОНЕЦ (получено оптимальное решение).

Шаг 2. Иначе выбрать ведущий столбец s по правилу:

Шаг 3. Если , то выбрать ведущую строку r по правилу:

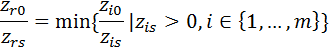
иначе КОНЕЦ (задача неразрешима из-за неограниченности целевой функции).

Шаг 4. Преобразовать симплекс-таблицу, положить q (r):= s и перейти на шаг 1.

Шаги с 1-го по 4-ый образуют одну итерацию симплекс-метода. Обоснование шага 1 содержится в лемме 4, а шага 3 – в леммах 5 и 6. Из доказательства леммы 6 также следует, что при элементарном преобразовании сохраняется прямо допустимость симплекс-таблицы.

В данном алгоритме не описан 0-ой шаг, а именно, способ построения начальной симплекс-таблицы. Предполагается, что известно начальное б.д.р.

Реализация 0-го шага содержится в параграфе 4 при описании двухфазного симплекс-метода.

При выполнении шагов 2 и/или 3 выбор ведущего столбца s и/или ведущей строки r может оказаться неоднозначным. Существуют разные правила выбора ведущего элемента. Ограничимся теми правилами, которые приводят к детерминированному алгоритму решения задач ЛП.

При выборе ведущего столбца используются следующие способы:

а) правило Данцига, которое заключается в выборе s с минимальным z0s < 0;

б) правило Блэнда, которое состоит в выборе наименьшего s такого, что z0s < 0.

При выборе ведущей строки используются следующие способы:

а) правило Блэнда: выбрать строку r с минимальным номером базисной переменной q (r), удовлетворяющей условиям шага 3;

б) лексикографическое правило, описанное в параграфе 3: выбрать строку r, для которой вектор лексикографически минимален среди векторов

Не всегда выбор ведущего элемента можно свести к последовательному выбору сначала ведущего столбца, а затем ведущей строки. Примером является правило наибольшего улучшения, в котором требуется выбрать такой ведущий элемент, для которого достигается максимальное уменьшение целевой функции.

Не нашли, что искали? Воспользуйтесь поиском: