Численные методы решения задач линейного программирования. Геометрическая интерпретация задач линейного программирования

Приведем геометрическую интерпретацию задач линейного программирования применительно к следующей паре взаимодвойственных задач, которые обозначим, соответственно, через P и D:

Обозначим через , расширенные вектор-столбцы матрицы А, а через – расширенный вектор правых частей ограничений прямой задачи. Множество K, содержащее с любой своей точкой x все точки при , называется конусом.

Определим линейное преобразование:

Пусть Очевидны следующие свойства множества K:

1. K – выпуклый конус.

2. Вектор и является его вершиной.

3. K порожден конечным числом векторов то есть является множеством точек вида

Чтобы пояснить введенное определение конуса K, рассмотрим следую-щую задачу линейного программирования:

На рисунке приведено множество K для данной задачи. Очевидно, что конус K порожден крайними лучами, образованными векторами Рассмотрим систему уравнений:

Будем считать, что вектор c коэффициентов целевой функции прямой задачи P не является линейной комбинацией векторов , так как в противном случае любое допустимое решение является оптимальным. Тогда

Обозначим последнее множество через Q. Оно является прямой в пространстве , которая проходит через точку параллельно оси

то образом множества допустимых решений задачи P при отображении является пересечение конуса K и прямой Q. Таким образом, задача P сводится к поиску «крайней» точки пересечения прямой Q и конуса K, то есть точки с наименьшей последней координа-той.

На рис. 2 точка M – крайняя точка пересечения 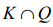, является образом оптимальных решений рассмотренной выше задачи ЛП. Приведем интерпретацию задачиD. Пусть

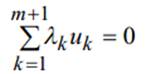
уравнение гиперплоскости, проходящей через начало координат. Направ-ляющий вектор гиперплоскости определен с точностью до ненулевого множителя. Будем считать, что . Другими словами, мы не рассматриваем гиперплоскости содержащие ось 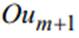. Следовательно, существует взаимнооднозначное соответствие между гиперплоскостями,

проходящими через ноль, не содержащими ось , и их направляющими векторами . Пусть – допустимое решение задачи D, а – гиперплоскость, определяемая уравнением

Подставим в это уравнение. Так как y является допустимым решением задачи D, то 0

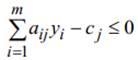. Поскольку конус K порожден векторами , K ле-жит «над» гиперплоскостью 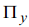, то есть по ту же сторону от гиперплоскости, что и векто

Пусть 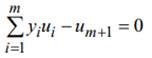– произвольная гиперплоскость, проходящая че-рез O и не содержащая ось . Если конус K располагается «над» ги-перплоскостью, то есть для любой точки справедливо , тогда для любого расширенного вектора условий выполняется 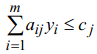, следовательно, является допустимым

решением задачи D. Итак, геометрическим образом множества допустимых решений задачи D является совокупность гиперплоскостей, содержащих начало координат, не содержащих ось и расположенных «под» конусом K. Это соответст-вие является взаимнооднозначным и определяется уравнениями (21).

Пусть . Тогда из определенияQ и (21) имеем

Следовательно, значение целевой функции двойственной задачи на допустимом решении равно расстоянию от точки пересечения прямойQ и гиперплоскости 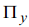до гиперплоскости

Таким образом, с геометрической точки зрения двойственная задача заключается в отыскании такой гиперплоскости, которая содержит начало координат, не содержит ось , расположена «под» конусом K и пересекает Q в «наивысшей точке» в смысле порядка на оси .

Не нашли, что искали? Воспользуйтесь поиском: